Barycentriske koordinater

Barycentriske koordinater er tripler af tal svarende til masser placeret på hjørnerne af en referencetrekant . Disse masser bestemmer derefter et punkt , som er de tre massers geometriske centroid og identificeres med koordinaterne . Trekantens hjørner er givet ved , , og . Barycentriske koordinater blev opdaget af Möbius i 1827 (Coxeter 1969, s. 217; Fauvel et al. 1993).

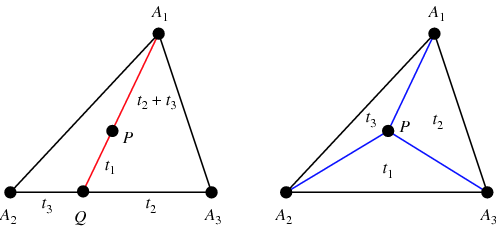
For at finde de barycentriske koordinater for et vilkårligt punkt skal man finde og fra punktet i skæringspunktet mellem linjen og siden , og bestem derefter som den masse i , der vil balancere en masse i , således at er centrum (venstre figur). Endvidere er arealerne af trekanterne , og proportionale med de barycentriske koordinater , og af (højre figur; Coxeter 1969, p. 217).

Barycentriske koordinater er homogene, så

(1)

for .

Barycentriske koordinater normaliseret således at de bliver de faktiske arealer af undertrekanterne kaldes homogene barycentriske koordinater. Barycentriske koordinater normaliseret således, at

(2)

så at koordinaterne giver arealerne af undertrekanterne normaliseret med arealet af den oprindelige trekant kaldes areal-koordinater (Coxeter 1969, s. 218). Barycentriske og areal-koordinater kan give særligt elegante beviser for geometriske sætninger som Rouths sætning, Cevas sætning og Menelaos’ sætning (Coxeter 1969, s. 219-221).

(Ikke nødvendigvis homogene) barycentriske koordinater for en række almindelige centre er opsummeret i følgende tabel. I tabellen er , og sidelængderne i trekanten, og er dens semiperimeter.

trekantens centrum	barycentriske koordinater
omkredscentrum	(, , )
excenter
excenter
excenter
Gergonne punkt Ge	(, , )
incenter
Nagelpunkt Na
orthocenter	(, , )
symmedianpunkt
trekantcentrum

I barycentriske koordinater har en linje en lineær homogen ligning. Især har linjen, der forbinder punkterne og , ligning

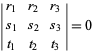(3)

(Loney 1962, pp. 39 og 57; Coxeter 1969, s. 219; Bottema 1982). Hvis toppene i en trekant har barycentriske koordinater , så er trekantens areal

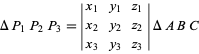(4)

(Bottema 1982, Yiu 2000).