Disse er stokastiske læringsprocesser med tilbagevendende struktur og er grundlaget for de tidlige optimeringsteknikker, der anvendes i ANN. Boltzmann-maskinen blev opfundet af Geoffrey Hinton og Terry Sejnowski i 1985. Hintons ord om Boltzmann Machine giver større klarhed.
“Et overraskende træk ved dette netværk er, at det kun anvender lokalt tilgængelige oplysninger. Ændringen af vægten afhænger kun af adfærden hos de to enheder, den forbinder, selv om ændringen optimerer et globalt mål.” – Ackley, Hinton 1985.
Nogle vigtige punkter om Boltzmann Machine –
-
De anvender tilbagevendende struktur.
-
De består af stokastiske neuroner, som har en af de to mulige tilstande, enten 1 eller 0.
-
Nogle af neuronerne i dette er adaptive (fri tilstand), og nogle er fastklemte (frossen tilstand).
-
Hvis vi anvender simuleret udglødning på diskrete Hopfield-netværk, vil det blive til Boltzmann-maskine.
Objektet med Boltzmann-maskinen
Det vigtigste formål med Boltzmann-maskinen er at optimere løsningen af et problem. Det er Boltzmann-maskinens arbejde at optimere de vægte og den mængde, der er relateret til det pågældende problem.
Arkitektur
Det følgende diagram viser arkitekturen i Boltzmann-maskinen. Det fremgår tydeligt af diagrammet, at der er tale om et todimensionalt array af enheder. Her er vægtene på sammenkoblinger mellem enhederne -p, hvor p > 0. Vægtene på selvforbindelser er givet ved b, hvor b > 0.
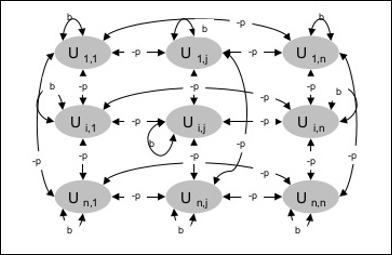
Træningsalgoritme
Som vi ved, at Boltzmann-maskiner har faste vægte, vil der derfor ikke være nogen træningsalgoritme, da vi ikke behøver at opdatere vægtene i netværket. For at teste netværket skal vi imidlertid indstille vægtene samt finde konsensusfunktionen (CF).
Boltzmann-maskine har et sæt enheder Ui og Uj og har tovejsforbindelser på dem.
-
Vi betragter den faste vægt sige wij.
-
wij ≠ 0, hvis Ui og Uj er forbundet.
-
Der findes også en symmetri i den vægtede sammenkobling, dvs.dvs. wij = wji.
-
wii eksisterer også, dvs. der vil være selvforbindelse mellem enheder.
-
For enhver enhed Ui vil dens tilstand ui enten være 1 eller 0.
Det vigtigste mål for Boltzmann-maskinen er at maksimere konsensusfunktionen (CF), som kan gives ved følgende relation
$$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$$
Nu, når tilstanden ændres fra enten 1 til 0 eller fra 0 til 1, kan ændringen i konsensus være givet ved følgende relation –
$$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$$
Her ui er den aktuelle tilstand for Ui.
Variationen i koefficienten (1 – 2ui) er givet ved følgende relation –
$$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:er\:aktuelt\:off\\\-1, & U_{i}\:is\:currently\:on\end{cases}$$$$
Generelt set ændrer enhed Ui ikke sin tilstand, men hvis den gør det, vil informationen blive opbevaret lokalt for enheden. Med denne ændring vil der også ske en stigning i netværkets konsensus.
Sandsynligheden for, at netværket accepterer ændringen i enhedens tilstand, er givet ved følgende relation –
$$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$$
Her er T den styrende parameter. Den vil falde, når CF når den maksimale værdi.
Testalgoritme
Strin 1 – Initialiser følgende for at starte træningen –
- Vægte, der repræsenterer problemets begrænsning
- Kontrolparameter T
Strin 2 – Fortsæt trin 3-8, når stopbetingelsen ikke er sand.
Strin 3 – Udfør trin 4-7.
Strin 4 – Antag, at en af tilstanden har ændret vægten, og vælg det hele tal I, J som tilfældige værdier mellem 1 og n.
Strg 5 – Beregn ændringen i konsensus på følgende måde –
$$$\\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$$
Stræk 6 – Beregn sandsynligheden for, at dette netværk vil acceptere ændringen i tilstanden
$$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$$
Strg 7 – Accepter eller afvis denne ændring på følgende måde –
Fald I – hvis R < AF, accepter ændringen.
Fald II – hvis R ≥ AF, afvis ændringen.
Her er R et tilfældigt tal mellem 0 og 1.
Strin 8 – Reducer kontrolparameteren (temperatur) som følger –
T(ny) = 0.95T(gammel)
Stræk 9 – Test for stopbetingelserne, som kan være som følger –
- Temperaturen når en bestemt værdi
- Der sker ingen ændring i tilstanden i et bestemt antal iterationer