Biografi

Brahmagupta (598-668 e.Kr.)
Den store indiske matematiker og astronom Brahmagupta fra det 7. århundrede skrev nogle vigtige værker om både matematik og astronomi. Han var fra staten Rajasthan i det nordvestlige Indien (han omtales ofte som Bhillamalacarya, læreren fra Bhillamala), og senere blev han leder af det astronomiske observatorium i Ujjain i det centrale Indien. De fleste af hans værker er skrevet på elliptiske vers, en almindelig praksis i indisk matematik på den tid, og har derfor noget af en poetisk klang.
Det er sandsynligt, at Brahmaguptas værker, især hans mest berømte tekst, “Brahmasphutasiddhanta”, blev bragt af den abbasidiske kalif Al-Mansur i det 8. århundrede til hans nyoprettede læringscenter i Baghdad på bredden af Tigris, hvilket var en vigtig forbindelse mellem indisk matematik og astronomi og den begyndende opblomstring af videnskab og matematik i den islamiske verden.
I sit værk om aritmetik forklarede Brahmagupta, hvordan man finder kubikken og kubikroden af et helt tal og gav regler, der gjorde det lettere at beregne kvadrater og kvadratrødder. Han gav også regler for håndtering af fem typer af kombinationer af brøker. Han angav summen af kvadraterne af de første n naturlige tal som n(n + 1)(2n + 1)⁄ 6 og summen af terningerne af de første n naturlige tal som (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Behandle nul som et tal

Brahmagupta’s regler for håndtering af nul og negative tal
Brahmagupta’s genialitet kom dog i hans behandling af begrebet (dengang relativt nyt) tallet nul. Selv om det ofte også tilskrives den indiske matematiker Bhaskara I fra det 7. århundrede, er hans “Brahmasphutasiddhanta” sandsynligvis den tidligst kendte tekst, der behandler nul som et selvstændigt tal og ikke blot som et stedfortræderciffer, som det blev gjort af babylonierne, eller som et symbol for manglende mængde, som det blev gjort af grækerne og romerne.
Brahmagupta opstillede de grundlæggende matematiske regler for behandling af nul (1 + 0 = 1; 1 – 0 = 1; og 1 x 0 = 0), selv om hans forståelse af division med nul var ufuldstændig (han troede, at 1 ÷ 0 = 0). Næsten 500 år senere, i det 12. århundrede, viste en anden indisk matematiker, Bhaskara II, at svaret burde være uendeligt og ikke nul (med den begrundelse, at 1 kan deles i et uendeligt antal stykker af størrelsen nul), et svar, der blev anset for korrekt i århundreder. Denne logik forklarer imidlertid ikke, hvorfor 2 ÷ 0, 7 ÷ 0 osv. også skulle være nul – den moderne opfattelse er, at et tal divideret med nul faktisk er “udefineret” (dvs. det giver ikke mening).
Brahmaguptas syn på tal som abstrakte størrelser, snarere end blot til tælling og måling, gjorde det muligt for ham at foretage endnu et stort begrebsmæssigt spring, som skulle få dybtgående konsekvenser for den fremtidige matematik. Tidligere blev summen 3 – 4 f.eks. anset for at være enten meningsløs eller i bedste fald blot nul. Brahmagupta indså imidlertid, at der kunne eksistere noget som et negativt tal, som han kaldte “gæld” i modsætning til “egenskab”. Han redegjorde for reglerne for håndtering af negative tal (f.eks. et negativt tal gange et negativt tal er et positivt tal, et negativt tal gange et positivt tal er et negativt tal osv.)
Dertil kommer, påpegede han, at kvadratiske ligninger (af typen x2 + 2 = 11, f.eks.) i teorien kunne have to mulige løsninger, hvoraf den ene kunne være negativ, fordi 32 = 9 og -32 = 9. Ud over sit arbejde med løsninger på generelle lineære ligninger og kvadratiske ligninger gik Brahmagupta endnu videre ved at overveje systemer af simultane ligninger (sæt af ligninger, der indeholder flere variabler) og løse kvadratiske ligninger med to ubekendte, noget, som ikke engang blev overvejet i Vesten før tusind år senere, da Fermat overvejede lignende problemer i 1657.
Brahmagupta’s Theorem on cyclic quadrilaterals
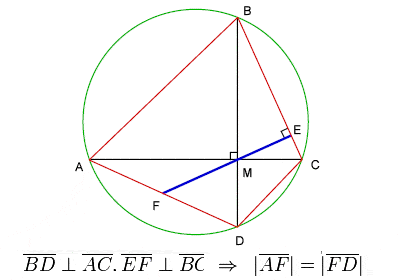
Brahmagupta’s Theorem on cyclic quadrilaterals
Brahmagupta forsøgte endda at nedskrive disse ret abstrakte begreber, ved at bruge initialerne af farvernes navne til at repræsentere ukendte i sine ligninger, en af de tidligste antydninger af det, vi nu kender som algebra.
Brahmagupta dedikerede en betydelig del af sit arbejde til geometri og trigonometri. Han etablerede √10 (3,162277) som en god praktisk tilnærmelse til π (3,141593) og gav en formel, der nu er kendt som Brahmaguptas formel, for arealet af en cyklisk firkant samt en berømt sætning om diagonalerne i en cyklisk firkant, der normalt omtales som Brahmaguptas sætning.
| << Tilbage til Indisk Matematik |
Forward to Madhava >> |