En cellulær automat er en samling af “farvede” celler på et gitter med en bestemt form, der udvikler sig gennem et antal diskrete tidstrin i henhold til et sæt regler baseret på tilstanden af nabocellerne. Reglerne anvendes derefter iterativt i så mange tidstrin som ønsket. von Neumann var en af de første, der overvejede en sådan model, og han indarbejdede en cellulær model i sin “universalkonstruktør”. Cellulære automater blev undersøgt i begyndelsen af 1950’erne som en mulig model for biologiske systemer (Wolfram 2002, s. 48). Omfattende undersøgelser af celleautomater er blevet udført af S. Wolfram fra 1980’erne, og Wolframs grundforskning på området kulminerede med udgivelsen af hans bog A New Kind of Science (Wolfram 2002), hvori Wolfram præsenterer en gigantisk samling af resultater vedrørende automater, blandt hvilke der er en række banebrydende nye opdagelser.
Afsnittet “Bettor or Worse” (2006) i sæson 2 af tv-krimien NUMB3RS nævner endimensionelle celleautomater.
Celleautomater findes i en række forskellige former og varianter. En af de mest grundlæggende egenskaber ved en cellulær automat er den type gitter, som den beregnes på. Det enkleste af disse “gitter” er en endimensional linje. I to dimensioner kan man overveje kvadratiske, trekantede og sekskantede gitre. Cellulære automater kan også konstrueres på kartesiske gitter i et vilkårligt antal dimensioner, hvor det 
-dimensionelle hele talgitter 
er det mest almindelige valg. Cellulære automater på et 
-dimensionelt heltalsgitter er implementeret i Wolfram Language som CellularAutomaton.
At antallet af farver (eller forskellige tilstande) 
en cellulær automat kan antage skal også angives. Dette antal er typisk et heltal, hvor 
(binært) er det enkleste valg. For en binær automat kaldes farve 0 almindeligvis “hvid”, og farve 1 kaldes almindeligvis “sort”. Cellulære automater, der har et kontinuerligt område af mulige værdier, kan dog også overvejes.
Ud over det gitter, som en cellulær automat lever på, og de farver, som dens celler kan antage, skal også det kvarter, som cellerne påvirker hinanden over, angives. Det enkleste valg er “nærmeste naboer”, hvor kun celler, der støder direkte op til en given celle, kan blive påvirket ved hvert tidstrin. To almindelige naboskaber i tilfælde af en todimensionel celleautomat på et kvadratisk gitter er det såkaldte Moore-naboskab (et kvadratisk naboskab) og von Neumann-naboskab (et diamantformet naboskab).
Den enkleste type celleautomat er en binær, nærmeste nabo, endimensional automat. Sådanne automater blev kaldt “elementære cellulære automater” af S. Wolfram, som har studeret deres forbløffende egenskaber indgående (Wolfram 1983; 2002, s. 57). Der findes 256 sådanne automater, som hver især kan indekseres ved hjælp af et unikt binært tal, hvis decimale repræsentation er kendt som “reglen” for den pågældende automat. En illustration af regel 30 er vist ovenfor sammen med den udvikling, den producerer efter 15 trin med udgangspunkt i en enkelt sort celle.
En lidt mere kompliceret klasse af cellulære automater er de nærmest nabo, 
-farve, endimensionelle totalistiske cellulære automater. I sådanne automater er det gennemsnittet af de tilstødende celler, der bestemmer udviklingen, og de enkleste ikke-trivielle eksempler har 
farver. For disse automater kan det regelsæt, der beskriver adfærden, indkodes som et 
-cifret 
-ary-tal, der kaldes en “kode”. Reglerne og de 300 trin i den ternære (
) kode 912 automat er illustreret ovenfor.
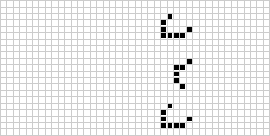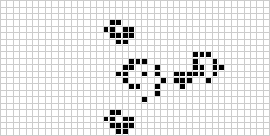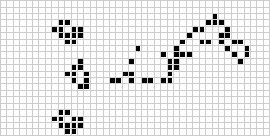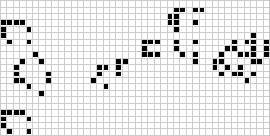
I to dimensioner er den bedst kendte celleautomat Conways livsspil, der blev opdaget af J. H. Conway i 1970 og populariseret i Martin Gardners spalter i Scientific American. Livets spil er en binær (
) totalistisk cellulær automat med et Moore-naboskab i intervallet 
. Selv om beregningen af de på hinanden følgende generationer af livets spil oprindeligt blev udført i hånden, kom computerrevolutionen snart og gjorde det muligt at studere og videreformidle mere omfattende mønstre. En animation af en game of life-konstruktion kendt som et puffer train er illustreret ovenfor.
WireWorld er en anden almindelig todimensionel cellularautomat.
Teorien om cellulære automater er uhyre rig, idet enkle regler og strukturer er i stand til at frembringe en lang række uventede adfærdsmønstre. Der findes f.eks. universelle celleautomater, som er i stand til at simulere enhver anden celleautomat eller Turing-maskine. Gacs (2001) har endda bevist, at der findes fejltolerante universelle cellulære automater, hvis evne til at simulere andre cellulære automater ikke hindres af tilfældige forstyrrelser, forudsat at sådanne forstyrrelser er tilstrækkeligt sparsomme.