Underdetermined linear system
Et underdetermined system af lineære ligninger har flere ubekendte end ligninger og har generelt et uendeligt antal løsninger. Figuren nedenfor viser et sådant ligningssystem y = D x {\displaystyle \mathbf {y} =D\mathbf {x} }

hvor vi ønsker at finde en løsning for x {\displaystyle \mathbf {x} }

.
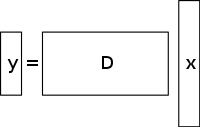
For at kunne vælge en løsning til et sådant system må man pålægge ekstra begrænsninger eller betingelser (f.eks. glathed) efter behov. Ved compressed sensing tilføjer man begrænsningen om sparsomhed, idet man kun tillader løsninger, der har et lille antal koefficienter, der ikke er nul, og som har et lille antal koefficienter, der ikke er nul. Ikke alle underdeterminerede systemer af lineære ligninger har en sparsom løsning. Hvis der imidlertid findes en unik sparsom løsning til det underdeterminerede system, kan denne løsning genfindes ved hjælp af compressed sensing-princippet.
Løsnings-/rekonstruktionsmetode

Compressed sensing udnytter redundansen i mange interessante signaler – de er ikke ren støj. Især er mange signaler sparsomme, dvs. de indeholder mange koefficienter tæt på eller lig med nul, når de repræsenteres i et eller andet domæne. Dette er den samme indsigt, der anvendes i mange former for tabsgivende komprimering.
Compressed sensing starter typisk med at tage en vægtet lineær kombination af prøver også kaldet komprimerende målinger i et andet grundlag end det grundlag, hvor signalet vides at være sparsomt. De resultater, som Emmanuel Candès, Justin Romberg, Terence Tao og David Donoho har fundet frem til, viser, at antallet af disse komprimerende målinger kan være lille og stadig indeholde næsten alle nyttige oplysninger. Derfor indebærer opgaven med at konvertere billedet tilbage til det tilsigtede domæne, at der skal løses en underbestemt matrixligning, da antallet af komprimerende målinger er mindre end antallet af pixels i det fulde billede. Hvis man tilføjer den begrænsning, at det oprindelige signal er sparsomt, kan man imidlertid løse dette underbestemte system af lineære ligninger.
Den mindste kvotes-løsning til sådanne problemer er at minimere L 2 {\displaystyle L^{2}}

norm – dvs. at minimere mængden af energi i systemet. Dette er normalt matematisk set simpelt (det involverer kun en matrixmultiplikation med pseudoinversen af den basis, der udtages prøver i). Dette fører imidlertid til dårlige resultater for mange praktiske anvendelser, for hvilke de ukendte koefficienter har en energi, der ikke er nul.
For at håndhæve sparsomhedsbegrænsningen, når man løser det underbestemte system af lineære ligninger, kan man minimere antallet af ikke-nul-komponenter i løsningen. Funktionen, der tæller antallet af ikke-nul-komponenter i en vektor, blev kaldt L 0 {\displaystyle L^{0}}

“norm” af David Donoho.
Candès et al. beviste, at det for mange problemer er sandsynligt, at L 1 {\displaystyle L^{1}}

norm er ækvivalent med L 0 {\displaystyle L^{0}}}

norm, i teknisk forstand: Dette ækvivalensresultat gør det muligt at løse L 1 {\displaystyle L^{1}}

problemet, hvilket er nemmere end L 0 {\displaystyle L^{0}}

problem. At finde den kandidat med den mindste L 1 {\displaystyle L^{1}}

norm kan relativt let udtrykkes som et lineært program, for hvilket der allerede findes effektive løsningsmetoder. Når målingerne kan indeholde en endelig mængde støj, foretrækkes basisforfølgningsafrensning frem for lineær programmering, da det bevarer sparsomhed i lyset af støj og kan løses hurtigere end et nøjagtigt lineært program.
Total variation baseret CS-rekonstruktion
Motivation og anvendelser
Rolle for TV-regularisering
Total variation kan ses som en ikke-negativ realværdifunktionel defineret på rummet af realværdifunktioner (for tilfældet med funktioner af én variabel) eller på rummet af integrerbare funktioner (for tilfældet med funktioner af flere variabler). Især for signaler henviser den samlede variation til integralet af signalets absolutte gradient. I signal- og billedrekonstruktion anvendes det som regulering af total variation, hvor det underliggende princip er, at signaler med for mange detaljer har en høj total variation, og at fjernelse af disse detaljer, samtidig med at vigtige oplysninger som f.eks. kanter bevares, vil reducere signalets totale variation og gøre signalemnet tættere på det oprindelige signal i problemet.
Med henblik på signal- og billedrekonstruktion, l 1 {\displaystyle l1}

minimeringsmodeller anvendes. Andre tilgange omfatter også de mindste kvadraters metode, som tidligere er blevet diskuteret i denne artikel. Disse metoder er ekstremt langsomme og returnerer en ikke helt perfekt rekonstruktion af signalet. De nuværende CS-regulariseringsmodeller forsøger at løse dette problem ved at indarbejde sparsomhedsprioriteter for det oprindelige billede, hvoraf en af dem er den samlede variation (TV). Konventionelle TV-tilgange er designet til at give stykvis konstante løsninger. Nogle af disse omfatter (som diskuteret længere fremme) – begrænset l1-minimisering, som anvender et iterativt skema. Selv om denne metode er hurtig, fører den efterfølgende til overudglatning af kanter, hvilket resulterer i slørede billedkanter. TV-metoder med iterativ genvægtning er blevet implementeret for at reducere indflydelsen fra store gradientværdier i billederne. Dette er blevet anvendt i computertomografi (CT)-rekonstruktion som en metode, der er kendt som kantbevarende total variation. Da gradientstørrelserne anvendes til at estimere de relative straffevægte mellem datatroværdigheden og reguleringstermerne, er denne metode imidlertid ikke robust over for støj og artefakter og præcis nok til rekonstruktion af CS-billeder/signaler, og derfor kan den ikke bevare mindre strukturer.
Nylige fremskridt med hensyn til dette problem indebærer anvendelse af en iterativ retningsbestemt TV-forfining til CS-rekonstruktion. Denne metode består af to faser: i den første fase estimeres og forfines det oprindelige orienteringsfelt – som er defineret som et støjende punktvis indledende estimat af det givne billede ved hjælp af kantdetektion. I anden fase præsenteres CS-rekonstruktionsmodellen ved hjælp af en retningsbestemt TV-regularizer. Nedenfor gives flere oplysninger om disse TV-baserede tilgange – iterativt genvægtet l1-minimering, kantbevarende TV og iterativ model ved hjælp af retningsbestemt orienteringsfelt og TV-.
Eksisterende tilgange
Iterativt genvægtet l 1 {\displaystyle l_{1}}


minimering

I CS-rekonstruktionsmodellerne ved hjælp af begrænsede l 1 {\displaystyle l_{1}}

minimering, bliver større koefficienter straffet kraftigt i l 1 {\displaystyle l_{1}}}

norm. Det blev foreslået at have en vægtet formulering af l 1 {\displaystyle l_{1}}}

minimering designet til mere demokratisk at straffe ikke-nul-koefficienter. Der anvendes en iterativ algoritme til at konstruere de passende vægte. Hver iteration kræver løsning af en l 1 {\displaystyle l_{1}}}

minimeringsproblem ved at finde det lokale minimum af en konkav straffunktion, der mere ligner l 0 {\displaystyle l_{0}}

norm. En yderligere parameter, der normalt skal undgå skarpe overgange i straffunktionskurven, indføres i den iterative ligning for at sikre stabilitet, og således at et nulskøn i én iteration ikke nødvendigvis fører til et nulskøn i den næste iteration. Metoden går i det væsentlige ud på at bruge den aktuelle løsning til at beregne de vægte, der skal anvendes i den næste iteration.
For- og ulemper
I de tidlige iterationer kan man finde upræcise stikprøveestimater, men denne metode vil dog nedjustere disse på et senere tidspunkt for at give større vægt til de mindre ikke-nul-signalestimater. En af ulemperne er behovet for at definere et gyldigt startpunkt, da et globalt minimum måske ikke opnås hver gang på grund af funktionens konkavitet. En anden ulempe er, at denne metode har en tendens til at straffe billedgradienten ensartet, uanset de underliggende billedstrukturer. Dette medfører en overudglatning af kanter, især i områder med lav kontrast, hvilket efterfølgende fører til tab af information om lav kontrast. Fordelene ved denne metode er bl.a.: reduktion af samplingfrekvensen for sparsomme signaler; rekonstruktion af billedet, samtidig med at det er robust over for fjernelse af støj og andre artefakter; og brug af meget få iterationer. Dette kan også hjælpe med at genoprette billeder med sparsomme gradienter.
I figuren nedenfor henviser P1 til første trin i den iterative rekonstruktionsproces af projektionsmatrixen P for fan-beam-geometrien, som er begrænset af datatroværdighedstermen. Dette kan indeholde støj og artefakter, da der ikke foretages nogen regularisering. Minimeringen af P1 løses ved hjælp af metoden med konjugerede gradienter for mindste kvadrater. P2 henviser til det andet trin i den iterative rekonstruktionsproces, hvor der anvendes det kantbevarende reguleringsterm for den samlede variation til at fjerne støj og artefakter og dermed forbedre kvaliteten af det rekonstruerede billede/signal. Minimeringen af P2 sker ved hjælp af en simpel gradientafstigningsmetode. Konvergensen bestemmes ved efter hver iteration at teste, om billedet er positivt, ved at kontrollere, om f k – 1 = 0 {\displaystyle f^{{k-1}=0}

for det tilfælde, hvor f k – 1 < 0 {\displaystyle f^{k-1}<0}

(Bemærk, at f {\displaystyle f}

henviser til de forskellige lineære dæmpningskoefficienter for røntgenstråling ved forskellige voxels i patientbilledet).
Kantbevarende total variation (TV) baseret compressed sensing

Dette er en iterativ CT-rekonstruktionsalgoritme med kantbevarende TV-regularisering til rekonstruktion af CT-billeder fra stærkt underaftastede data opnået ved lav dosis CT gennem lave strømniveauer (milliampere). For at reducere billeddosis er en af de anvendte metoder at reducere antallet af røntgenprojektioner, der opfanges af scannerdetektorerne. Denne utilstrækkelige mængde projektionsdata, som anvendes til at rekonstruere CT-billedet, kan imidlertid forårsage strejfende artefakter. Desuden ender brugen af disse utilstrækkelige projektioner i standard-tv-algoritmer med at gøre problemet underbestemt og dermed føre til uendeligt mange mulige løsninger. I denne metode tildeles en yderligere strafvægtet funktion til den oprindelige tv-norm. Dette gør det lettere at opdage skarpe afbrydelser i intensiteten i billederne og dermed tilpasse vægten til at lagre den genvundne kantinformation under rekonstruktionen af signalet/billedet. Parameteren σ {\displaystyle \sigma }

styrer omfanget af den udjævning, der anvendes på pixelerne ved kanterne for at skelne dem fra de pixel, der ikke er kantpixels. Værdien af σ {\displaystyle \sigma }

ændres adaptivt på grundlag af værdierne af histogrammet for gradientstørrelsen, således at en vis procentdel af pixelerne har gradientværdier, der er større end σ {\displaystyle \sigma }

. Det kantbevarende samlede variationsterm bliver således mere sparsomt, og dette fremskynder gennemførelsen. Der anvendes en totrins-iterationsproces, der er kendt som fremad-fremad-ryggende opdelingsalgoritme. Optimeringsproblemet opdeles i to delproblemer, som derefter løses med henholdsvis den konjugerede gradient mindste kvadratmetode og den simple gradientafstigningsmetode. Metoden stoppes, når den ønskede konvergens er opnået, eller hvis det maksimale antal iterationer er nået.
For- og ulemper
Nogle af ulemperne ved denne metode er fraværet af mindre strukturer i det rekonstruerede billede og forringelse af billedopløsningen. Denne kantbevarende TV-algoritme kræver dog færre iterationer end den konventionelle TV-algoritme. Ved at analysere de horisontale og vertikale intensitetsprofiler af de rekonstruerede billeder kan det ses, at der er skarpe spring ved kantpunkter og ubetydelige, mindre udsving ved punkter uden for kantpunkterne. Denne metode fører således til en lav relativ fejl og en højere korrelation sammenlignet med tv-metoden. Den undertrykker og fjerner også effektivt enhver form for billedstøj og billedartefakter som f.eks. striber.
Iterativ model ved hjælp af et retningsbestemt orienteringsfelt og retningsbestemt total variation
For at undgå overudglatning af kanter og teksturdetaljer og for at opnå et rekonstrueret CS-billede, der er nøjagtigt og robust over for støj og artefakter, anvendes denne metode. Først foretages et indledende skøn over det støjende punktvise orienteringsfelt for billedet I {\displaystyle I}

, d ^ {{\displaystyle {\hat {d}}}

, fås. Dette støjende orienteringsfelt defineres således, at det kan raffineres på et senere tidspunkt for at reducere støjpåvirkningerne i orienteringsfeltets estimering. Der indføres derefter et groft orienteringsfeltestimat baseret på strukturtensor, der formuleres som følger J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 12 J 22 ) {\displaystyle J_{\rho }(\nabla I_{\sigma })=G_{\rho }*(\nabla I_{\sigma }\otimes \nabla I_{{\sigma })={{\begin{pmatrix}J_{11}&J_{12}\\J_{12}&J_{22}\end{pmatrix}}}

. Her er J ρ {\displaystyle J_{{\rho }}

henviser til den strukturtenor, der er relateret til billedpixelpunktet (i,j) med standardafvigelse ρ {\displaystyle \rho }

. G {\displaystyle G}

refererer til den gaussiske kerne ( 0 , ρ 2 ) {\displaystyle (0,\rho ^{2})}

med standardafvigelse ρ {\displaystyle \rho }

. σ {\displaystyle \sigma }

henviser til den manuelt definerede parameter for billedet I {\displaystyle I}

, under hvilken kantdetektionen er ufølsom over for støj. ∇ I σ σ {\displaystyle \nabla I_{\sigma }}

refererer til gradienten i billedet I {\displaystyle I}

og ( ∇ I σ ⊗ ∇ I σ ) {\displaystyle (\nabla I_{{\sigma }\otimes \nabla I_{{{\sigma })}

henviser til det tensorprodukt, der opnås ved at bruge denne gradient.
Den opnåede strukturtensor konvolveres med en Gaussisk kerne G {\displaystyle G}

for at forbedre nøjagtigheden af orienteringsestimatet med σ {\displaystyle \sigma }

sættes til høje værdier for at tage højde for de ukendte støjniveauer. For hver pixel (i,j) i billedet er strukturtenoren J en symmetrisk og positiv semidefinit matrix. Ved at konvolvere alle pixelerne i billedet med G {\displaystyle G}

, giver ortonormale egenvektorer ω og υ af J {\displaystyle J}

-matrixen. ω peger i retning af den dominerende orientering, der har den største kontrast, og υ peger i retning af den strukturorientering, der har den mindste kontrast. Orienteringsfeltets grove indledende estimation d ^ {\displaystyle {\hat {d}}}

er defineret som d ^ {\displaystyle {\hat {d}}}

= υ. Dette skøn er nøjagtigt ved stærke kanter. Ved svage kanter eller på områder med støj falder dens pålidelighed imidlertid.
For at overvinde denne ulempe defineres en forfinet orienteringsmodel, hvor datatermen reducerer effekten af støj og forbedrer nøjagtigheden, mens den anden strafterm med L2-normen er en troværdighedsterm, der sikrer nøjagtigheden af den indledende grove estimation.
Dette orienteringsfelt indføres i den retningsbestemte samlede variationsoptimeringsmodel til CS-rekonstruktion ved hjælp af ligningen: m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}

. X {\displaystyle \mathrm {X} }

er det objektive signal, som skal genfindes. Y er den tilsvarende målevektor, d er det iterative raffinerede orienteringsfelt, og Φ {\displaystyle \Phi }

er CS-målematrixen. Denne metode gennemgår nogle få gentagelser, der i sidste ende fører til konvergens. d ^ { {\displaystyle {\hat {d}}}

er orienteringsfeltets tilnærmede estimering af det rekonstruerede billede X k – 1 {\displaystyle X^{k-1}}}

fra den foregående iteration (for at kontrollere konvergensen og den efterfølgende optiske ydeevne anvendes den foregående iteration). For de to vektorfelter, der er repræsenteret ved X {\displaystyle \mathrm {X} }

og d {\displaystyle d}

, X ∙ d {\displaystyle \mathrm {X} \bullet d}

henviser til multiplikationen af de respektive horisontale og vertikale vektorelementer af X {\displaystyle \mathrm {X} }

og d {\displaystyle d}

efterfulgt af deres efterfølgende addition. Disse ligninger reduceres til en række konvekse minimeringsproblemer, som derefter løses med en kombination af variabelopdeling og augmented Lagrangian-metoder (FFT-baseret hurtig løser med en løsning i lukket form). Den (Augmented Lagrangian) anses for at svare til den opdelte Bregman-iteration, som sikrer konvergensen af denne metode. Orienteringsfeltet d er defineret som værende lig med ( d h , d v ) {\displaystyle (d_{h},d_{v})}

, hvor d h , d v {\displaystyle d_{h},d_{v}}

definerer de horisontale og vertikale estimater af d {\displaystyle d}

.

Den Augmented Lagrangian-metode for orienteringsfeltet, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}

, indebærer initialisering af d h , d v , H , V {\displaystyle d_{h},d_{v},H,V}

og derefter at finde den tilnærmede minimizer af L 1 {\displaystyle L_{1}}}

med hensyn til disse variabler. De lagrangiske multiplikatorer opdateres derefter, og den iterative proces stoppes, når konvergens er opnået. For den iterative retningsbestemte totalvariationsforfiningsmodel indebærer den forstærkede lagrangian-metode initialisering af X , P , Q , λ P , λ Q {\displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}

.
Her, H , V , P , Q {\displaystyle H,V,P,Q}

er nyligt indførte variabler, hvor H {\displaystyle H}

= ∇ d h {\displaystyle \nabla d_{h}}

, V {\displaystyle V}

= ∇ d v {\displaystyle \nabla d_{v}}

, P {\displaystyle P}

= ∇ X {\displaystyle \nabla \mathrm {X} }

, og Q {\displaystyle Q}

= P ∙ d {\displaystyle P\bullet d}

. λ H , λ V , λ P , λ Q {\displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}

er Lagrangian multiplikatorer for H , V , P , Q {\displaystyle H,V,P,Q}

. For hver iteration er den tilnærmede minimizer for L 2 {\displaystyle L_{2}}

med hensyn til variablerne ( X , P , Q {\displaystyle \mathrm {X} ,P,Q}

) beregnes. Og som i feltforfiningsmodellen opdateres de lagrangiske multiplikatorer, og den iterative proces stoppes, når der er opnået konvergens.
For orienteringsfeltforfiningsmodellen opdateres de lagrangske multiplikatorer i den iterative proces på følgende måde:
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) {\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {\displaystyle (\lambda _{V}})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k}})}

For den iterative retningsbestemte totale variationsforfiningsmodel opdateres Lagrangian-multiplikatorerne på følgende måde:
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}(P^{k}-\nabla (\mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) {\displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}\bullet d)}

Her, γ H , γ V , γ P , γ Q {\displaystyle \gamma _{H},\gamma _{V},\gamma _{V},\gamma _{P},\gamma _{Q}}

er positive konstanter.
Fordele og ulemper
Baseret på peak signal-til-støj-forholdet (PSNR) og strukturel lighedsindeks (SSIM) og kendte ground-truth-billeder til test af ydeevne konkluderes det, at iterativ retningsbestemt total variation har en bedre rekonstrueret ydeevne end de ikke-iterative metoder med hensyn til bevarelse af kant- og teksturområder. Orienteringsfeltforfiningsmodellen spiller en vigtig rolle i denne forbedring af ydeevnen, da den øger antallet af retningsløse pixels i det flade område, samtidig med at den forbedrer orienteringsfeltets konsistens i områder med kanter.