En forvirringsmatrix er en tabel, der ofte bruges til at beskrive en klassifikationsmodels (eller “klassifikators”) ydeevne på et sæt testdata, for hvilke de sande værdier er kendt. Selve forvirringsmatrixen er relativt enkel at forstå, men den relaterede terminologi kan være forvirrende.
Jeg ønskede at oprette en “quick reference guide” for terminologi for forvirringsmatrixer, fordi jeg ikke kunne finde en eksisterende ressource, der opfyldte mine krav: kompakt i præsentationen, med tal i stedet for vilkårlige variabler, og forklaret både i formler og sætninger.
Lad os starte med et eksempel på en forvirringsmatrix for en binær klassifikator (den kan dog let udvides til at omfatte mere end to klasser):
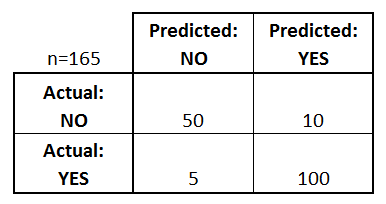
Hvad kan vi lære af denne matrix?
- Der er to mulige forudsagte klasser: “ja” og “nej”. Hvis vi f.eks. forudsagde tilstedeværelsen af en sygdom, ville “ja” betyde, at de har sygdommen, og “nej” ville betyde, at de ikke har sygdommen.
- Klassifikatoren lavede i alt 165 forudsigelser (f.eks, 165 patienter blev testet for tilstedeværelsen af den pågældende sygdom).
- Ud af disse 165 tilfælde forudsagde klassifikatoren “ja” 110 gange og “nej” 55 gange.
- I virkeligheden har 105 patienter i prøven sygdommen, og 60 patienter har den ikke.
Lad os nu definere de mest grundlæggende begreber, som er hele tal (ikke satser):
- true positives (TP): Det er tilfælde, hvor vi forudsagde ja (de har sygdommen), og de har faktisk sygdommen.
- true negatives (TN): Vi forudsagde nej, og de har ikke sygdommen.
- falsk positive (FP): Disse tilfælde er tilfælde, hvor vi forudsagde nej, og de har ikke sygdommen.
- falsk positive (FP): Vi forudsagde ja, men de har faktisk ikke sygdommen. (Også kendt som en “type I-fejl”.)
- falsk negative (FN): Vi forudsagde nej, men de har faktisk sygdommen. (Også kendt som en “Type II-fejl.”)
Jeg har tilføjet disse udtryk til forvirringsmatrixen og også tilføjet række- og kolonnetotalerne:
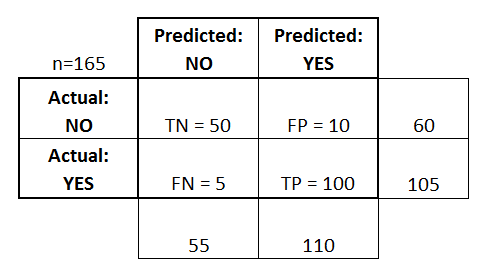
Dette er en liste over satser, der ofte beregnes ud fra en forvirringsmatrix for en binær klassifikator:
- Nøjagtighed:
- (TP+TN)/total = (100+50)/165 = 0,91
- Fejlklassifikationsrate:
- (FP+FN)/total = (10+5)/165 = 0,09
- ækvivalent med 1 minus nøjagtighed
- også kendt som “fejlprocent”
- Sandt positive procentdel: Når det faktisk er ja, hvor ofte forudsiger den så ja?
- TP/det faktiske ja = 100/105 = 0,95
- også kendt som “følsomhed” eller “tilbagekaldelse”
- Falsk positiv rate: Når det faktisk er nej, hvor ofte forudsiger den så ja?
- FP/det faktiske nej = 10/60 = 0,17
- True Negative Rate: Når det faktisk er nej, hvor ofte forudsiger den så nej?
- TN/aktuelt nej = 50/60 = 0,83
- ækvivalent med 1 minus False Positive Rate
- også kendt som “Specificitet”
- Præcision: Når det faktisk er nej, hvor ofte forudsiger den så nej?
- TP/forudset ja = 100/110 = 0,91
- aktuelt ja/total = 105/165 = 0,64
Et par andre udtryk er også værd at nævne:
- Nulfejlsrate: Dette er, hvor ofte du ville tage fejl, hvis du altid forudsagde majoritetsklassen. (I vores eksempel ville nulfejlprocenten være 60/165=0,36, fordi hvis du altid forudsagde ja, ville du kun tage fejl i de 60 “nej”-tilfælde). Dette kan være en nyttig basismåling til at sammenligne din klassifikator med. Den bedste klassifikator til en bestemt anvendelse vil dog undertiden have en højere fejlprocent end nulfejlprocenten, hvilket fremgår af nøjagtighedsparadokset.
- Cohen’s Kappa: Dette er i det væsentlige et mål for, hvor godt klassifikatoren klarede sig sammenlignet med, hvor godt den ville have klaret sig ved en tilfældighed. Med andre ord vil en model have en høj Kappa-score, hvis der er en stor forskel mellem nøjagtigheden og nulfejlprocenten. (Flere oplysninger om Cohen’s Kappa.)
- F Score: Dette er et vægtet gennemsnit af den sande positive rate (recall) og præcision. (Flere oplysninger om F-score.)
- ROC-kurve: Dette er en almindeligt anvendt graf, der opsummerer en klassifikators ydeevne over alle mulige tærskler. Den genereres ved at plotte den sande positive rate (y-aksen) mod den falske positive rate (x-aksen), efterhånden som du varierer tærsklen for tildeling af observationer til en given klasse. (Flere oplysninger om ROC-kurver.)
Og endelig, for dem af jer fra den bayesianske statistiks verden, er her et hurtigt resumé af disse termer fra Applied Predictive Modeling:
I forhold til bayesiansk statistik er sensitivitet og specificitet de betingede sandsynligheder, prævalensen er prioriteten, og de positive/negative forudsagte værdier er de posteriore sandsynligheder.
Vil du lære mere?
I min nye 35-minutters video, Making sense of the confusion matrix, forklarer jeg disse begreber mere indgående og dækker mere avancerede emner:
- Sådan beregner du præcision og tilbagekaldelse for problemer med flere klasser
- Sådan analyserer du en 10-klasses forvirringsmatrix
- Sådan vælger du den rigtige evalueringsmetrik til dit problem
- Hvorfor nøjagtighed ofte er en misvisende metrik
Lad mig vide, hvis du har spørgsmål!