Læringsmål
1. Konverter fra en enhed til en anden enhed af samme type.
I afsnit 2.2 “Udtryk af enheder” viste vi nogle eksempler på, hvordan man kan erstatte oprindelige enheder med andre enheder af samme type for at få en numerisk værdi, der er lettere at forstå. I dette afsnit vil vi formalisere processen.
Tænk på et simpelt eksempel: Hvor mange fod er der i 4 yards? De fleste mennesker vil næsten automatisk svare, at der er 12 fod i 4 yards. Hvordan har du foretaget denne bestemmelse? Tja, hvis der er 3 fod i 1 yard, og der er 4 yards, så er der 4 × 3 = 12 fod i 4 yards.
Det er naturligvis korrekt, men det er uformelt. Lad os formalisere det på en måde, der kan anvendes mere generelt. Vi ved, at 1 yard (yd) er lig med 3 fod (ft):
1 yd = 3 ft
I matematik kaldes dette udtryk for en lighed. Algebraens regler siger, at man kan ændre (dvs. gange eller dividere eller lægge til eller trække fra) ligheden (så længe man ikke dividerer med nul), og det nye udtryk vil stadig være en lighed. Hvis vi f.eks. dividerer begge sider med 2, får vi
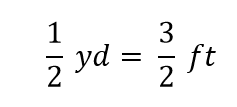
Vi kan se, at en halv yard er lig med 3/2, eller halvanden fod – noget, vi også ved er sandt, så ovenstående ligning er stadig en lighed. Hvis vi vender tilbage til den oprindelige lighed og antager, at vi dividerer begge sider af ligningen med 1 yard (antal og enhed):
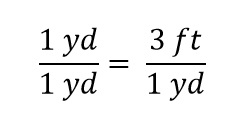
Udtrykket er stadig en lighed, efter algebraens regler. Den venstre brøk er lig med 1. Den har den samme mængde i tæller og nævner, så den må være lig med 1. Mængderne i tæller og nævner ophæver hinanden, både antallet og enheden:
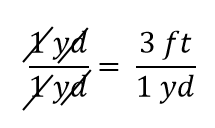
Når alt ophæves i en brøk, reduceres brøken til 1:
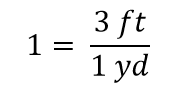
Vi har et udtryk, 3 ft1 yd, der er lig med 1. Det er en mærkelig måde at skrive 1 på, men det giver mening: 3 ft er lig med 1 yd, så mængderne i tælleren og nævneren er den samme størrelse, blot udtrykt med forskellige enheder. Udtrykket 3 ft1 yd kaldes en omregningsfaktor, og det bruges til formelt at ændre en størrelses enhed til en anden enhed. (Processen med at omregne enheder på en sådan formel måde kaldes nogle gange dimensionsanalyse eller faktormærkningsmetoden.)
For at se, hvordan dette sker, skal vi starte med den oprindelige mængde:
4 yd
Lad os nu gange denne mængde med 1. Når man ganger noget med 1, ændrer man ikke værdien af mængden. I stedet for at gange med bare 1, så lad os skrive 1 som 3 ft1 yd:
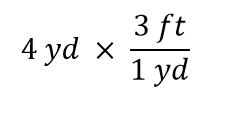
Det 4 yd udtryk kan opfattes som 4 yd/1; det vil sige, at det kan opfattes som en brøk med 1 i nævneren. Vi er i det væsentlige ved at multiplicere brøker. Hvis den samme ting optræder i tælleren og nævneren i en brøk, ophæves de. I dette tilfælde er det, der annulleres, enheden yard:
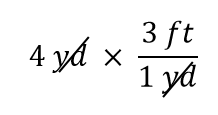
Det er alt, hvad vi kan annullere. Nu skal du gange og dividere alle tallene for at få det endelige svar: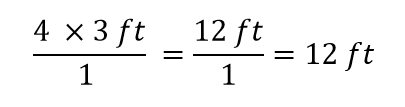
Vi får igen et svar på 12 ft, ligesom vi gjorde oprindeligt. Men i dette tilfælde har vi brugt en mere formel fremgangsmåde, som kan anvendes til en lang række problemer.
Hvor mange millimeter er der i 14,66 m? For at besvare dette spørgsmål skal vi konstruere en omregningsfaktor mellem millimeter og meter og anvende den korrekt på den oprindelige mængde. Vi starter med definitionen af en millimeter, som er
1 mm = 1/1.000 m
Den 1/1.000 er det, som præfikset milli- betyder. De fleste mennesker er mere trygge ved at arbejde uden brøker, så vi omskriver denne ligning ved at bringe de 1.000 ind i tælleren på den anden side af ligningen:
1.000 mm = 1 m
Nu konstruerer vi en omregningsfaktor ved at dividere den ene mængde i begge sider. Men nu opstår der et spørgsmål: Hvilken mængde skal vi dividere med? Det viser sig, at vi har to valgmuligheder, og de to valgmuligheder vil give os forskellige omregningsfaktorer, som begge er lig med 1:
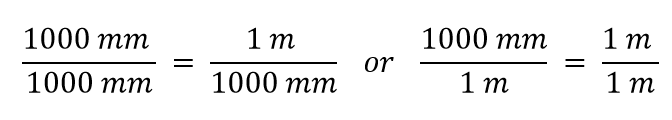
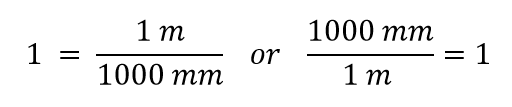
Hvilken omregningsfaktor skal vi bruge? Svaret er baseret på, hvilken enhed du ønsker at slippe af med i din oprindelige mængde. Den oprindelige enhed i vores mængde er meter, som vi ønsker at konvertere til millimeter. Fordi den oprindelige enhed antages at være i tælleren, skal vi for at slippe af med den have meterenheden i nævneren; så vil de ophæve hinanden. Derfor vil vi bruge den anden omregningsfaktor. Ved at annullere enhederne og udføre matematikken får vi
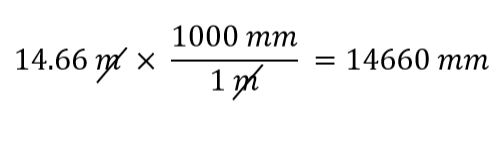
Bemærk, hvordan m annulleres, hvilket efterlader mm, som er den pågældende enhed.
Evnen til at konstruere og anvende korrekte omregningsfaktorer er en meget kraftfuld matematisk teknik i kemi. Du er nødt til at beherske denne teknik, hvis du skal have succes i dette og fremtidige kurser.
Eksempel 7
- Omregn 35,9 kL til liter.
- Omregn 555 nm til meter.
Løsning
-
Vi vil bruge det faktum, at 1 kL = 1.000 L. Af de to omregningsfaktorer, der kan defineres, er den, der vil virke, 1.000 L/1 kL. Ved at anvende denne omregningsfaktor får vi
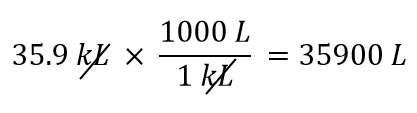
-
Vi vil bruge det faktum, at 1 nm = 1/1.000.000.000.000 m, hvilket vi omskriver som 1.000.000.000 nm = 1 m, eller 109 nm = 1 m. Af de to mulige omregningsfaktorer har den passende enheden nm i nævneren: 1 m/109 nm. Ved at anvende denne omregningsfaktor får vi
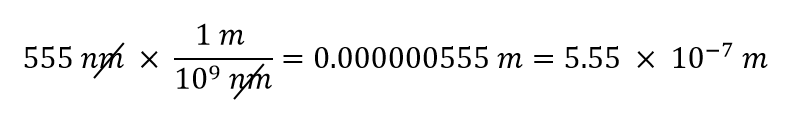
I det sidste trin udtrykte vi svaret i videnskabelig notation.
Test Yourself
- Konverter 67.08 μL til liter.
- Omregn 56,8 m til kilometer.
Svar
- 6,708 × 10-5 L
- 5,68 × 10-2 km
Hvad sker der, hvis vi har en afledt enhed, der er et produkt af mere end én enhed, f.eks. m2? Antag, at vi ønsker at konvertere kvadratmeter til kvadratcentimeter? Nøglen er at huske, at m2 betyder m × m, hvilket betyder, at vi har to meter-enheder i vores afledte enhed. Det betyder, at vi er nødt til at medtage to omregningsfaktorer, en for hver enhed. For eksempel for at konvertere 17,6 m2 til kvadratcentimeter udfører vi konverteringen på følgende måde:
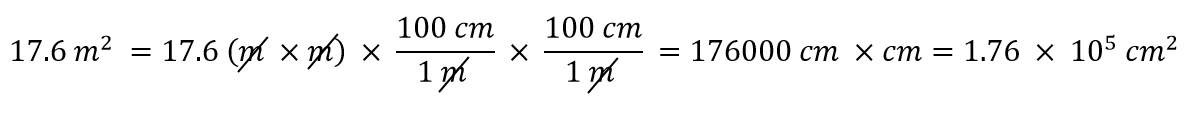
Eksempel 8
Hvor mange kubikcentimeter er der i 0.883 m3?
Løsning
Med en eksponent på 3 har vi tre længdeenheder, så i forlængelse heraf er vi nødt til at bruge tre omregningsfaktorer mellem meter og centimeter. Vi har således
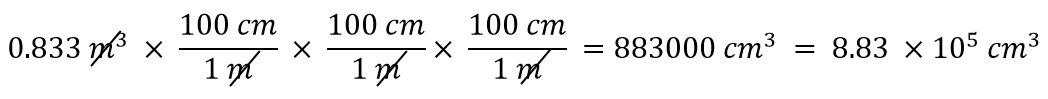
Du skal demonstrere for dig selv, at de tre meterenheder faktisk ophæver hinanden.
Test dig selv
Hvor mange kubikmillimeter er der i 0,0923 m3?
Svar
9,23 × 107 mm3
Sæt, at den enhed, du vil omregne, står i nævneren i en afledt enhed; hvad er det så? I omregningsfaktoren skal den enhed, du ønsker at fjerne, så være i tælleren. Dette vil ophæve den oprindelige enhed i nævneren og indføre en ny enhed i nævneren. Følgende eksempel illustrerer denne situation:
Eksempel 9
Konverter 88,4 m/min til meter/sekund.
Løsning
Vi ønsker at ændre enheden i nævneren fra minutter til sekunder. Da der er 60 sekunder i 1 minut (60 s = 1 min), konstruerer vi en omregningsfaktor, så den enhed, vi ønsker at fjerne, minutter, står i tælleren: 1 min/60 s. Anvend og udfør regnestykket:
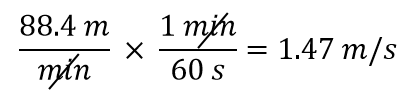
Bemærk, hvordan 88,4 automatisk kommer i tælleren. Det skyldes, at ethvert tal kan tænkes som værende i tælleren af en brøk divideret med 1.
Test dig selv
Konverter 0,203 m/min til meter/sekund.
Svar
0.00338 m/s eller 3,38 × 10-3 m/s
Figur 2.8 Hvor hurtigt er hurtigt?
Kilde: Kilde: