Kompressibilitetsfaktor (gasser) - Knowino

Fra Knowino

Dette er en kontrolleret version af denne side

Gå til: navigation,søgning

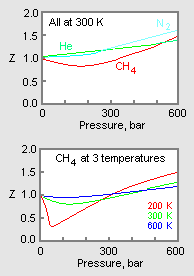
Figur 1: Eksempelgrafer for kompressibilitetsfaktorer for gasser

Kompressibilitetsfaktoren (Z) er en nyttig termodynamisk egenskab til at ændre idealgasloven for at tage højde for virkelige gassers adfærd. Den er et mål for, hvor meget de termodynamiske egenskaber for en virkelig gas afviger fra dem, der forventes for en idealgas. Den kan opfattes som forholdet mellem det faktiske volumen af en virkelig gas og det volumen, der forudsiges af den ideelle gas ved samme temperatur og tryk som det faktiske volumen.

For en idealgas har Z altid værdien 1. For virkelige gasser kan værdien afvige positivt eller negativt, afhængigt af virkningen af gassens intermolekylære kræfter. Jo tættere en virkelig gas er på sit kritiske punkt eller på sit mætningspunkt, jo større er gassens afvigelser fra den ideelle opførsel.

Den øverste graf i figur 1 illustrerer, hvordan kompressibilitetsfaktoren varierer for forskellige gasser ved samme temperatur og tryk. Den nederste graf illustrerer, hvordan kompressibilitetsfaktoren for en gas (f.eks. metan) ved et givet tryk varierer med temperaturen.

Denne artikel omhandler kun kompressibilitetsfaktoren for gasser og dykker ikke ned i kompressibiliteten for væsker eller damp-væske-blandinger.

Indhold

1 Bestemmelse af kompressibilitetsværdier for gasser
- 1.1 Generaliserede grafer for kompressibilitetsfaktorer for rene gasser
- 1.2 Generaliserede grafer for kompressibilitetsfaktorer for gasblandinger
- 1.3 Van der Waals-ligningen
  - 1.3.1 Modificerede versioner af van der Waals-ligningen
    - 1.3.1.1.1 Redlich-Kwong
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
- 1.4 Virial tilstandsligning
- 1.5 Andre tilstandsligninger
- 1.6 Notation for gaskonstanten
2 Referencer

Bestemmelse af værdier for gassens kompressibilitet

Den ideelle gaslov er defineret som:

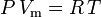
$P\,V_\mathrm{m} = R\,T$

og den ideelle gaslov korrigeret for ikke-idealitet er defineret som:

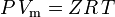
$P\,V_\mathrm{m} = ZR\,T$

hvor:
P	= tryk
	Vm	= molært volumen af gassen
Z	= kompressibilitetsfaktor
R	= universel gaskonstant
T	= temperatur

og således:

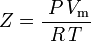
$Z = \frac{\;P\;P\,V_\\mathrm{m}}}{R\,T}$

som er den enkleste og mest udbredte tilstandsligning for reelle gasser (EOS). Den største begrænsning ved denne tilstandsligning er, at kompressibilitetsfaktoren, Z, ikke er en konstant, men varierer fra gas til gas samt med temperaturen og trykket for den pågældende gas. Den skal bestemmes eksperimentelt.

Hvis der foreligger eksperimentelle data for specifikke gasser, kan disse data anvendes til at fremstille grafer (som f.eks. i figur 1) af Z over tryk ved en konstant temperatur eller af Z over tryk ved forskellige temperaturer for disse specifikke gasser. Sådanne grafer er nyttige til let at opnå interpolerede værdier af Z mellem de eksperimentelt bestemte værdier.

Kompressibilitetsfaktoren kan som tidligere nævnt også udtrykkes som:

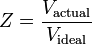
$Z = \frac{V_\mathrm{aktuel}}}{V_\mathrm{ideal}}}$

Der er tre regimer, der påvirker kompressibilitetsfaktoren:

værdien af Z tenderer mod 1, efterhånden som gastrykket nærmer sig 0, hvor alle gasser tenderer mod ideel adfærd
værdien af Z er mindre end 1 ved mellemliggende tryk, fordi de intermolekylære tiltrækningskræfter bevirker, at de faktiske volumener er mindre end de ideelle værdier
værdien af Z er større end 1 og tenderer i sidste ende mod uendeligt ved høje tryk, fordi de intermolekylære frastødende kræfter forårsager, at de faktiske volumener er større end idealværdierne

Generaliserede grafer over kompressibilitetsfaktoren for rene gasser

Den unikke sammenhæng mellem kompressibilitetsfaktoren og den reducerede temperatur, Tr, og det reducerede tryk, Pr, blev først erkendt af van der Waals i 1873 og er kendt som det såkaldte to-parameterprincip for tilsvarende tilstande. Princippet om tilsvarende tilstande udtrykker den generalisering, at de egenskaber ved en gas, som er afhængige af intermolekylære kræfter, er relateret til gassens kritiske egenskaber på en universel måde. Det giver et yderst vigtigt grundlag for udvikling af korrelationer mellem molekylære egenskaber.

Med hensyn til gassers kompressibilitet angiver princippet om tilsvarende tilstande, at enhver ren gas ved samme reducerede temperatur, Tr, og reducerede tryk, Pr, bør have den samme kompressibilitetsfaktor.

Den reducerede temperatur og det reducerede tryk er defineret som:

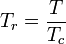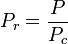
$T_r = \frac{T}{T_c}$ og $P_r = \frac{P}{P_c}$

Tc og Pc er kendt som den kritiske temperatur og det kritiske tryk for en gas. De er karakteristiske for hver specifik gas, hvor Tc er den temperatur, over hvilken det ikke er muligt at likvidere en given gas, og Pc er det mindste tryk, der kræves for at likvidere en given gas ved dens kritiske temperatur. Tilsammen definerer de det kritiske punkt for en væske, hvorover der ikke findes forskellige væske- og gasfaser i en given væske.

Tryk-volume-temperatur-data (PVT) for virkelige gasser varierer fra den ene rene gas til den anden. Men når kompressibilitetsfaktorerne for forskellige enkeltkomponentgasser grafisk vises over tryk sammen med temperaturisotermer (som vist for methan i den nederste graf i figur 1), viser mange af graferne lignende isotermeformer.

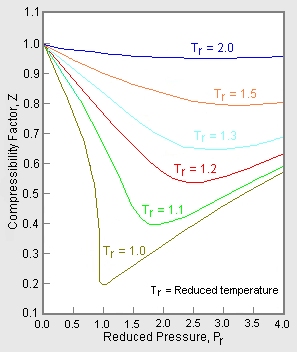
Figur 2: Eksempel på en generaliseret graf for kompressibilitetsfaktor

For at opnå en generaliseret graf, der kan anvendes for mange forskellige gasser, anvendes det reducerede tryk og den reducerede temperatur, Pr og Tr, til at normalisere kompressibilitetsfaktordataene. Figur 2 er et eksempel på en generaliseret kompressibilitetsfaktor-graf, der er afledt af hundredvis af eksperimentelle P-V-T-datapunkter for 10 rene gasser, nemlig methan, ethan, ethylen, propan, n-butan, i-pentan, n-hexan, nitrogen, kuldioxid og damp.

Der findes mere detaljerede generaliserede grafer over kompressibilitetsfaktorer baseret på op til 25 eller flere forskellige rene gasser, såsom Nelson-Obert-graferne. Sådanne grafer siges at have en nøjagtighed inden for 1-2 procent for Z-værdier større end 0,6 og inden for 4-6 procent for Z-værdier på 0,3-0,6.

De generaliserede kompressibilitetsfaktor-grafer kan være betydeligt fejlbehæftede for stærkt polære gasser, som er gasser, for hvilke centrene for positiv og negativ ladning ikke er sammenfaldende. I sådanne tilfælde kan skønnet for Z være fejlbehæftet med op til 15-20 procent.

Kvantegasserne hydrogen, helium og neon er ikke i overensstemmelse med den tilsvarende tilstandsadfærd, og det reducerede tryk og den reducerede temperatur for disse tre gasser bør omdefineres på følgende måde for at forbedre nøjagtigheden af forudsigelsen af deres kompressibilitetsfaktorer ved anvendelse af de generaliserede grafer:

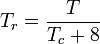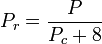
$T_r = \frac{T}{T_c + 8}$ og $P_r = \frac{P}{P_c + 8}$

hvor temperaturerne er i grader Kelvin og trykkene er i atmosfærer.

Generaliserede kompressibilitetsfaktordiagrammer for gasblandinger

De generaliserede kompressibilitetsfaktordiagrammer for rene gasser (som f.eks. eksemplificeret i figur 2 eller Nelson-Obert-diagrammerne kan også anvendes for gasblandinger ved hjælp af Kays regel, som W. B. Kay foreslog i 1936. Denne regel forudsiger en gasblandings P-V-T-adfærd ved at bestemme kompressibilitetsfaktoren for en gasblanding ved den reducerede temperatur og det reducerede tryk defineret ved den pseudokritiske temperatur, Tpc, og det pseudokritiske tryk, Ppc, der er defineret som:

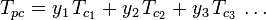
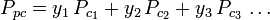
$T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_c_2} + y_3\,T_{c_c_3}\,\dots$ $P_{pc}} = y_1\,P_{c_1} + y_2\\,P_{c_c_2} + y_3\,P_{c_c_3}\,\dots$

hvor:
Tpc	= den pseudokritiske temperatur for gasblandingen
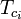$T_{c_i}$	= den kritiske temperatur for en komponent i gasblandingen
Ppc	= den pseudokritiske tryk i gasblandingen
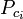$P_{c_i}$	= den kritiske temperatur for en af gasblandingens komponenter
yi	= mol- (eller volumen)brøkdelen af en af gasblandingens komponenter

den pseudoreducerede temperatur, Tpr, og det pseudoreducerede tryk, Ppr, til brug med de generaliserede kompressibilitetsfaktordiagrammer for rene gasser er derefter:

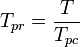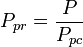
$T_{pr} = \frac{T}{T_{pc}}$ og $P_{pr} = \frac{P}{P_{pc}}$

En kompressibilitetsfaktordiagram for naturgas (som er en blanding af kulbrinte og andre gasser) med pseudoreducerede temperaturer og tryk er tilgængelig på internettet.

Van der Waals-ligningen

Van der Waals-ligningen blev udviklet i 1873 og kan udtrykkes som:

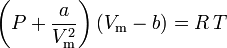
$\left(P + \frac{a}{V_\mathrm{m}^2}\right)\left(V_\mathrm{m} - b\right) = R\,T$

hvor:

a er et mål for styrken af tiltrækningen mellem gasmolekylerne b tager højde for det volumen, der er optaget af gasmolekyler, hvilket reducerer det tilgængelige åbne volumen

Van der Waals-ligningen kan omformuleres som:

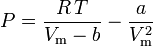
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

og komprimerbarhedsfaktoren kan skrives som:

Z = \frac{\;P\,V_\mathrm{m}}{R\,T} = \frac{V_\mathrm{m}}{R\,T}\left(\frac{R\,T}{V_\mathrm{m}} – b} – \frac{a}{V_\mathrm{m}^2}\right)

og vi har nu en ligning til bestemmelse af Z ved hjælp af van der Waals-parametrene a og b:

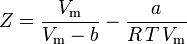
$Z = \frac{V_{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}}$

Og selv om a og b omtales som “Van der Waals-konstanterne”, er de ikke reelt konstanter, fordi de varierer fra den ene gas til den anden; de er dog uafhængige af P, V og T. Med andre ord er de konstante for den pågældende gas. Givet den kritiske temperatur og det kritiske tryk for en bestemt gas kan a og b fås for denne bestemte gas ud fra disse ligninger:

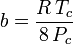
$a = \frac{27\, R^2\, T_c^2}{64\, P_c}$ og $b = \frac{R\, T_c}{8\, P_c}$

Til eksempel: Det kritiske tryk for ethan er 4.884 MPa, og den kritiske temperatur er 305,43 K (32,3˚C). Ved anvendelse af den universelle gaskonstant R på 8,3145 Pa m3 K-1 mol-1 giver ovenstående ligninger a = 0,557 m6 Pa mol-2 og b = 6,500×10-5 m3 mol-1.

Tabellerede værdier af a og b for forskellige gasser findes i disse referencer samt i mange andre kilder i den tekniske litteratur.

Modificerede versioner af van der Waals-ligningen

Bestemmelse af kompressibilitetsfaktorer ved hjælp af van der Waals-tilstandsligningen er en forbedring i forhold til anvendelse af de generaliserede kompressibilitetsdiagrammer. Der findes imidlertid modificerede versioner af van der Waals-tilstandsligningen, som giver en endnu større forbedring. De måske mest almindeligt anvendte tilstandsligninger af ingeniører, der arbejder inden for olieraffinering, petrokemisk produktion, naturgasbehandling, kryogen destillation og beslægtede industrier, er: Redlich-Kwong-ligningen, der blev udviklet i 1949, Soave-Redlich-Kwong-ligningen, der blev udviklet i 1972, og Peng-Robinson-ligningen, der blev udviklet i 1976. Disse tre ligninger er i det væsentlige modificerede versioner af van der Waals-ligningen. De sammenlignende ligninger er:

Redlich-Kwong

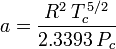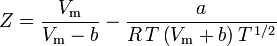
P = \frac{R\,T}{V_\mathrm{m} – b} – \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)T^{\,1/2}}} $a = \frac{R^2\, T_c^{\,5/2}}}{2.3393\, P_c}$ og $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{{\,1/2}}}$

Soave-Redlich-Kwong

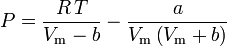
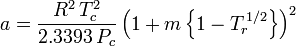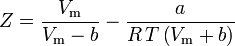
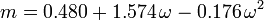
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)}$ $a = \frac{R^2\,T_c^2}{2.3393\,P_c}\, \Big(1 + m\, \Big\{1 - T_r^{\,1/2} \Big\} \Big\} \Big)^2$ og $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)}$ $m = 0.480 + 1.574\, \omega - 0.176\, \omega^2$

Den acentriske faktor, ω, der anvendes som en parameter i Soave-Redlich-Kwong- og Peng-Robinson-ligningerne blev først introduceret af Pitzer et al. i 1955. Den kan udtrykkes som:

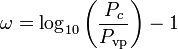
$\omega = \log_{10} \left(\frac{P_c}{P_\mathrm{vp}}}\right) - 1$

hvor Pvp er gassens mættede damptryk ved en temperatur på 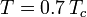$T = 0,7\, T_c$ .

Peng-Robinson

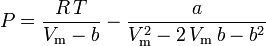
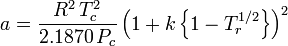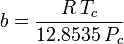
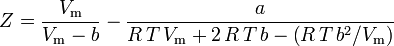
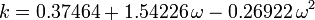
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}\, b - b^2}$ $a = \frac{R^2\,T_c^2}{2.1870\,P_c}\, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big\} \Big)^2$ og $b = \frac{R\, T_c}{12.8535\, P_c}$ $Z = \frac{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m} + 2\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)}$ $k = 0.37464 + 1.54226\, \omega - 0.26922\, \omega^2$

Virial tilstandsligning

Den mest fundamentale tilstandsligning , idet den har det mest solide teoretiske grundlag, er den viriale tilstandsligning:

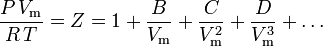
$\frac{P\,V_\mathrm{m}}{R\,T}} = Z = 1 + \frac{B}{V_\mathrm{m}} + \frac{C}{V_\mathrm{m}}^2} + \frac{D}{V_\mathrm{m}^3} + \dots$

Det blev først foreslået på et empirisk grundlag af Thiesen i 1885 og videreudviklet i 1901 af Kamerlingh-Onnes. Et statistisk-mekanisk udtryk for B blev først udledt af Ornstein i hans ph.d.-afhandling. Ligningen blev efterfølgende genudviklet af H.D. Ursell i 1927 på et teoretisk grundlag afledt af en statistisk-mekanisk (klynge)analyse af intermolekylære kræfter.

Parametrene B, C og D betegnes som henholdsvis den anden, tredje og fjerde virialkoefficient. Koefficienterne er ikke konstanter, da de varierer fra den ene gas til den anden såvel som temperaturen af den pågældende gas. De skrives undertiden som B(T), C(T) og D(T) for at angive, at de er funktioner af temperaturen. Koefficienternes numeriske værdi skal bestemmes eksperimentelt.

Den anden virialkoefficient udgør den største del af korrektionen for en gas’ ikke-ideelle opførsel. Derfor afkortes virialligningen undertiden efter den term, der indeholder den anden koefficient. Når den tredje koefficient er tilgængelig, afkortes ligningen imidlertid normalt efter den term, der indeholder den tredje koefficient. Den fjerde koefficient er sjældent tilgængelig.

En omfattende samling af virialkoefficienter for rene gasser og gasblandinger blev udarbejdet fra virialkoefficientdatabasen ved Thermodynamics Research Center, tidligere ved Texas A&M University, College Station, Texas, og nu placeret ved National Institute of Standards and Technology (NIST), Boulder, Colorado. Den seneste version af denne samling blev offentliggjort i 2003. NIST tilbyder også til køb et softwareprogram, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), der indeholder anden og tredje virialkoefficienter samt et væld af andre termodynamiske egenskaber.

Andre tilstandsligninger

Der findes en række andre tilstandsligninger til forudsigelse af virkelige gassers adfærd. De mest kendte er måske Beattie-Bridgeman-ligningen, der blev udviklet i 1929, og Benedict-Rubin-Webb-ligningen, der blev udviklet i 1940. Generelt er de mere komplekse end de ovenfor omtalte ligninger.

Notation for gaskonstanten

Gaskonstanten, der anvendes i denne artikel, er den universelle gaskonstant, R, der gælder for alle gasser. Der findes også en specifik gaskonstant, som kan betegnes som Rs, og som er defineret som Rs = R / M, hvor M er molekylvægten.

Der er desværre mange forfattere i den tekniske litteratur, der nogle gange bruger R som den specifikke gaskonstant uden at betegne den som sådan eller angive, at det er den specifikke gaskonstant. Dette kan og fører til forvirring.

1,0 1,1 1,1 1,2 1,3 1,4 McQuarrie, Donald A. og Simon, John D. (1999). Molekylær termodynamik. University Science Books. ISBN 1-891389-05-X.
2.0 2.1 2.1 2.2 2.2 2.3 2.4 Yunus A. Çengal og Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, 2. udgave. McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.1 3.2 3.3 3.3 3.4 Smith, J.M. et al. (2005). Introduktion til kemiteknisk termodynamik, syvende udgave. McGraw Hill. ISBN 0-07-31044545-0.
4.0 4.1 4.1 4.2 4.3 4.4 4.4 4.5 4.6 Y.V.C. Rao (1997). Chemical Engineering Thermodynamics. Universities Press (Indien). ISBN 81-7371-048-1.
5.0 5.1 Gaslove (Foredrag af professor M.J. Mombourquette ved Queens University, Canada)
Hong Wei Xiang (2005). Princippet om korresponderende stater og dets praksis: Termodynamiske, transport- og overfladeegenskaber for væsker. Elsevier. ISBN 0-444-52062-7.
IUPAC Goldbook
Gouq-Jen Su (1946). “Modificeret lov om korresponderende tilstande”. Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.
9.0 9.1 Equations of State (Professor Lyes Kadem, Concordia University, Canada)
10.0 10.1 Equations of State (Forelæsningsmateriale anvendt af professor Sanford Klein ved University of Wisconsin-Madison, USA)
Richard W. Miller (1996). Flow Measurement Engineering Handbook, 3. udgave. McGraw-Hill. ISBN 0-0-07-042366-0. (Se figur G-1 på side G.145)
Kai-Fui Vincent Wong (2000). Termodynamik for ingeniører, 1. udgave. CRC Press. ISBN 0-8493-0232-3. (Se figur A-2, side 278}
Nelson-Obert Generalized Compressibility Charts (Diagrammer tilgængelige på internettet, fra hjemmesiden for San Diego State University, U.S.A.)
W.B.Kay (1936). “Gasser og dampe ved høj temperatur og højt tryk – kulbrinteholdig massefylde”. Industrial Engineering & Chemistry 28:1014. ISSN 0096-4484.
Yunus A. Çengal og Michael A. Bowes (2005). Termodynamik: An Engineering Approach, 5. udgave. McGraw-Hill. ISBN 0-07-2884959.
Real Gases (Lecture material used by Professor R.M. Price at Christian Brothers University, U.S.A.)
Properties of Natural Gases (Professor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
Robert C. Weast (Editor) (1975). Handbook of Chemistry and Physics, 56th Edition. CRC Press. ISBN 0-87819-455-X.
19.0 19.1 19.2 Kapitel 3: Equations of State (side 6-8 af 65 pdf-sider) (Del af ph.d.-afhandling af Ji Lin Wang, 2002, Swinbourne University of Technology, Australien)
20.0 20.1 20.2 Jean Vidal (2003). Termodynamik: Anvendelse i kemiteknik og i olieindustrien. Editions Technip. ISBN 2-7108-0800-5.
Zakia Nasri og Housam Binous (2007). “Applications of the Soave-Redlich-Kwong Equation of State Using Mathematica”. Journal of Chemical Engineering of Japan 40 (6): 534-538. Hentet herfra.
K.S. Pitzer et al (1955). “The Volumetric and Thermodynamic Properties of Fluids”. Journal of the American Chemical Society 77: 3427-3440.
Francis S. Manning og Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
Acentric Factor Definition (Physical Property Sources Index, PPSI, of the Swiss Federal Institute of Technology Zurich)
Max F. Thiesen (1885). “Undersøgelser af tilstandsligningen”. Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901). “Ekspression af tilstandsligningen for gasser og væsker ved hjælp af serier”. Commun. Phys. Lab. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Application of the statistical mechanics of Gibbs on molecular-theoretical problems), Leiden
H. D. Ursell (1927). “The Evaluation of Gibbs’ Phase Integral for Imperfect Gases” (23): 685.
J.D. Dymond og R.C. Wilhoit (forfattere), K.N. Marsch og M. Fenkel (redaktører) (2003). Virialkoefficienter for rene gasser og blandinger, 1. udgave. Springer. ISBN 3-540-4434040-1.
NIST Standard Reference Database 23
J.A. Beattie og O.C. Bridgeman (1929). “A New Equation of State for Fluids”. Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb og L.C. Rubin (1940). “An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures”. J. Chem. Phys. 8: 334-335.

Noget af indholdet på denne side kan tidligere have været vist på Citizendium.

Hentet fra “http://knowino.org/wiki/Compressibility_factor_(gases)”

Kategori: Fysik