Baryzentrische Koordinaten

Baryzentrische Koordinaten sind Dreiergruppen von Zahlen , die Massen entsprechen, die an den Eckpunkten eines Bezugsdreiecks liegen. Diese Massen bestimmen dann einen Punkt , der der geometrische Schwerpunkt der drei Massen ist und mit den Koordinaten identifiziert wird. Die Eckpunkte des Dreiecks sind durch , und gegeben. Baryzentrische Koordinaten wurden 1827 von Möbius entdeckt (Coxeter 1969, S. 217; Fauvel et al. 1993).

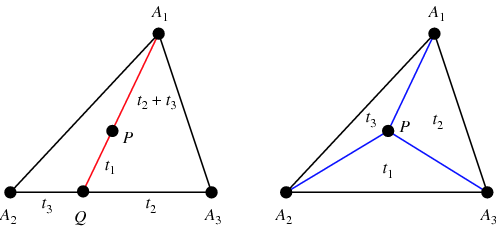
Um die baryzentrischen Koordinaten für einen beliebigen Punkt zu finden, bestimmt man und vom Punkt im Schnittpunkt der Geraden mit der Seite , und bestimme dann als die Masse bei , die eine Masse bei ausgleicht, wodurch zum Schwerpunkt wird (linke Abbildung). Außerdem sind die Flächen der Dreiecke , und proportional zu den baryzentrischen Koordinaten , und von (rechte Abbildung; Coxeter 1969, p. 217).

Baryzentrische Koordinaten sind homogen, also

(1)

für .

Baryzentrische Koordinaten, die so normiert sind, dass sie den tatsächlichen Flächen der Unterdreiecke entsprechen, nennt man homogene baryzentrische Koordinaten. Baryzentrische Koordinaten, die so normiert sind, dass

(2)

so dass die Koordinaten die Flächen der Unterdreiecke normiert mit der Fläche des ursprünglichen Dreiecks ergeben, werden Flächenkoordinaten genannt (Coxeter 1969, S. 218). Baryzentrische und Flächenkoordinaten können besonders elegante Beweise für geometrische Theoreme wie den Satz von Routh, den Satz von Ceva und den Satz des Menelaos liefern (Coxeter 1969, S. 219-221).

(Nicht notwendigerweise homogene) baryzentrische Koordinaten für eine Reihe von üblichen Zentren sind in der folgenden Tabelle zusammengefasst. In der Tabelle sind , und die Seitenlängen des Dreiecks und ist sein Halbmesser.

Dreiecksmittelpunkt	Baryzentrische Koordinaten
Umkreismittelpunkt	(, , )
excenter
excenter
excenter
Gergonne Punkt Ge	(, , )
incenter
Nagel point Na
Orthozentrum	(, , )
symmedianer Punkt
Dreiecksschwerpunkt

In baryzentrischen Koordinaten hat eine Linie eine lineare homogene Gleichung. Insbesondere hat die Linie, die die Punkte und verbindet, die Gleichung

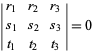(3)

(Loney 1962, pp. 39 und 57; Coxeter 1969, S. 219; Bottema 1982). Wenn die Eckpunkte eines Dreiecks baryzentrische Koordinaten haben, dann ist der Flächeninhalt des Dreiecks

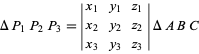(4)

(Bottema 1982, Yiu 2000).