Es handelt sich um stochastische Lernprozesse mit rekurrenter Struktur, die die Grundlage der frühen Optimierungstechniken in ANN bilden. Die Boltzmann-Maschine wurde 1985 von Geoffrey Hinton und Terry Sejnowski erfunden. Mehr Klarheit bieten die Worte von Hinton über die Boltzmann-Maschine.
„Eine überraschende Eigenschaft dieses Netzes ist, dass es nur lokal verfügbare Informationen verwendet. Die Änderung des Gewichts hängt nur vom Verhalten der beiden Einheiten ab, die es verbindet, obwohl die Änderung ein globales Maß optimiert“ – Ackley, Hinton 1985.
Einige wichtige Punkte über die Boltzmann-Maschine –
-
Sie verwenden eine rekurrente Struktur.
-
Sie bestehen aus stochastischen Neuronen, die einen der beiden möglichen Zustände haben, entweder 1 oder 0.
-
Einige der Neuronen in diesem Netzwerk sind adaptiv (freier Zustand) und einige sind geklammert (eingefrorener Zustand).
-
Wenn wir simuliertes Annealing auf das diskrete Hopfield-Netzwerk anwenden, dann wird es zur Boltzmann-Maschine.
Ziel der Boltzmann-Maschine
Der Hauptzweck der Boltzmann-Maschine ist die Optimierung der Lösung eines Problems. Die Aufgabe der Boltzmann-Maschine ist es, die Gewichte und Mengen in Bezug auf das jeweilige Problem zu optimieren.
Architektur
Das folgende Diagramm zeigt die Architektur der Boltzmann-Maschine. Aus dem Diagramm ist ersichtlich, dass es sich um eine zweidimensionale Anordnung von Einheiten handelt. Die Gewichte der Verbindungen zwischen den Einheiten sind hier -p, wobei p > 0 ist. Die Gewichte der Selbstverbindungen sind durch b gegeben, wobei b > 0 ist.
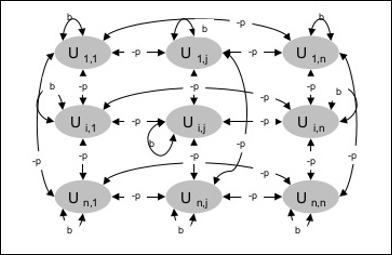
Trainingsalgorithmus
Da wir wissen, dass Boltzmann-Maschinen feste Gewichte haben, gibt es keinen Trainingsalgorithmus, da wir die Gewichte im Netzwerk nicht aktualisieren müssen. Um das Netzwerk zu testen, müssen wir jedoch die Gewichte setzen und die Konsensfunktion (CF) finden.
Die Boltzmann-Maschine hat einen Satz von Einheiten Ui und Uj und verfügt über bidirektionale Verbindungen.
-
Wir betrachten das feste Gewicht wij.
-
wij ≠ 0, wenn Ui und Uj verbunden sind.
-
Es gibt auch eine Symmetrie in der gewichteten Verbindung, d. h.d. h. wij = wji.
-
Es gibt auch eine Symmetrie in der gewichteten Verflechtung, d. h. es gäbe die Selbstverflechtung zwischen Einheiten.
-
Für jede Einheit Ui wäre ihr Zustand ui entweder 1 oder 0.
Das Hauptziel der Boltzmann-Maschine ist die Maximierung der Konsensfunktion (CF), die durch die folgende Beziehung gegeben werden kann
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
Wenn nun der Zustand entweder von 1 auf 0 oder von 0 auf 1 wechselt, dann kann die Änderung des Konsenses durch die folgende Beziehung gegeben werden –
$$$Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Hier ist ui der aktuelle Zustand von Ui.
Die Variation des Koeffizienten (1 – 2ui) ist durch die folgende Beziehung gegeben –
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:ist\:aktuell\:off\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
Im Allgemeinen ändert die Einheit Ui ihren Zustand nicht, aber wenn sie es tut, dann würde die Information lokal bei der Einheit verbleiben.
Die Wahrscheinlichkeit, dass das Netzwerk die Zustandsänderung der Einheit akzeptiert, ist durch die folgende Beziehung gegeben –
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Hier ist T der Kontrollparameter. Er nimmt ab, wenn CF den Maximalwert erreicht.
Testalgorithmus
Schritt 1 – Initialisieren Sie Folgendes, um mit dem Training zu beginnen –
- Gewichte, die die Randbedingungen des Problems darstellen
- Kontrollparameter T
Schritt 2 – Fahren Sie mit den Schritten 3-8 fort, wenn die Stoppbedingung nicht erfüllt ist.
Schritt 3 – Führen Sie die Schritte 4-7 durch.
Schritt 4 – Nehmen Sie an, dass einer der Zustände das Gewicht geändert hat und wählen Sie die ganze Zahl I, J als Zufallswerte zwischen 1 und n.
Schritt 5 – Berechnen Sie die Änderung des Konsenses wie folgt –
$$$$Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Schritt 6 – Berechnen Sie die Wahrscheinlichkeit, dass dieses Netzwerk die Zustandsänderung akzeptieren würde
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Schritt 7 – Akzeptiere oder lehne diese Änderung wie folgt ab –
Fall I – wenn R < AF, akzeptiere die Änderung.
Fall II – wenn R ≥ AF, lehne die Änderung ab.
Hier ist R eine Zufallszahl zwischen 0 und 1.
Schritt 8 – Reduziere den Kontrollparameter (Temperatur) wie folgt –
T(neu) = 0.95T(alt)
Schritt 9 – Prüfen Sie die Anhaltebedingungen, die wie folgt lauten können –
- Die Temperatur erreicht einen bestimmten Wert
- Es gibt keine Zustandsänderung für eine bestimmte Anzahl von Iterationen