Biographie

Brahmagupta (598-668 CE)
Der große indische Mathematiker und Astronom Brahmagupta aus dem 7. Jahrhundert schrieb einige wichtige Werke über Mathematik und Astronomie. Er stammte aus dem Bundesstaat Rajasthan im Nordwesten Indiens (er wird oft als Bhillamalacarya, der Lehrer aus Bhillamala, bezeichnet) und wurde später Leiter des astronomischen Observatoriums in Ujjain in Zentralindien. Die meisten seiner Werke sind in elliptischen Versen verfasst, wie sie in der indischen Mathematik zu jener Zeit üblich waren, und haben daher etwas Poetisches an sich.
Es scheint wahrscheinlich, dass Brahmaguptas Werke, insbesondere sein berühmtester Text, das „Brahmasphutasiddhanta“, vom abbasidischen Kalifen Al-Mansur im 8. Jahrhundert in sein neu gegründetes Bildungszentrum in Bagdad an den Ufern des Tigris gebracht wurden und so eine wichtige Verbindung zwischen der indischen Mathematik und Astronomie und dem aufkommenden Aufschwung von Wissenschaft und Mathematik in der islamischen Welt herstellten.
In seinem Werk über Arithmetik erklärte Brahmagupta, wie man den Würfel und die Kubikwurzel einer ganzen Zahl findet, und gab Regeln an, die die Berechnung von Quadraten und Quadratwurzeln erleichtern. Er gab auch Regeln für den Umgang mit fünf Arten von Kombinationen von Brüchen an. Er gab die Summe der Quadrate der ersten n natürlichen Zahlen als n(n + 1)(2n + 1)⁄ 6 und die Summe der Kuben der ersten n natürlichen Zahlen als (n(n + 1)⁄2)² an.
Brahmasphutasiddhanta – Die Null als Zahl behandeln

Brahmaguptas Regeln für den Umgang mit Null und negativen Zahlen
Brahmaguptas Genialität lag jedoch in seiner Behandlung des (damals relativ neuen) Konzepts der Zahl Null. Obwohl sie oft auch dem indischen Mathematiker Bhaskara I. aus dem 7. Jahrhundert zugeschrieben wird, ist sein „Brahmasphutasiddhanta“ wahrscheinlich der früheste bekannte Text, in dem die Null als eigenständige Zahl behandelt wird und nicht nur als Platzhalterziffer wie bei den Babyloniern oder als Symbol für eine fehlende Menge wie bei den Griechen und Römern.
Brahmagupta stellte die grundlegenden mathematischen Regeln für den Umgang mit der Null auf (1 + 0 = 1; 1 – 0 = 1; und 1 x 0 = 0), obwohl sein Verständnis der Division durch Null unvollständig war (er dachte, dass 1 ÷ 0 = 0 sei). Fast 500 Jahre später, im 12. Jahrhundert, zeigte ein anderer indischer Mathematiker, Bhaskara II, dass die Antwort Unendlichkeit und nicht Null sein sollte (mit der Begründung, dass 1 in eine unendliche Anzahl von Teilen der Größe Null geteilt werden kann), eine Antwort, die jahrhundertelang als richtig angesehen wurde. Diese Logik erklärt jedoch nicht, warum 2 ÷ 0, 7 ÷ 0 usw. ebenfalls Null sein sollte – die moderne Auffassung ist, dass eine durch Null geteilte Zahl eigentlich „undefiniert“ ist (d.h. sie ergibt keinen Sinn).
Brahmaguptas Auffassung von Zahlen als abstrakten Gebilden und nicht nur zum Zählen und Messen, ermöglichte ihm einen weiteren großen konzeptionellen Sprung, der tiefgreifende Folgen für die zukünftige Mathematik haben sollte. Bis dahin galt beispielsweise die Summe 3 – 4 entweder als bedeutungslos oder bestenfalls als Null. Brahmagupta erkannte jedoch, dass es so etwas wie eine negative Zahl geben konnte, die er als „Schuld“ im Gegensatz zu „Eigenschaft“ bezeichnete. Er erläuterte die Regeln für den Umgang mit negativen Zahlen (z. B. ist eine negative Zahl mal eine negative Zahl eine positive Zahl, eine negative Zahl mal eine positive Zahl eine negative Zahl usw.).
Außerdem wies er darauf hin, dass quadratische Gleichungen (z. B. vom Typ x2 + 2 = 11) theoretisch zwei mögliche Lösungen haben könnten, von denen eine negativ sein könnte, weil 32 = 9 und -32 = 9. Zusätzlich zu seinen Arbeiten über die Lösungen allgemeiner linearer Gleichungen und quadratischer Gleichungen ging Brahmagupta noch weiter, indem er Systeme simultaner Gleichungen (Gleichungssätze mit mehreren Variablen) betrachtete und quadratische Gleichungen mit zwei Unbekannten löste, etwas, das im Westen erst tausend Jahre später in Betracht gezogen wurde, als Fermat 1657 ähnliche Probleme betrachtete.
Brahmagupta’s Theorem über zyklische Vierecke
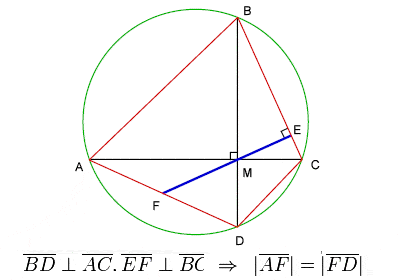
Brahmagupta’s Theorem über zyklische Vierecke
Brahmagupta versuchte sogar, diese eher abstrakten Konzepte niederzuschreiben, Er benutzte die Anfangsbuchstaben der Namen von Farben, um Unbekannte in seinen Gleichungen darzustellen, eine der frühesten Andeutungen dessen, was wir heute als Algebra kennen.
Brahmagupta widmete einen wesentlichen Teil seiner Arbeit der Geometrie und Trigonometrie. Er stellte √10 (3.162277) als einen guten praktischen Näherungswert für π (3.141593) auf und gab eine Formel, die heute als Brahmagupta-Formel bekannt ist, für den Flächeninhalt eines zyklischen Vierecks sowie ein berühmtes Theorem über die Diagonalen eines zyklischen Vierecks, das gewöhnlich als Brahmaguptas Theorem bezeichnet wird.
| << Zurück zu Indische Mathematik | Vorwärts zu Madhava >> |