Lernziel
1. Von einer Einheit in eine andere Einheit desselben Typs umrechnen.
In Abschnitt 2.2 „Einheiten ausdrücken“ haben wir einige Beispiele gezeigt, wie man anfängliche Einheiten durch andere Einheiten desselben Typs ersetzen kann, um einen Zahlenwert zu erhalten, der leichter zu verstehen ist. In diesem Abschnitt werden wir das Verfahren formalisieren.
Betrachten Sie ein einfaches Beispiel: Wie viele Fuß sind in 4 Yards? Die meisten Menschen werden fast automatisch antworten, dass es 12 Fuß in 4 Yards sind. Wie sind Sie zu diesem Ergebnis gekommen? Nun, wenn 1 Meter 3 Fuß sind und es 4 Meter gibt, dann sind es 4 × 3 = 12 Fuß in 4 Metern.
Das ist natürlich richtig, aber es ist informell. Lassen Sie es uns so formalisieren, dass es allgemeiner angewendet werden kann. Wir wissen, dass 1 Yard (yd) gleich 3 Fuß (ft) ist:
1 yd = 3 ft
In der Mathematik nennt man diesen Ausdruck eine Gleichheit. Die Regeln der Algebra besagen, dass man die Gleichheit ändern (d.h. multiplizieren oder dividieren oder addieren oder subtrahieren) kann (solange man nicht durch Null dividiert) und der neue Ausdruck immer noch eine Gleichheit ist. Wenn wir zum Beispiel beide Seiten durch 2 teilen, erhalten wir
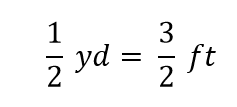
Wir sehen, dass ein halber Yard gleich 3/2 oder anderthalb Fuß ist – etwas, von dem wir auch wissen, dass es wahr ist, also ist die obige Gleichung immer noch eine Gleichheit. Um zur ursprünglichen Gleichheit zurückzukehren, nehmen wir an, wir teilen beide Seiten der Gleichung durch 1 yard (Zahl und Einheit):
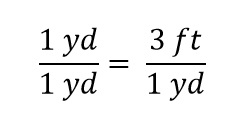
Der Ausdruck ist nach den Regeln der Algebra immer noch eine Gleichheit. Der linke Bruch ist gleich 1. Er hat die gleiche Menge im Zähler und im Nenner, also muss er gleich 1 sein. Die Mengen in Zähler und Nenner heben sich auf, sowohl die Zahl als auch die Einheit:
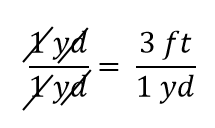
Wenn sich in einem Bruch alles aufhebt, reduziert sich der Bruch auf 1:
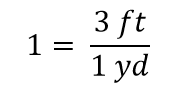
Wir haben einen Ausdruck, 3 ft1 yd, der gleich 1 ist. Das ist eine seltsame Art, 1 zu schreiben, aber es macht Sinn: 3 ft entsprechen 1 yd, also sind die Mengen im Zähler und im Nenner dieselbe Menge, nur mit unterschiedlichen Einheiten ausgedrückt. Der Ausdruck 3 ft1 yd wird als Umrechnungsfaktor bezeichnet und wird verwendet, um die Einheit einer Menge formal in eine andere Einheit zu ändern. (Der Prozess der Umrechnung von Einheiten auf eine solche formale Weise wird manchmal als Dimensionsanalyse oder Faktoretikettenmethode bezeichnet.)
Um zu sehen, wie dies geschieht, lassen Sie uns mit der ursprünglichen Menge beginnen:
4 yd
Nun lassen Sie uns diese Menge mit 1 multiplizieren. Wenn Sie etwas mit 1 multiplizieren, ändern Sie den Wert der Menge nicht. Anstatt nur mit 1 zu multiplizieren, schreiben wir 1 als 3 ft1 yd:
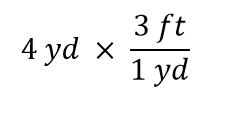
Den Term 4 yd kann man sich als 4 yd/1 vorstellen; das heißt, man kann ihn als Bruch mit 1 im Nenner betrachten. Wir multiplizieren im Wesentlichen Brüche. Wenn im Zähler und im Nenner eines Bruchs das Gleiche steht, heben sie sich auf. In diesem Fall hebt sich die Einheit Yard auf:
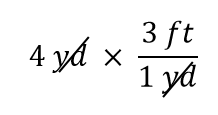
Das ist alles, was wir aufheben können. Multipliziere und teile nun alle Zahlen, um die endgültige Antwort zu erhalten: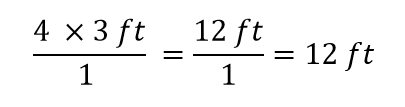
Auch hier erhalten wir eine Antwort von 12 ft, genau wie ursprünglich. Aber in diesem Fall haben wir ein formaleres Verfahren verwendet, das auf eine Vielzahl von Problemen anwendbar ist.
Wie viele Millimeter sind in 14,66 m? Um diese Frage zu beantworten, müssen wir einen Umrechnungsfaktor zwischen Millimetern und Metern konstruieren und ihn korrekt auf die ursprüngliche Größe anwenden. Wir beginnen mit der Definition eines Millimeters, die lautet:
1 mm = 1/1.000 m
Das 1/1.000 bedeutet die Vorsilbe Milli-. Die meisten Menschen arbeiten lieber ohne Brüche, also schreiben wir diese Gleichung um, indem wir die 1.000 in den Zähler der anderen Seite der Gleichung bringen:
1.000 mm = 1 m
Nun konstruieren wir einen Umrechnungsfaktor, indem wir eine Menge in beide Seiten teilen. Nun stellt sich aber die Frage, durch welche Größe wir dividieren sollen. Es stellt sich heraus, dass wir zwei Möglichkeiten haben, und die beiden Möglichkeiten geben uns unterschiedliche Umrechnungsfaktoren, die beide gleich 1 sind:
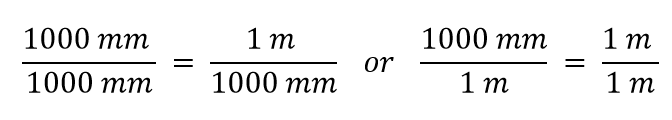
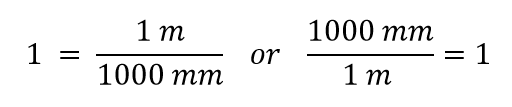
Welchen Umrechnungsfaktor verwenden wir? Die Antwort hängt davon ab, welche Einheit Sie in Ihrer Ausgangsmenge loswerden wollen. Die ursprüngliche Einheit unserer Menge ist Meter, die wir in Millimeter umrechnen wollen. Da die ursprüngliche Einheit im Zähler steht, muss die Einheit Meter im Nenner stehen, um sie loszuwerden; dann heben sie sich auf. Daher wird der zweite Umrechnungsfaktor verwendet. Wenn man die Einheiten aufhebt und die Mathematik durchführt, erhält man
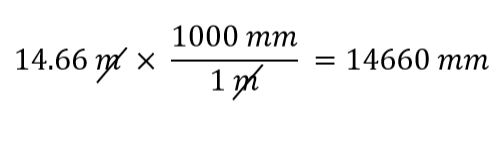
Beachten Sie, dass sich m aufhebt und mm übrig bleibt, die Einheit, die uns interessiert.
Die Fähigkeit, richtige Umrechnungsfaktoren zu konstruieren und anzuwenden, ist eine sehr mächtige mathematische Technik in der Chemie. Du musst diese Technik beherrschen, wenn du in diesem und zukünftigen Kursen erfolgreich sein willst.
Beispiel 7
- Umrechnung von 35,9 kL in Liter.
- Umrechnung von 555 nm in Meter.
Lösung
-
Wir verwenden die Tatsache, dass 1 kL = 1.000 L ist. Von den beiden Umrechnungsfaktoren, die definiert werden können, ist derjenige, der funktioniert, 1.000 L/1 kL. Bei Anwendung dieses Umrechnungsfaktors erhalten wir
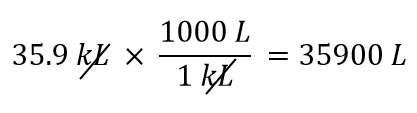
-
Wir werden die Tatsache verwenden, dass 1 nm = 1/1.000.000.000 m ist, was wir als 1.000.000.000 nm = 1 m oder 109 nm = 1 m umschreiben werden: 1 m/109 nm. Bei Anwendung dieses Umrechnungsfaktors erhalten wir
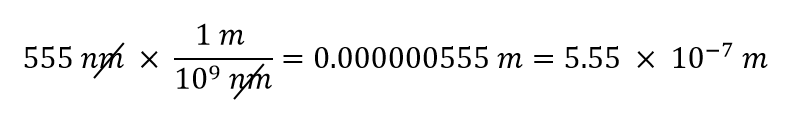
Im letzten Schritt haben wir die Antwort in wissenschaftlicher Notation ausgedrückt.
Teste dich selbst
- Umrechnen von 67.08 μL in Liter um.
- Umrechnen von 56,8 m in Kilometer.
Antworten
- 6,708 × 10-5 L
- 5,68 × 10-2 km
Was ist, wenn eine abgeleitete Einheit das Produkt aus mehreren Einheiten ist, wie z. B. m2? Angenommen, wir wollen Quadratmeter in Quadratzentimeter umrechnen. Der Schlüssel ist, sich daran zu erinnern, dass m2 m × m bedeutet, was bedeutet, dass wir zwei Metereinheiten in unserer abgeleiteten Einheit haben. Das bedeutet, dass wir zwei Umrechnungsfaktoren einbeziehen müssen, einen für jede Einheit. Um zum Beispiel 17,6 m2 in Quadratzentimeter umzurechnen, führen wir die Umrechnung wie folgt durch:
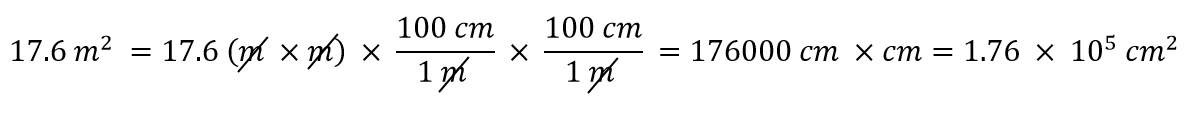
Beispiel 8
Wie viele Kubikzentimeter sind in 0.883 m3?
Lösung
Bei einem Exponenten von 3 haben wir drei Längeneinheiten, also müssen wir auch drei Umrechnungsfaktoren zwischen Metern und Zentimetern verwenden. Wir haben also
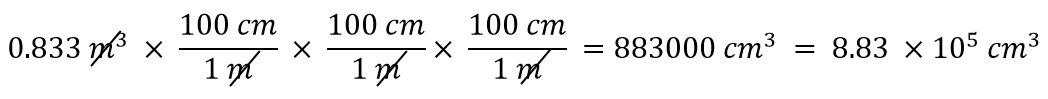
Du sollst dir selbst zeigen, dass sich die drei Metereinheiten tatsächlich aufheben.
Teste dich selbst
Wie viele Kubikmillimeter sind in 0,0923 m3 enthalten?
Antwort
9,23 × 107 mm3
Angenommen, die Einheit, die du umrechnen willst, steht im Nenner einer abgeleiteten Einheit; was dann? Dann muss im Umrechnungsfaktor die Einheit, die man entfernen möchte, im Zähler stehen. Dadurch wird die ursprüngliche Einheit im Nenner aufgehoben und eine neue Einheit im Nenner eingeführt. Das folgende Beispiel veranschaulicht diese Situation.
Beispiel 9
Umrechnung von 88,4 m/min in Meter/Sekunde.
Lösung
Wir wollen die Einheit im Nenner von Minuten in Sekunden ändern. Da 1 Minute 60 Sekunden hat (60 s = 1 min), konstruieren wir einen Umrechnungsfaktor, so dass die Einheit, die wir entfernen wollen, nämlich Minuten, im Zähler steht: 1 min/60 s. Anwenden und rechnen:
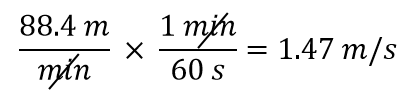
Beachte, dass die 88,4 automatisch in den Zähler kommt. Das liegt daran, dass jede Zahl im Zähler eines durch 1 geteilten Bruches stehen kann.
Teste dich selbst
Rechne 0,203 m/min in Meter/Sekunde um.
Antwort
0.00338 m/s oder 3,38 × 10-3 m/s
Abbildung 2.8 Wie schnell ist schnell?

Quelle: „Weinbergschnecke „von Jürgen Schoneris lizenziert unter der Creative Commons Attribution-Share Alike 3.0 Unported license.