Eine Konfusionsmatrix ist eine Tabelle, die häufig verwendet wird, um die Leistung eines Klassifizierungsmodells (oder „Klassifikators“) auf einem Satz von Testdaten zu beschreiben, für die die wahren Werte bekannt sind. Die Konfusionsmatrix selbst ist relativ einfach zu verstehen, aber die zugehörige Terminologie kann verwirrend sein.
Ich wollte eine „Kurzanleitung“ für die Terminologie der Konfusionsmatrix erstellen, weil ich keine bestehende Ressource finden konnte, die meinen Anforderungen entsprach: kompakte Darstellung, Verwendung von Zahlen anstelle von beliebigen Variablen und Erklärung sowohl in Form von Formeln als auch in Sätzen.
Beginnen wir mit einer Beispiel-Konfusionsmatrix für einen binären Klassifikator (obwohl sie leicht auf den Fall von mehr als zwei Klassen erweitert werden kann):
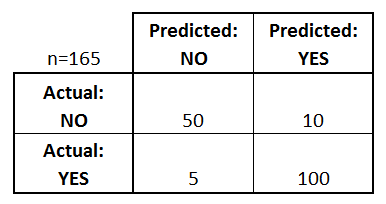
Was können wir aus dieser Matrix lernen?
- Es gibt zwei mögliche vorhergesagte Klassen: „Ja“ und „Nein“. Wenn wir zum Beispiel das Vorhandensein einer Krankheit vorhersagen, würde „ja“ bedeuten, dass sie die Krankheit haben, und „nein“ würde bedeuten, dass sie die Krankheit nicht haben.
- Der Klassifikator machte insgesamt 165 Vorhersagen (z.B., 165 Patienten wurden auf das Vorhandensein dieser Krankheit getestet).
- In diesen 165 Fällen sagte der Klassifikator 110 Mal „ja“ und 55 Mal „nein“ voraus.
- In Wirklichkeit haben 105 Patienten in der Stichprobe die Krankheit und 60 Patienten nicht.
Lassen Sie uns nun die grundlegendsten Begriffe definieren, bei denen es sich um ganze Zahlen (nicht um Raten) handelt:
- True Positives (TP): Das sind Fälle, bei denen wir ja vorhergesagt haben (sie haben die Krankheit), und sie haben die Krankheit.
- Wahr-Negative (TN): Wir haben Nein vorhergesagt, und sie haben die Krankheit nicht.
- Falsch-positive Fälle (FP): Wir haben ja vorhergesagt, aber die Person hat die Krankheit nicht. (Auch bekannt als „Fehler vom Typ I“)
- Falsch-negativ (FN): Wir haben „Nein“ vorhergesagt, aber die Person hat die Krankheit tatsächlich. (Auch bekannt als „Fehler vom Typ II“)
Ich habe diese Begriffe in die Konfusionsmatrix eingefügt und auch die Zeilen- und Spaltensummen hinzugefügt:
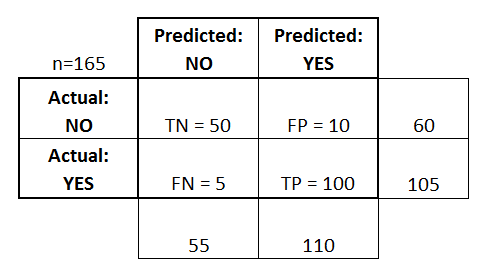
Dies ist eine Liste von Werten, die oft aus einer Konfusionsmatrix für einen binären Klassifikator berechnet werden:
- Genauigkeit: Wie oft liegt der Klassifikator insgesamt richtig?
- (TP+TN)/Gesamt = (100+50)/165 = 0,91
- Fehlklassifikationsrate: Wie oft ist sie insgesamt falsch?
- (FP+FN)/gesamt = (10+5)/165 = 0,09
- entspricht 1 minus Genauigkeit
- auch bekannt als „Fehlerrate“
- Rate der echten positiven Ergebnisse: Wenn es tatsächlich ja ist, wie oft sagt es ja voraus?
- TP/wirklich ja = 100/105 = 0,95
- auch bekannt als „Sensitivität“ oder „Recall“
- Falsch-Positiv-Rate: Wie oft wird ein Ja vorhergesagt, wenn es tatsächlich ein Nein ist?
- FP/eigentliches Nein = 10/60 = 0,17
- Rate der echten Negative: Wenn es tatsächlich nein ist, wie oft sagt es nein voraus?
- TN/tatsächlich nein = 50/60 = 0,83
- entspricht 1 minus Falsch-Positiv-Rate
- auch bekannt als „Spezifität“
- Präzision: Wenn sie ja vorhersagt, wie oft ist sie richtig?
- TP/vorgesagtes ja = 100/110 = 0,91
- Prävalenz: Wie oft tritt die Ja-Bedingung in unserer Stichprobe tatsächlich auf?
- Tatsächliches Ja/Gesamt = 105/165 = 0,64
Ein paar andere Begriffe sind ebenfalls erwähnenswert:
- Nullfehlerrate: Das ist die Häufigkeit, mit der man falsch liegen würde, wenn man immer die Mehrheitsklasse vorhersagen würde. (In unserem Beispiel wäre die Nullfehlerquote 60/165=0,36, denn wenn Sie immer „Ja“ vorhersagen würden, lägen Sie nur bei den 60 „Nein“-Fällen falsch.) Dies kann ein nützlicher Richtwert sein, mit dem Sie Ihren Klassifikator vergleichen können. Der beste Klassifikator für eine bestimmte Anwendung hat jedoch manchmal eine höhere Fehlerquote als die Null-Fehlerquote, wie das Genauigkeits-Paradoxon zeigt.
- Cohen’s Kappa: Dies ist im Wesentlichen ein Maß dafür, wie gut der Klassifikator im Vergleich zu dem Ergebnis ist, das er rein zufällig erzielt hätte. Mit anderen Worten, ein Modell hat einen hohen Kappa-Wert, wenn es einen großen Unterschied zwischen der Genauigkeit und der Null-Fehlerrate gibt. (Weitere Einzelheiten zu Cohens Kappa.)
- F-Score: Dies ist ein gewichteter Durchschnitt der wahren Positivrate (Recall) und der Präzision. (Weitere Informationen über den F-Score.)
- ROC-Kurve: Dies ist ein häufig verwendetes Diagramm, das die Leistung eines Klassifikators über alle möglichen Schwellenwerte zusammenfasst. Sie wird erstellt, indem die Rate der echten Positiven (y-Achse) gegen die Rate der falschen Positiven (x-Achse) aufgetragen wird, während Sie den Schwellenwert für die Zuordnung von Beobachtungen zu einer bestimmten Klasse variieren. (Weitere Einzelheiten zu ROC-Kurven.)
Und schließlich, für diejenigen unter Ihnen, die aus der Welt der Bayes’schen Statistik kommen, hier eine kurze Zusammenfassung dieser Begriffe aus Applied Predictive Modeling:
In Bezug auf die Bayes’sche Statistik sind die Sensitivität und Spezifität die bedingten Wahrscheinlichkeiten, die Prävalenz ist der Prior und die positiven/negativen vorhergesagten Werte sind die posterioren Wahrscheinlichkeiten.
Wollen Sie mehr erfahren?
In meinem neuen 35-minütigen Video, Making sense of the confusion matrix, erkläre ich diese Konzepte ausführlicher und decke fortgeschrittenere Themen ab:
- Wie man Präzision und Recall für Mehrklassenprobleme berechnet
- Wie man eine 10-Klassen-Konfusionsmatrix analysiert
- Wie man die richtige Bewertungsmetrik für sein Problem auswählt
- Warum die Genauigkeit oft eine irreführende Metrik ist
Lassen Sie mich wissen, wenn Sie Fragen haben!