Einführung
Die aktiven Stellen eines Enzyms bestehen in der Regel aus Aminosäureresten; je nachdem, welche Aminosäurereste vorhanden sind, kann die Spezifität des Substrats stark variieren. Je nach pH-Wert können sich die physikalischen Eigenschaften (hauptsächlich die elektrische Ladung) eines Enzyms ändern. Eine Veränderung der elektrischen Ladung kann die Wechselwirkung zwischen den Aminosäureresten im aktiven Zentrum und dem ankommenden Substrat verändern. So kann das Substrat über Wasserstoffbrückenbindungen oder Van-der-Waals-Kräfte an das aktive Zentrum binden. Sobald das Substrat an das aktive Zentrum bindet, bildet es einen Enzym-Substrat-Komplex, der dann an weiteren chemischen Reaktionen beteiligt ist.
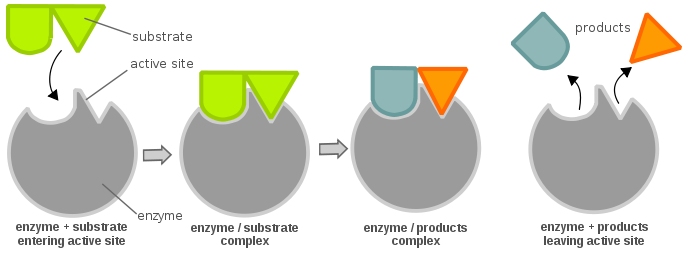
Damit ein Enzym aktiv und energetisch günstig ist, damit eine chemische Reaktion ablaufen kann, muss ein Substrat an die „aktive Stelle“ eines Enzyms binden. Eine aktive Stelle kann man sich wie ein Schloss und das Substrat wie einen Schlüssel vorstellen; dies ist als Schloss-Schlüssel-Modell bekannt. Ein Schlüssel (Substrat) muss eingeführt und gedreht werden (chemische Reaktion), dann öffnet sich das Schloss (Enzym) (Produktion von Produkten). Es ist zu beachten, dass ein Enzym mehr als eine aktive Stelle haben kann. Eine weitere Theorie über die Beziehung zwischen aktivem Ort und Substrat ist die Theorie der induzierten Passung, die das Gegenteil der Schlüssel-Schloss-Theorie ist (bei der der aktive Ort scheinbar unflexibel ist). Nach der Theorie der induzierten Anpassung ist die aktive Stelle des Enzyms sehr flexibel und ändert ihre Konformation nur, wenn das Substrat an sie bindet.
Enzyme wirken als Katalysator, indem sie die freie Gibbs-Energie der Aktivierung des Enzym-Substrat-Komplexes senken. Die folgenden zwei Abbildungen zeigen eine grundlegende enzymatische Reaktion mit und ohne Katalysator:
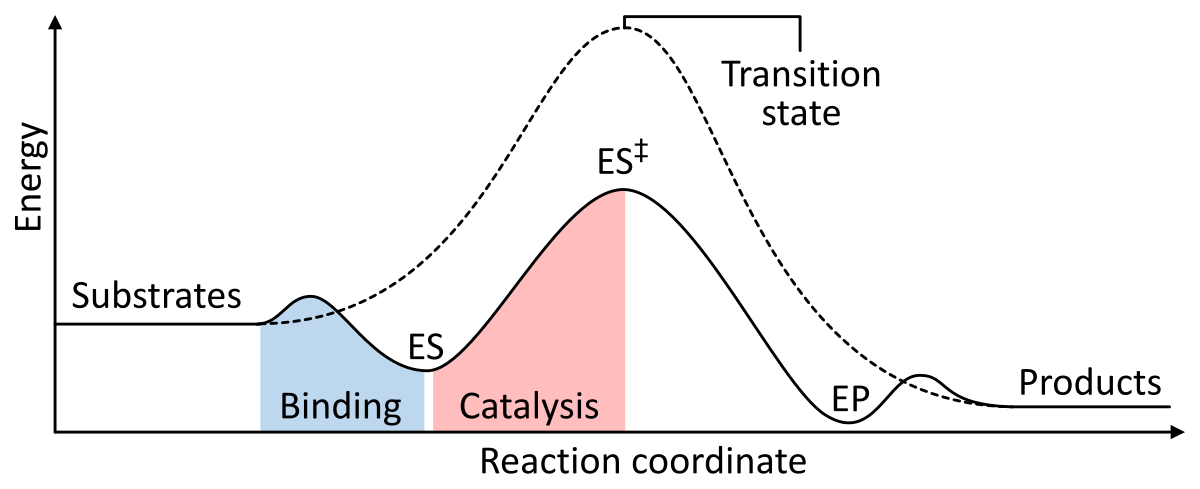
Abbildung 1: Die Energien der Phasen einer chemischen Reaktion. Unkatalysiert (gestrichelte Linie) benötigen die Substrate viel Aktivierungsenergie, um einen Übergangszustand zu erreichen, der dann in energieärmere Produkte zerfällt. Bei einer enzymkatalysierten Reaktion (durchgezogene Linie) bindet das Enzym die Substrate (ES) und stabilisiert dann den Übergangszustand (ES‡), um die Aktivierungsenergie zu verringern, die erforderlich ist, um Produkte (EP) zu erzeugen, die schließlich freigesetzt werden. aus Wikipedia.
Die Effizienz des Enzyms kann wie folgt bestimmt werden: Betrachten Sie eine einfache enzymatische Reaktion:
Die deutsche Biochemikerin Leonor Michaelis und die kanadische Biochemikerin Maud Menten leiteten eine Gleichung zur Beschreibung dieses Systems ab, die später als „Michaelis-Menten-Gleichung“ bekannt wurde und wie folgt aussieht:
\}{K_M + }
Diese Gleichung gibt die Reaktionsgeschwindigkeit bei einer gegebenen Substratkonzentration an, wobei Vmax, die maximale Geschwindigkeit, mit der die Reaktion ablaufen kann, und KM, die Michaelis-Konstante, als bekannt vorausgesetzt werden. Bei der praktischen Anwendung der Michaelis-Menten-Gleichung wird jedoch häufig V0 gemessen, und Vmax wird als Sättigung oder Plateau in einem Datenplot beobachtet. Da die Substratkonzentration bekannt ist, ist KM in der Regel der berechnete Wert von Interesse.
Für \(K_M\) wird angenommen, dass \(V_0= \dfrac{V_{max}}{2}\):
\}{K_M + } \tag{2}\]
\) \dfrac{V_{max}}{2} = V_{max} \tag{3}\]
\ = \dfrac{V_{max}}{\dfrac{V_{max}}{2}} \tag{4}
\ = 2 \tag{5}\]
\ \tag{6}\]
Die Michaelis-Konstante kann als die Geschwindigkeit angesehen werden, mit der das Substrat vom Enzym gelöst wird, was entweder in den Fällen geschehen kann, in denen der Substrat-Enzym-Komplex zum Produkt wird, oder das Substrat vom Enzym gelöst wird. KM kann als Gleichung dargestellt werden.
Wobei k-1 die Geschwindigkeitskonstante ist, bei der das Substrat nicht mehr an das Enzym gebunden ist, was zur Dissoziation des Enzym-Substrat-Komplexes führt, k2 die Geschwindigkeitskonstante ist, bei der der Substrat-Enzym-Komplex verschwindet und zum Produkt wird, und K1 die Geschwindigkeitskonstante für die Bildung des Substrat-Enzym-Komplexes ist. Daher kann KM als die Geschwindigkeit des Verschwindens des Substrat-Enzym-Komplexes geteilt durch die Geschwindigkeit der Bildung des Substrat-Enzym-Komplexes betrachtet werden, d. h. die Menge, bei der die Hälfte des Substrats an das Enzym gebunden ist. KM ist ein nützlicher Indikator für das Vorhandensein eines Hemmstoffs, da wir auf Veränderungen von KM achten und mit unserer Kontrolle vergleichen können (biologische Systeme, von denen wir wissen, dass kein Hemmstoff vorhanden ist). KM ist eine abhängige Variable, deren Wert sich aus vielen Gründen ändern kann, z. B. aufgrund des pH-Werts des Systems, der Temperatur oder anderer Bedingungen, die eine chemische Reaktion beeinflussen können. Ein kleiner KM-Wert zeigt an, dass das Substrat eine hohe Affinität für das Enzym hat.
Die Michaelis-Menten-Gleichung ist bei der Messung der Enzymeffizienz am nützlichsten, wenn v0 gegen , wie folgt aufgetragen wird:
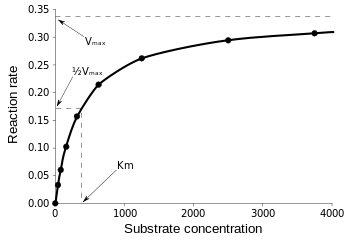
Abbildung 3: Diagramm der Reaktionsgeschwindigkeit und Michaelis-Menten-Konstante. aus Wikipedia.
Vmax ist die maximale Geschwindigkeit, mit der die Reaktion ablaufen kann, unabhängig von , d.h. selbst wenn man mehr Substrat hinzufügt, kann die Reaktion nicht schneller ablaufen. Das liegt daran, dass bei Vmax alle aktiven Stellen des Enzyms besetzt sind. Nach all den Erklärungen zu den verschiedenen Formen der kinetischen Gleichungen für Enzyme kommen wir zu unserer Schlussfolgerung bezüglich der katalytischen Effizienz. Zurückgehend auf Abb. 3 haben wir:
\_o}{\dfrac{k_{-1} + k_2}{k_1} + }\right) \tag{8}\]
Beachte, dass \(k_2\) im Vergleich zu k-1 und k1 eine irreversible Reaktion im Gegensatz zu einem Gleichgewichtsausdruck beschreibt. k2 ist hier auch als kcat bekannt, die katalytische Effizienz des Enzyms. Aus der vorangegangenen Diskussion geht hervor, dass v0 die gemessene Reaktionsgeschwindigkeit ist, d. h. die Produktbildung über die Zeit, so dass eine Gleichung wie folgt aussehen würde:
\}{dt} = k_2_0 \tag{9}\]
Wobei 0 die gesamte Enzymkonzentration ist.
Es ist auch bekannt, dass VMax beobachtet wird, wenn der gesamte Enzym-Substrat-Komplex verschwindet und sich in Produkte umwandelt, so dass wir die folgende Annahme machen können:
\_0 \tag{10} \]
und nach der Umordnung haben wir diese Gleichung:
\_0} \tag{11}\]
Das ist die Gleichung für die Berechnung der katalytischen Effizienz, die wir verwenden, nachdem wir Daten aus Experimenten erhalten und die Michaelis-Menten-Gleichung verwendet haben. Bei einem größeren kcat ist das Enzym effizient, weil weniger Enzym benötigt wird.