Kompressibilitätsfaktor (Gase) - Knowino

Von Knowino

Dies ist eine geprüfte Version dieser Seite

Springen zu: Navigation, Suche

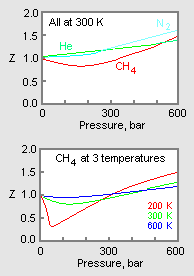
Abbildung 1: Beispielgrafiken von Gaskompressibilitätsfaktoren

Der Kompressibilitätsfaktor (Z) ist eine nützliche thermodynamische Eigenschaft zur Modifizierung des idealen Gasgesetzes, um das Verhalten von realen Gasen zu berücksichtigen. Er ist ein Maß dafür, wie stark die thermodynamischen Eigenschaften eines realen Gases von denen abweichen, die man von einem idealen Gas erwartet. Man kann es sich als das Verhältnis des tatsächlichen Volumens eines realen Gases zu dem vom idealen Gas vorhergesagten Volumen bei gleicher Temperatur und gleichem Druck wie das tatsächliche Volumen vorstellen.

Für ein ideales Gas hat Z immer den Wert 1. Für reale Gase kann der Wert positiv oder negativ abweichen, je nach der Wirkung der intermolekularen Kräfte des Gases. Je näher ein reales Gas an seinem kritischen Punkt oder an seinem Sättigungspunkt ist, desto größer sind die Abweichungen des Gases vom idealen Verhalten.

Das obere Diagramm in Abbildung 1 zeigt, wie der Kompressibilitätsfaktor für verschiedene Gase bei gleicher Temperatur und gleichem Druck variiert. Das untere Diagramm zeigt, wie der Kompressibilitätsfaktor eines Gases (z. B. Methan) bei einem bestimmten Druck mit der Temperatur variiert.

Dieser Artikel befasst sich nur mit dem Kompressibilitätsfaktor von Gasen und geht nicht auf die Kompressibilität von Flüssigkeiten oder Dampf-Flüssigkeits-Gemischen ein.

Inhalt

1 Bestimmung von Gaskompressibilitätswerten
- 1.1 Verallgemeinerte Kompressibilitätsfaktordiagramme für reine Gase
- 1.2 Verallgemeinerte Kompressibilitätsfaktordiagramme für Gasgemische
- 1.3 Die van-der-Waals-Gleichung
  - 1.3.1 Modifizierte Versionen der van-der-Waals-Gleichung
    - 1.3.1.1 Redlich-Kwong
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
- 1.4 Viriale Zustandsgleichung
- 1.5 Andere Zustandsgleichungen
- 1.6 Notation der Gaskonstante
2 Literaturhinweise

Bestimmung der Kompressibilitätswerte von Gasen

Das ideale Gasgesetz ist definiert als:

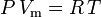
$P\,V_\mathrm{m} = R\,T$

und das um Nicht-Idealität korrigierte ideale Gasgesetz ist definiert als:

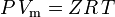
$P\,V_\mathrm{m} = ZR\,T$

wobei:
P	= Druck
Vm	= molares Volumen des Gases
Z	= Kompressibilitätsfaktor
R	= Universelle Gaskonstante
T	= Temperatur

und somit:

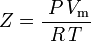
$Z = \frac{\;P\,V_\mathrm{m}}{R\,T}$

, was die einfachste und am weitesten verbreitete Zustandsgleichung für reale Gase (EOS) ist. Die größte Einschränkung dieser Zustandsgleichung besteht darin, dass der Gaskompressibilitätsfaktor Z keine Konstante ist, sondern von einem Gas zum anderen sowie mit der Temperatur und dem Druck des betrachteten Gases variiert. Er muss experimentell bestimmt werden.

Wenn experimentelle Daten für bestimmte Gase zur Verfügung stehen, können diese Daten verwendet werden, um Diagramme (wie in Abbildung 1) von Z gegen den Druck bei einer konstanten Temperatur oder von Z gegen den Druck für verschiedene Temperaturen für diese spezifischen Gase zu erstellen. Solche Diagramme sind nützlich, um leicht interpolierte Werte von Z zwischen den experimentell bestimmten Werten zu erhalten.

Der Kompressibilitätsfaktor kann, wie bereits erwähnt, auch wie folgt ausgedrückt werden:

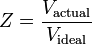
$Z = \frac{V_\mathrm{Ist}}{V_\mathrm{Ideal}}$

Es gibt drei Regime, die den Kompressibilitätsfaktor beeinflussen:

Der Wert von Z tendiert gegen 1, wenn der Gasdruck sich 0 nähert, der Wert von Z ist bei mittleren Drücken kleiner als 1, weil die zwischenmolekularen Anziehungskräfte dazu führen, dass die tatsächlichen Volumina kleiner sind als die idealen Werte
der Wert von Z ist größer als 1 und tendiert schließlich gegen unendlich bei hohen Drücken, weil die zwischenmolekularen Abstoßungskräfte bewirken, dass die tatsächlichen Volumina größer sind als die idealen Werte

Verallgemeinerte Kompressibilitätsfaktor-Diagramme für reine Gase

Die eindeutige Beziehung zwischen dem Kompressibilitätsfaktor und der reduzierten Temperatur, Tr, und dem reduzierten Druck, Pr, wurde erstmals 1873 von van der Waals erkannt und ist als Zwei-Parameter-Prinzip der korrespondierenden Zustände bekannt. Das Prinzip der korrespondierenden Zustände drückt die Verallgemeinerung aus, dass die Eigenschaften eines Gases, die von den zwischenmolekularen Kräften abhängen, mit den kritischen Eigenschaften des Gases in einer universellen Weise zusammenhängen. Dies ist eine wichtige Grundlage für die Entwicklung von Korrelationen zwischen molekularen Eigenschaften.

In Bezug auf die Kompressibilität von Gasen besagt das Prinzip der korrespondierenden Zustände, dass jedes reine Gas bei der gleichen reduzierten Temperatur, Tr, und dem gleichen reduzierten Druck, Pr, den gleichen Kompressibilitätsfaktor haben sollte.

Die reduzierte Temperatur und der reduzierte Druck sind definiert als:

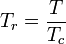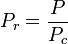
$T_r = \frac{T}{T_c}$ und $P_r = \frac{P}{P_c}$

Tc und Pc sind bekannt als die kritische Temperatur und der kritische Druck eines Gases. Tc ist die Temperatur, oberhalb derer es nicht möglich ist, ein bestimmtes Gas zu verflüssigen, und Pc ist der Mindestdruck, der erforderlich ist, um ein bestimmtes Gas bei seiner kritischen Temperatur zu verflüssigen. Zusammen definieren sie den kritischen Punkt eines Fluids, oberhalb dessen es keine getrennten flüssigen und gasförmigen Phasen eines bestimmten Fluids gibt.

Die Druck-Volumen-Temperatur-Daten (PVT) für reale Gase variieren von einem reinen Gas zum anderen. Wenn jedoch die Kompressibilitätsfaktoren verschiedener Einkomponentengase zusammen mit Temperaturisothermen gegen den Druck aufgetragen werden (wie für Methan im unteren Diagramm von Abbildung 1 gezeigt), weisen viele der Diagramme ähnliche Isothermenformen auf.

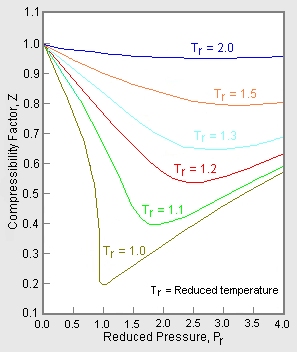
Abbildung 2: Beispiel eines verallgemeinerten Kompressibilitätsfaktordiagramms

Um ein verallgemeinertes Diagramm zu erhalten, das für viele verschiedene Gase verwendet werden kann, werden der reduzierte Druck und die reduzierte Temperatur, Pr und Tr, zur Normalisierung der Kompressibilitätsfaktordaten verwendet. Abbildung 2 ist ein Beispiel für ein verallgemeinertes Kompressibilitätsfaktor-Diagramm, das aus Hunderten von experimentellen P-V-T-Datenpunkten von 10 reinen Gasen abgeleitet wurde, nämlich Methan, Ethan, Ethylen, Propan, n-Butan, i-Pentan, n-Hexan, Stickstoff, Kohlendioxid und Dampf.

Es gibt detailliertere verallgemeinerte Kompressibilitätsfaktor-Diagramme, die auf 25 oder mehr verschiedenen reinen Gasen basieren, wie z. B. die Nelson-Obert-Diagramme. Solche Diagramme haben eine Genauigkeit von 1-2 % für Z-Werte über 0,6 und von 4-6 % für Z-Werte von 0,3-0,6.

Die verallgemeinerten Kompressibilitätsfaktor-Diagramme können bei stark polaren Gasen, d. h. bei Gasen, bei denen die Zentren der positiven und negativen Ladung nicht zusammenfallen, beträchtliche Fehler aufweisen. In solchen Fällen kann die Schätzung für Z um bis zu 15-20 % falsch sein.

Die Quantengase Wasserstoff, Helium und Neon entsprechen nicht dem Verhalten der korrespondierenden Zustände, und der reduzierte Druck und die reduzierte Temperatur für diese drei Gase sollten wie folgt neu definiert werden, um die Genauigkeit der Vorhersage ihrer Kompressibilitätsfaktoren bei Verwendung der verallgemeinerten Diagramme zu verbessern:

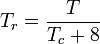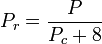
$T_r = \frac{T}{T_c + 8}$ und $P_r = \frac{P}{P_c + 8}$

wobei die Temperaturen in Grad Kelvin und die Drücke in Atmosphären angegeben sind.

Verallgemeinerte Kompressibilitätsfaktor-Diagramme für Gasgemische

Die verallgemeinerten Kompressibilitätsfaktor-Diagramme für reine Gase (wie in Abbildung 2 dargestellt) oder die Nelson-Obert-Diagramme können auch für Gasgemische verwendet werden, indem die von W. B. Kay 1936 vorgeschlagene Kay-Regel verwendet wird. Diese Regel sagt das P-V-T-Verhalten eines Gasgemisches voraus, indem sie den Kompressibilitätsfaktor für ein Gasgemisch bei der reduzierten Temperatur und dem reduzierten Druck bestimmt, die durch die pseudokritische Temperatur Tpc und den pseudokritischen Druck Ppc definiert sind, die wie folgt definiert sind:

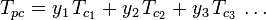
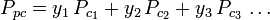
$T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_2} + y_3\,T_{c_3}\,\dots$ $P_{pc} = y_1\,P_{c_1} + y_2\,P_{c_2} + y_3\,P_{c_3}\,\dots$

wobei:
Tpc	= die pseudokritische Temperatur des Gasgemisches
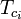$T_{c_i}$	= die kritische Temperatur einer Komponente des Gasgemisches
Ppc	= der pseudokritische Druck des Gasgemisches
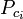$P_{c_i}$	= die kritische Temperatur einer Komponente des Gases
yi	= der Mol- (oder Volumen-) Anteil einer Komponente des Gases

Die pseudoreduzierte Temperatur, Tpr, und der pseudoreduzierte Druck, Ppr, zur Verwendung mit den verallgemeinerten Kompressibilitätsfaktordiagrammen für reine Gase sind dann:

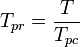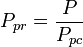
$T_{pr} = \frac{T}{T_{pc}}$ und $P_{pr} = \frac{P}{P_{pc}}$

Ein Kompressibilitätsfaktor-Diagramm für Erdgas (das ein Gemisch aus Kohlenwasserstoff und anderen Gasen ist) unter Verwendung pseudoreduzierter Temperaturen und Drücke ist im Internet verfügbar.

Die van-der-Waals-Gleichung

Die van-der-Waals-Gleichung wurde 1873 entwickelt und kann wie folgt ausgedrückt werden:

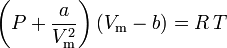
$\left(P + \frac{a}{V_\mathrm{m}^2}\right)\left(V_\mathrm{m} - b\right) = R\,T$

wobei:

a ist ein Maß für die Anziehungskraft zwischen den Gasmolekülen b berücksichtigt das von den Gasmolekülen eingenommene Volumen, was das verfügbare offene Volumen verringert

Die van-der-Waals-Gleichung kann umgestellt werden als:

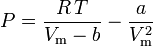
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

und der Kompressibilitätsfaktor kann geschrieben werden als:

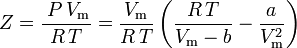
$Z = \frac{\;P\,V_\mathrm{m}}{R\,T} = \frac{V_\mathrm{m}}{R\,T}\left(\frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2}\right)$

und wir haben nun eine Gleichung zur Bestimmung von Z unter Verwendung der van der Waals Parameter a und b:

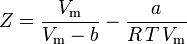
$Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}$

Obwohl a und b als „Van-der-Waals-Konstanten“ bezeichnet werden, sind sie keine wirklichen Konstanten, da sie von einem Gas zum anderen variieren; sie sind jedoch unabhängig von P, V und T. Mit anderen Worten: Sie sind für das betrachtete Gas konstant. Angesichts der kritischen Temperatur und des kritischen Drucks für ein bestimmtes Gas lassen sich a und b für dieses spezifische Gas aus diesen Gleichungen ableiten:

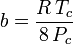
$a = \frac{27\, R^2\, T_c^2}{64\, P_c}$ und $b = \frac{R\, T_c}{8\, P_c}$

Zum Beispiel beträgt der kritische Druck von Ethan 4.884 MPa und die kritische Temperatur beträgt 305,43 K (32,3˚C). Unter Verwendung der universellen Gaskonstante R von 8,3145 Pa m3 K-1 mol-1 ergeben die obigen Gleichungen a = 0,557 m6 Pa mol-2 und b = 6,500×10-5 m3 mol-1.

Tabellierte Werte von a und b für verschiedene Gase sind in diesen Referenzen sowie in vielen anderen Quellen der Fachliteratur verfügbar.

Modifizierte Versionen der van-der-Waals-Gleichung

Die Bestimmung der Kompressibilitätsfaktoren mit Hilfe der van-der-Waals-Zustandsgleichung ist eine Verbesserung gegenüber der Verwendung der verallgemeinerten Kompressibilitätskarten. Es gibt jedoch modifizierte Versionen der van-der-Waals-Zustandsgleichung, die noch mehr Verbesserungen bieten. Die von Ingenieuren, die in der Erdölraffination, der petrochemischen Produktion, der Erdgasverarbeitung, der kryogenen Destillation und verwandten Industriezweigen arbeiten, vielleicht am häufigsten verwendeten Zustandsgleichungen sind: die 1949 entwickelte Redlich-Kwong-Gleichung, die 1972 entwickelte Soave-Redlich-Kwong-Gleichung und die 1976 entwickelte Peng-Robinson-Gleichung. Diese drei Gleichungen sind im Wesentlichen modifizierte Versionen der van-der-Waals-Gleichung. Die vergleichenden Gleichungen sind:

Redlich-Kwong

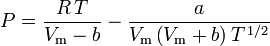
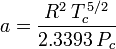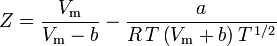
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)T^{\,1/2}}$ $a = \frac{R^2\, T_c^{\,5/2}}{2.3393\, P_c}$ und $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{\,1/2}}$

Soave-Redlich-Kwong

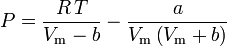
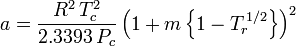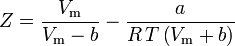
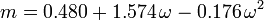
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\links(V_\mathrm {m} + b\rechts)}$ $a = \frac{R^2\,T_c^2}{2.3393\,P_c}\, \Big(1 + m\, \Big\{1 - T_r^{\,1/2} \Big\} \Big)^2$ und $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)}$ $m = 0.480 + 1,574\, \omega - 0,176\, \omega^2$

Der akzentrische Faktor ω, der als Parameter in den Soave-Redlich-Kwong- und Peng-Robinson-Gleichungen verwendet wird, wurde erstmals 1955 von Pitzer et al. eingeführt. Er kann wie folgt ausgedrückt werden:

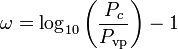
$\omega = \log_{10} \left(\frac{P_c}{P_\mathrm{vp}}\right) - 1$

wobei Pvp der Sättigungsdampfdruck des Gases bei einer Temperatur von 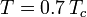$T = 0,7\, T_c$ ist.

Peng-Robinson

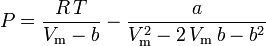
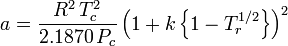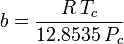
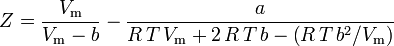
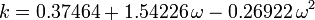
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}\, b - b^2}$ $a = \frac{R^2\,T_c^2}{2.1870\,P_c}\, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big)^2$ und $b = \frac{R\, T_c}{12.8535\, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m} + 2\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)}$ $k = 0,37464 + 1,54226\, \omega - 0,26922\, \omega^2$

Viriale Zustandsgleichung

Die grundlegendste Zustandsgleichung, da sie die solideste theoretische Grundlage hat, ist die viriale Zustandsgleichung:

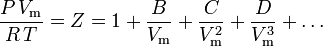
$\frac{P\,V_\mathrm{m}}{R\,T} = Z = 1 + \frac{B}{V_\mathrm{m}} + \frac{C}{V_\mathrm{m}^2} + \frac{D}{V_\mathrm{m}^3} + \dots$

Er wurde erstmals 1885 von Thiesen auf empirischer Basis vorgeschlagen und 1901 von Kamerlingh-Onnes weiterentwickelt. Ein statistisch-mechanischer Ausdruck für B wurde erstmals von Ornstein in seiner Dissertation abgeleitet. Die Gleichung wurde anschließend von H.D. Ursell 1927 auf einer theoretischen Grundlage weiterentwickelt, die aus einer statistisch-mechanischen (Cluster-)Analyse der zwischenmolekularen Kräfte abgeleitet wurde.

Die Parameter B, C und D werden als zweiter, dritter bzw. vierter Virialkoeffizient bezeichnet. Die Koeffizienten sind keine Konstanten, da sie von einem Gas zum anderen sowie von der Temperatur des betrachteten Gases abhängen. Sie werden manchmal als B(T), C(T) und D(T) geschrieben, um zu verdeutlichen, dass sie Funktionen der Temperatur sind. Der numerische Wert der Koeffizienten muss experimentell bestimmt werden.

Der zweite Virialkoeffizient liefert den größten Teil der Korrektur für das nicht-ideale Verhalten eines Gases. Aus diesem Grund wird die Virialgleichung manchmal nach dem Term, der den zweiten Koeffizienten enthält, abgekürzt. Wenn jedoch der dritte Koeffizient verfügbar ist, wird die Gleichung in der Regel nach dem Term mit dem dritten Koeffizienten abgeschnitten. Der vierte Koeffizient ist nur selten verfügbar.

Eine umfangreiche Zusammenstellung von Virialkoeffizienten für reine Gase und Gasgemische wurde aus der Virialkoeffizientendatenbank des Thermodynamics Research Center erstellt, das früher an der Texas A&M University, College Station, Texas, angesiedelt war und jetzt am National Institute of Standards and Technology (NIST), Boulder, Colorado, angesiedelt ist. Die letzte Version dieser Zusammenstellung wurde 2003 veröffentlicht. Das NIST bietet auch ein Softwareprogramm zum Kauf an, die NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), die den zweiten und dritten Virialkoeffizienten sowie eine Vielzahl anderer thermodynamischer Eigenschaften enthält.

Andere Zustandsgleichungen

Es gibt eine Reihe anderer Zustandsgleichungen zur Vorhersage des Verhaltens realer Gase. Die vielleicht bekanntesten sind die 1929 entwickelte Beattie-Bridgeman-Gleichung und die 1940 entwickelte Benedict-Rubin-Webb-Gleichung. Im Allgemeinen sind sie komplexer als die oben genannten Gleichungen.

Notation für die Gaskonstante

Die in diesem Artikel verwendete Gaskonstante ist die universelle Gaskonstante R, die für jedes Gas gilt. Es gibt auch eine spezifische Gaskonstante, die als Rs bezeichnet werden kann und definiert ist als Rs = R / M, wobei M das Molekulargewicht ist.

Unglücklicherweise verwenden viele Autoren in der Fachliteratur manchmal R als spezifische Gaskonstante, ohne sie als solche zu bezeichnen oder anzugeben, dass es sich um die spezifische Gaskonstante handelt. Dies kann und wird zu Verwirrung führen.

1.0 1.1 1.2 1.3 1.4 McQuarrie, Donald A. und Simon, John D. (1999). Molecular Thermodynamics. University Science Books. ISBN 1-891389-05-X.
2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal und Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, 2. Auflage. McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Introduction to Chemical Engineering Thermodynamics, Seventh Edition. McGraw Hill. ISBN 0-07-310445-0.
4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Chemical Engineering Thermodynamics. Universities Press (Indien). ISBN 81-7371-048-1.
5.0 5.1 Gasgesetze (Vortrag von Professor M.J. Mombourquette an der Queens University, Kanada)
Hong Wei Xiang (2005). Das Prinzip der korrespondierenden Zustände und seine Praxis: Thermodynamische, Transport- und Oberflächeneigenschaften von Fluiden. Elsevier. ISBN 0-444-52062-7.
IUPAC Goldbook
Gouq-Jen Su (1946). „Modified Law of Corresponding States“. Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.
9.0 9.1 Zustandsgleichungen (Professor Lyes Kadem, Concordia University, Canada)
10.0 10.1 Zustandsgleichungen (Vorlesungsmaterial von Professor Sanford Klein an der University of Wisconsin-Madison, U.S.)
Richard W. Miller (1996). Flow Measurement Engineering Handbook, 3. Auflage. McGraw-Hill. ISBN 0-07-042366-0. (Siehe Abbildung G-1 auf Seite G.145)
Kai-Fui Vincent Wong (2000). Thermodynamics for Engineers, 1st Edition. CRC Press. ISBN 0-8493-0232-3. (Siehe Abbildung A-2, Seite 278}
Nelson-Obert Generalized Compressibility Charts (Charts verfügbar im Internet, von der Website der San Diego State University, U.S.)
W.B.Kay (1936). „Gase und Dämpfe bei hoher Temperatur und hohem Druck – Dichte der Kohlenwasserstoffe“. Wirtschaftsingenieurwesen & Chemie 28:1014. ISSN 0096-4484.
Yunus A. Çengal und Michael A. Bowes (2005). Thermodynamics: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
Real Gases (Vorlesungsmaterial von Professor R.M. Price an der Christian Brothers University, U.S.A.)
Properties of Natural Gases (Professor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
Robert C. Weast (Editor) (1975). Handbook of Chemistry and Physics, 56th Edition. CRC Press. ISBN 0-87819-455-X.
19.0 19.1 19.2 Kapitel 3: Zustandsgleichungen (Seiten 6-8 von 65 pdf-Seiten) (Teil der Dissertation von Ji Lin Wang, 2002, Swinbourne University of Technology, Australien)
20.0 20.1 20.2 Jean Vidal (2003). Thermodynamics: Applications in Chemical Engineering and the Petroleum Industry. Editions Technip. ISBN 2-7108-0800-5.
Zakia Nasri und Housam Binous (2007). „Applications of the Soave-Redlich-Kwong Equation of State Using Mathematica“. Journal of Chemical Engineering of Japan 40 (6): 534-538. Retrieved from here.
K.S. Pitzer et al (1955). „The Volumetric and Thermodynamic Properties of Fluids“. Journal of the American Chemical Society 77: 3427-3440.
Francis S. Manning und Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
Definition des akzentrischen Faktors (Physical Property Sources Index, PPSI, der Eidgenössischen Technischen Hochschule Zürich)
Max F. Thiesen (1885). „Untersuchungen über die Zustandsgleichung“. Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901). „Ausdruck der Zustandsgleichung von Gasen und Flüssigkeiten durch Reihen“. Commun. Phys. Lab. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistischen mechanica van Gibbs op molekulair-theoretische vraagstukken (Anwendung der statistischen Mechanik von Gibbs auf molekulartheoretische Probleme), Leiden
H. D. Ursell (1927). „Die Auswertung des Gibbsschen Phasenintegrals für unvollkommene Gase“ (23): 685.
J.D. Dymond and R.C. Wilhoit (Authors), K.N. Marsch and M. Fenkel (Editors) (2003). Virialkoeffizienten von reinen Gasen und Gemischen, 1. Auflage. Springer. ISBN 3-540-44340-1.
NIST Standard Reference Database 23
J.A. Beattie und O.C. Bridgeman (1929). „A New Equation of State for Fluids“. Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb und L.C. Rubin (1940). „An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures“. J. Chem. Phys. 8: 334-335.

Einige Inhalte auf dieser Seite sind möglicherweise bereits auf Citizendium erschienen.

Abgerufen von „http://knowino.org/wiki/Compressibility_factor_(gases)“

Kategorie: Physik