Ein zellularer Automat ist eine Ansammlung von „farbigen“ Zellen auf einem Gitter bestimmter Form, die sich in einer Reihe von diskreten Zeitschritten gemäß einer Reihe von Regeln entwickelt, die auf den Zuständen benachbarter Zellen basieren. Die Regeln werden dann iterativ für so viele Zeitschritte wie gewünscht angewandt. von Neumann war einer der ersten, der ein solches Modell in Betracht zog und ein zelluläres Modell in seinen „universellen Konstruktor“ einbaute. Zelluläre Automaten wurden in den frühen 1950er Jahren als ein mögliches Modell für biologische Systeme untersucht (Wolfram 2002, S. 48). Umfassende Studien zu zellulären Automaten wurden von S. Wolfram ab den 1980er Jahren durchgeführt, und Wolframs grundlegende Forschungen auf diesem Gebiet gipfelten in der Veröffentlichung seines Buches A New Kind of Science (Wolfram 2002), in dem Wolfram eine gigantische Sammlung von Ergebnissen zu Automaten vorstellt, darunter eine Reihe von bahnbrechenden Neuentdeckungen.
In der Episode „Bettor or Worse“ (2006) der zweiten Staffel des Fernsehkrimis NUMB3RS werden eindimensionale zelluläre Automaten erwähnt.
Zelluläre Automaten gibt es in einer Vielzahl von Formen und Varianten. Eine der grundlegendsten Eigenschaften eines zellulären Automaten ist die Art des Gitters, auf dem er berechnet wird. Das einfachste dieser „Gitter“ ist eine eindimensionale Linie. In zwei Dimensionen können quadratische, dreieckige und sechseckige Gitter in Betracht gezogen werden. Zelluläre Automaten können auch auf kartesischen Gittern in einer beliebigen Anzahl von Dimensionen konstruiert werden, wobei das 
-dimensionale ganzzahlige Gitter 
die häufigste Wahl ist. Zelluläre Automaten auf einem 
-dimensionalen ganzzahligen Gitter sind in der Wolfram Language als CellularAutomaton implementiert.
Die Anzahl der Farben (oder unterschiedlichen Zustände) 
, die ein zellulärer Automat annehmen kann, muss ebenfalls angegeben werden. Diese Zahl ist normalerweise eine ganze Zahl, wobei 
(binär) die einfachste Wahl ist. Bei einem binären Automaten wird die Farbe 0 allgemein als „weiß“ und die Farbe 1 allgemein als „schwarz“ bezeichnet. Es können jedoch auch zelluläre Automaten mit einem kontinuierlichen Bereich möglicher Werte in Betracht gezogen werden.
Neben dem Gitter, auf dem ein zellulärer Automat lebt, und den Farben, die seine Zellen annehmen können, muss auch die Umgebung angegeben werden, in der sich die Zellen gegenseitig beeinflussen. Die einfachste Wahl ist die „nächste Nachbarschaft“, in der nur Zellen, die direkt an eine bestimmte Zelle angrenzen, bei jedem Zeitschritt beeinflusst werden können. Zwei gängige Nachbarschaften im Falle eines zweidimensionalen zellulären Automaten auf einem quadratischen Gitter sind die sogenannte Moore-Nachbarschaft (eine quadratische Nachbarschaft) und die von-Neumann-Nachbarschaft (eine rautenförmige Nachbarschaft).
Der einfachste Typ eines zellulären Automaten ist ein binärer, eindimensionaler Automat mit den nächsten Nachbarn. Solche Automaten wurden von S. Wolfram als „elementare zelluläre Automaten“ bezeichnet, der ihre erstaunlichen Eigenschaften eingehend untersucht hat (Wolfram 1983; 2002, S. 57). Es gibt 256 solcher Automaten, von denen jeder durch eine eindeutige Binärzahl indiziert werden kann, deren dezimale Darstellung als „Regel“ für den jeweiligen Automaten bekannt ist. Eine Illustration der Regel 30 ist oben zusammen mit der Entwicklung gezeigt, die sie nach 15 Schritten ausgehend von einer einzelnen schwarzen Zelle hervorbringt.
Eine etwas kompliziertere Klasse von zellulären Automaten sind die eindimensionalen totalistischen zellulären Automaten mit 
-Farben und nächstem Nachbarn. In solchen Automaten bestimmt der Durchschnitt der benachbarten Zellen die Entwicklung, und die einfachsten nichttrivialen Beispiele haben 
Farben. Bei diesen Automaten kann die Menge der Regeln, die das Verhalten beschreiben, als 
-stellige 
-Zahl kodiert werden, die als „Code“ bekannt ist. Die Regeln und 300 Schritte des ternären (
) Code 912-Automaten sind oben abgebildet.
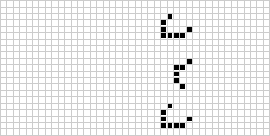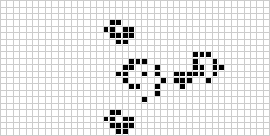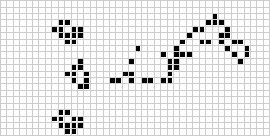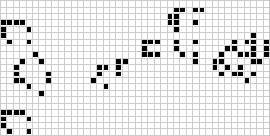
Der bekannteste zelluläre Automat in zwei Dimensionen ist Conways Spiel des Lebens, das 1970 von J. H. Conway entdeckt und in Martin Gardners Scientific American-Kolumnen popularisiert wurde. Das Spiel des Lebens ist ein binärer (
) totalistischer zellulärer Automat mit einer Moore-Nachbarschaft des Bereichs 
. Obwohl die Berechnung der aufeinanderfolgenden Generationen des Spiels des Lebens ursprünglich von Hand erfolgte, hielt die Computerrevolution bald Einzug und ermöglichte es, umfangreichere Muster zu untersuchen und zu propagieren.
WireWorld ist ein weiterer gängiger zweidimensionaler zellulärer Automat.
Die Theorie der zellulären Automaten ist sehr reichhaltig, da einfache Regeln und Strukturen eine große Vielfalt an unerwarteten Verhaltensweisen hervorbringen können. So gibt es zum Beispiel universelle zelluläre Automaten, die in der Lage sind, das Verhalten jedes anderen zellulären Automaten oder jeder Turing-Maschine zu simulieren. Gacs (2001) hat sogar bewiesen, dass es fehlertolerante universelle zelluläre Automaten gibt, deren Fähigkeit, andere zelluläre Automaten zu simulieren, durch zufällige Störungen nicht beeinträchtigt wird, vorausgesetzt, diese Störungen sind hinreichend spärlich.