Un autómata celular es una colección de celdas «coloreadas» en una cuadrícula de forma específica que evoluciona a través de un número de pasos de tiempo discreto de acuerdo con un conjunto de reglas basadas en los estados de las celdas vecinas. Las reglas se aplican entonces de forma iterativa durante tantos pasos de tiempo como se desee. von Neumann fue uno de los primeros en considerar un modelo de este tipo, e incorporó un modelo celular a su «constructor universal». Los autómatas celulares se estudiaron a principios de la década de 1950 como un posible modelo para los sistemas biológicos (Wolfram 2002, p. 48). S. Wolfram realizó estudios exhaustivos de los autómatas celulares a partir de la década de 1980, y la investigación fundamental de Wolfram en este campo culminó con la publicación de su libro A New Kind of Science (Wolfram 2002), en el que Wolfram presenta una gigantesca colección de resultados relativos a los autómatas, entre los que se encuentran una serie de nuevos descubrimientos revolucionarios.
El episodio de la segunda temporada «Bettor or Worse» (2006) de la serie policíaca de televisión NUMB3RS menciona los autómatas celulares unidimensionales.
Los autómatas celulares tienen diversas formas y variedades. Una de las propiedades más fundamentales de un autómata celular es el tipo de cuadrícula en la que se calcula. La «cuadrícula» más sencilla es una línea unidimensional. En dos dimensiones, pueden considerarse rejillas cuadradas, triangulares y hexagonales. Los autómatas celulares también pueden construirse sobre rejillas cartesianas de un número arbitrario de dimensiones, siendo la retícula de números enteros de 
dimensiones 
la opción más común. Los autómatas celulares en un entramado entero 
-dimensional se implementan en Wolfram Language como CellularAutomaton.
También se debe especificar el número de colores (o estados distintos) 
que puede asumir un autómata celular. Este número suele ser un entero, siendo 
(binario) la opción más sencilla. Para un autómata binario, el color 0 se llama comúnmente «blanco», y el color 1 se llama comúnmente «negro». Sin embargo, también se pueden considerar autómatas celulares que tengan un rango continuo de valores posibles.
Además de la cuadrícula en la que vive un autómata celular y los colores que pueden asumir sus celdas, también se debe especificar la vecindad sobre la que las celdas se afectan entre sí. La opción más sencilla es la de «vecinos más cercanos», en la que sólo las celdas directamente adyacentes a una celda dada pueden verse afectadas en cada paso de tiempo. Dos vecindades comunes en el caso de un autómata celular bidimensional en una cuadrícula cuadrada son la llamada vecindad de Moore (una vecindad cuadrada) y la vecindad de von Neumann (una vecindad en forma de diamante).
El tipo más simple de autómata celular es un autómata unidimensional binario, de vecino más cercano. Estos autómatas fueron llamados «autómatas celulares elementales» por S. Wolfram, que ha estudiado ampliamente sus sorprendentes propiedades (Wolfram 1983; 2002, p. 57). Existen 256 autómatas de este tipo, cada uno de los cuales puede ser indexado por un único número binario cuya representación decimal se conoce como la «regla» del autómata en cuestión. Una ilustración de la regla 30 se muestra arriba junto con la evolución que produce después de 15 pasos a partir de una sola celda negra.
Una clase ligeramente más complicada de autómatas celulares son los autómatas unidimensionales totalistas de vecino más cercano, 
. En estos autómatas, es el promedio de las celdas adyacentes el que determina la evolución, y los ejemplos más simples no triviales tienen 
colores. Para estos autómatas, el conjunto de reglas que describen el comportamiento puede codificarse como un número de 
dígitos 
conocido como «código». Las reglas y los 300 pasos del autómata ternario (
) de código 912 se ilustran más arriba.
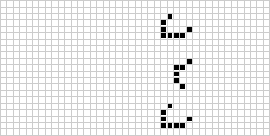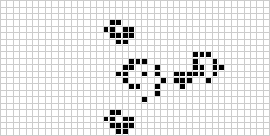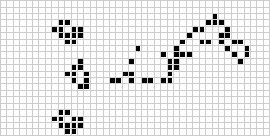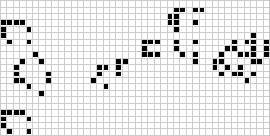
En dos dimensiones, el autómata celular más conocido es el juego de la vida de Conway, descubierto por J. H. Conway en 1970 y popularizado en las columnas de Scientific American de Martin Gardner. El juego de la vida es un autómata celular totalista binario (
) con una vecindad de Moore de rango 
. Aunque el cómputo de las sucesivas generaciones del juego de la vida se hacía originalmente a mano, la revolución informática llegó pronto y permitió estudiar y propagar patrones más extensos. Más arriba se ilustra una animación de la construcción del juego de la vida conocido como tren hinchable.
WireWorld es otro autómata celular bidimensional común.
La teoría de los autómatas celulares es inmensamente rica, con reglas y estructuras simples capaces de producir una gran variedad de comportamientos inesperados. Por ejemplo, existen autómatas celulares universales que son capaces de simular el comportamiento de cualquier otro autómata celular o máquina de Turing. Gacs (2001) ha demostrado incluso que existen autómatas celulares universales tolerantes a los fallos, cuya capacidad para simular otros autómatas celulares no se ve obstaculizada por perturbaciones aleatorias, siempre y cuando dichas perturbaciones sean lo suficientemente escasas.