Biografía

Brahmagupta (598-668 d.C.)
El gran matemático y astrónomo indio del siglo VII Brahmagupta escribió algunas obras importantes tanto de matemáticas como de astronomía. Era originario del estado de Rajastán, en el noroeste de la India (a menudo se le conoce como Bhillamalacarya, el maestro de Bhillamala), y más tarde se convirtió en el director del observatorio astronómico de Ujjain, en la India central. La mayoría de sus obras están compuestas en verso elíptico, una práctica común en las matemáticas indias de la época, y por lo tanto tienen algo de anillo poético.
Es probable que las obras de Brahmagupta, especialmente su texto más famoso, el «Brahmasphutasiddhanta», fueran llevadas por el califa abasí del siglo VIII Al-Mansur a su recién fundado centro de aprendizaje en Bagdad, a orillas del Tigris, proporcionando un importante vínculo entre las matemáticas y la astronomía indias y el naciente auge de la ciencia y las matemáticas en el mundo islámico.
En su obra sobre aritmética, Brahmagupta explicó cómo hallar el cubo y la raíz cúbica de un número entero y dio reglas que facilitaban el cálculo de cuadrados y raíces cuadradas. También dio reglas para tratar cinco tipos de combinaciones de fracciones. Dio la suma de los cuadrados de los primeros n números naturales como n(n + 1)(2n + 1)⁄ 6 y la suma de los cubos de los primeros n números naturales como (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Tratar el cero como un número

Reglas de Brahmagupta para tratar el cero y los números negativos
El genio de Brahmagupta, sin embargo, vino en su tratamiento del concepto del (entonces relativamente nuevo) número cero. Aunque a menudo se atribuye también al matemático indio del siglo VII Bhaskara I, su «Brahmasphutasiddhanta» es probablemente el primer texto conocido en el que se trata el cero como un número por derecho propio, en lugar de como un simple dígito marcador de posición, como hacían los babilonios, o como un símbolo de falta de cantidad, como hacían los griegos y los romanos.
Brahmagupta estableció las reglas matemáticas básicas para tratar el cero (1 + 0 = 1; 1 – 0 = 1; y 1 x 0 = 0), aunque su comprensión de la división por cero era incompleta (pensaba que 1 ÷ 0 = 0). Casi 500 años después, en el siglo XII, otro matemático indio, Bhaskara II, demostró que la respuesta debía ser el infinito, no el cero (basándose en que 1 puede dividirse en un número infinito de trozos de tamaño cero), respuesta que se consideró correcta durante siglos. Sin embargo, esta lógica no explica por qué 2 ÷ 0, 7 ÷ 0, etc, deben ser también cero – la opinión moderna es que un número dividido por cero es en realidad «indefinido» (es decir, no tiene sentido).
La visión de Brahmagupta de los números como entidades abstractas, en lugar de sólo para contar y medir, le permitió dar otro enorme salto conceptual que tendría profundas consecuencias para las matemáticas futuras. Anteriormente, la suma 3 – 4, por ejemplo, se consideraba sin sentido o, en el mejor de los casos, simplemente cero. Sin embargo, Brahmagupta se dio cuenta de que podía existir un número negativo, al que denominó «deuda» en contraposición a «propiedad». Explicó las reglas para tratar los números negativos (por ejemplo, un negativo por un negativo es un positivo, un negativo por un positivo es un negativo, etc.).
Además, señaló que las ecuaciones cuadráticas (del tipo x2 + 2 = 11, por ejemplo) podían tener en teoría dos posibles soluciones, una de las cuales podía ser negativa, porque 32 = 9 y -32 = 9. Además de su trabajo sobre las soluciones de las ecuaciones lineales generales y las ecuaciones cuadráticas, Brahmagupta fue aún más lejos al considerar los sistemas de ecuaciones simultáneas (conjunto de ecuaciones que contienen múltiples variables), y la resolución de ecuaciones cuadráticas con dos incógnitas, algo que ni siquiera se consideró en Occidente hasta mil años después, cuando Fermat consideraba problemas similares en 1657.
Teorema de Brahmagupta sobre los cuadriláteros cíclicos
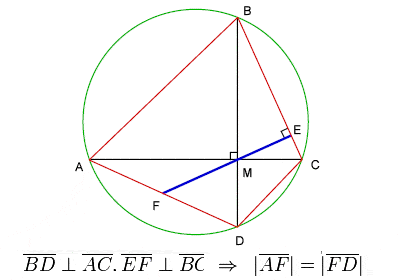
Teorema de Brahmagupta sobre los cuadriláteros cíclicos
Brahmagupta incluso intentó escribir estos conceptos bastante abstractos, utilizando las iniciales de los nombres de los colores para representar incógnitas en sus ecuaciones, uno de los primeros indicios de lo que hoy conocemos como álgebra.
Brahmagupta dedicó una parte sustancial de su obra a la geometría y la trigonometría. Estableció √10 (3,162277) como una buena aproximación práctica para π (3,141593), y dio una fórmula, ahora conocida como Fórmula de Brahmagupta, para el área de un cuadrilátero cíclico, así como un célebre teorema sobre las diagonales de un cuadrilátero cíclico, usualmente referido como Teorema de Brahmagupta.
| << Volver a Matemáticas Indias | Adelante con Madhava >> |