Las coordenadas baricéntricas son triples de números 
correspondientes a masas situadas en los vértices de un triángulo de referencia 
. Estas masas determinan entonces un punto 
, que es el centroide geométrico de las tres masas y se identifica con las coordenadas 
. Los vértices del triángulo vienen dados por 
, 
, y 
. Las coordenadas baricéntricas fueron descubiertas por Möbius en 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).
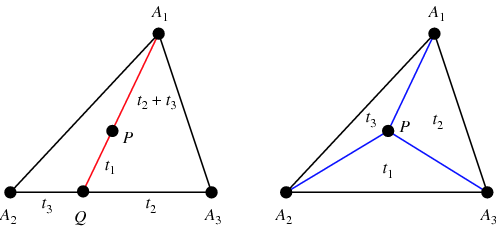
Para hallar las coordenadas baricéntricas de un punto arbitrario 
, hallar 
y 
desde el punto 
en la intersección de la recta 
con el lado 
, y luego determinar 
como la masa en 
que equilibrará una masa 
en 
, haciendo así de 
el centroide (figura izquierda). Además, las áreas de los triángulos 
, 
y 
son proporcionales a las coordenadas baricéntricas 
, 
y 
de 
(figura derecha; Coxeter 1969, p. 217).¡
Las coordenadas baricéntricas son homogéneas, por lo que
 |
(1)
|
para 
.
Las coordenadas baricéntricas normalizadas de forma que se conviertan en las áreas reales de los subtriángulos se denominan coordenadas baricéntricas homogéneas. Las coordenadas baricéntricas normalizadas de modo que
 |
(2)
|
de modo que las coordenadas dan las áreas de los subtriángulos normalizadas por el área del triángulo original se llaman coordenadas areales (Coxeter 1969, p. 218). Las coordenadas baricéntricas y areales pueden proporcionar pruebas particularmente elegantes de teoremas geométricos como el teorema de Routh, el teorema de Ceva y el teorema de Menelao (Coxeter 1969, pp. 219-221).
(No necesariamente homogéneas) las coordenadas baricéntricas para una serie de centros comunes se resumen en la siguiente tabla. En la tabla, 
, 
, y 
son las longitudes de los lados del triángulo y 
es su semiperímetro.
| centro del triángulo | coordenadas baricéntricas |
circuncentro  |
( ,  ,  ) |
excenter  |
 |
excenter  |
 |
excenter  |
 |
| Punto de Gergonne Ge | ( ,  ,  ) |
incentro  |
 |
| Punto Nagel Na |  |
ortocentro  |
( ,  ,  ) |
punto simétrico  |
 |
centroide del triángulo  |
 |
En coordenadas baricéntricas, una recta tiene una ecuación lineal homogénea. En particular, la recta que une los puntos 
y 
tiene ecuación
 |
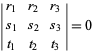(3)
|
(Loney 1962, pp. 39 y 57; Coxeter 1969, p. 219; Bottema 1982). Si los vértices 
de un triángulo 
tienen coordenadas baricéntricas 
, entonces el área del triángulo es
 |
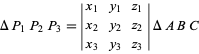(4)
|
(Bottema 1982, Yiu 2000).