Factor de compresibilidad (gases) - Knowino

De Knowino

Esta es una versión revisada de esta página

Saltar a: navegación,búsqueda

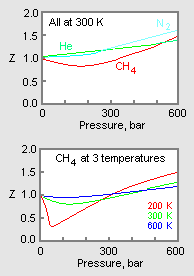
Figura 1: Gráficos de ejemplo de los factores de compresibilidad de los gases

El factor de compresibilidad (Z) es una propiedad termodinámica útil para modificar la ley de los gases ideales y dar cuenta del comportamiento de los gases reales. Es una medida de cuánto se desvían las propiedades termodinámicas de un gas real de las esperadas de un gas ideal. Puede considerarse como la relación entre el volumen real de un gas real y el volumen predicho por el gas ideal a la misma temperatura y presión que el volumen real.

Para un gas ideal, Z siempre tiene un valor de 1. Para los gases reales, el valor puede desviarse positiva o negativamente, dependiendo del efecto de las fuerzas intermoleculares del gas. Cuanto más cerca esté un gas real de su punto crítico o de su punto de saturación, mayores serán las desviaciones del gas respecto al comportamiento ideal.

El gráfico superior de la figura 1 ilustra cómo varía el factor de compresibilidad para diferentes gases a la misma temperatura y presión. El gráfico inferior ilustra cómo varía el factor de compresibilidad de un gas (por ejemplo, el metano) a una presión determinada con la temperatura.

Este artículo trata únicamente del factor de compresibilidad de los gases y no profundiza en la compresibilidad de los líquidos o de las mezclas vapor-líquido.

Contenidos

1 Determinación de los valores de compresibilidad de los gases
- 1.1 Gráficos del factor de compresibilidad generalizado para gases puros
- 1.2 Gráficos del factor de compresibilidad generalizado para mezclas de gases
- 1.3 La ecuación de van der Waals
  - 1.3.1 Versiones modificadas de la ecuación de van der Waals
    - 1.3.1.1 Redlich-Kwong
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
- 1.4 Ecuación de estado virial
- 1.5 Otras ecuaciones de estado
- 1.5.1.1.2.2.2.3.3.3.3.3.4.3.4.4.4.4.5.4.5.4.5.5.5.5.5.5.5.5.5.5.5.5.5.6. Ecuación de estado
- 1.6 Notación para la constante de los gases
2 Referencias

Determinación de los valores de compresibilidad de los gases

La ley de los gases ideales se define como:

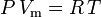
$P\N,V_mathrm{m} = R\,T$

y la ley de los gases ideales corregida por la no idealidad se define es:

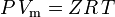
$P\N,V_mathrm{m} = ZR\,T$

donde:
P	= presión
Vm	= volumen molar del gas
Z	= factor de compresibilidad
R	= constante universal de los gases
T	= temperatura

y así:

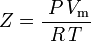
$Z = \frac{;P\,V_mathrm{m}}{R\,T}$

que es la ecuación de estado de los gases reales (EOS) más simple y más utilizada. La principal limitación de esta ecuación de estado es que el factor de compresibilidad del gas, Z, no es una constante, sino que varía de un gas a otro, así como con la temperatura y la presión del gas considerado. Debe determinarse experimentalmente.

Cuando se dispone de datos experimentales para gases específicos, esos datos pueden utilizarse para producir gráficos (como el de la figura 1) de Z frente a la presión a una temperatura constante o de Z frente a la presión para varias temperaturas para esos gases específicos. Estos gráficos son útiles para obtener fácilmente valores interpolados de Z entre los valores determinados experimentalmente.

El factor de compresibilidad, como se mencionó anteriormente, también puede expresarse como:

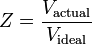
$Z = \frac{V_\mathrm{actual}{V_\mathrm{ideal}$

Hay tres regímenes que afectan al factor de compresibilidad:

el valor de Z tiende a 1 a medida que la presión del gas se acerca a 0, donde todos los gases tienden al comportamiento ideal
el valor de Z es menor que 1 a presiones intermedias porque las fuerzas intermoleculares de atracción hacen que los volúmenes reales sean menores que los valores ideales
el valor de Z es mayor que 1 y finalmente tiende al infinito a altas presiones porque las fuerzas intermoleculares de repulsión hacen que los volúmenes reales sean mayores que los valores ideales

Gráficas del factor de compresibilidad generalizado para gases puros

La relación única entre el factor de compresibilidad y la temperatura reducida, Tr, y la presión reducida, Pr, fue reconocida por primera vez por van der Waals en 1873 y se conoce como el principio de dos parámetros de los estados correspondientes. El principio de los estados correspondientes expresa la generalización de que las propiedades de un gas que dependen de las fuerzas intermoleculares están relacionadas con las propiedades críticas del gas de forma universal. Esto proporciona una base muy importante para desarrollar correlaciones de las propiedades moleculares.

En cuanto a la compresibilidad de los gases, el principio de los estados correspondientes indica que cualquier gas puro a la misma temperatura reducida, Tr, y a la misma presión reducida, Pr, debería tener el mismo factor de compresibilidad.

La temperatura y la presión reducidas se definen como:

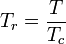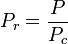
$T_r = \frac{T}{T_c}$ y $P_r = \frac{P}{P_c}$

Tc y Pc se conocen como la temperatura crítica y la presión crítica de un gas. Son características de cada gas específico siendo Tc la temperatura por encima de la cual no es posible licuar un gas determinado y Pc es la presión mínima necesaria para licuar un gas determinado a su temperatura crítica. Juntos definen el punto crítico de un fluido por encima del cual no existen las fases líquida y gaseosa de un determinado fluido.

Los datos de presión-volumen-temperatura (PVT) de los gases reales varían de un gas puro a otro. Sin embargo, cuando los factores de compresibilidad de varios gases de un solo componente se grafican frente a la presión junto con las isotermas de temperatura (como se muestra para el metano en el gráfico inferior de la Figura 1), muchos de los gráficos exhiben formas de isoterma similares.

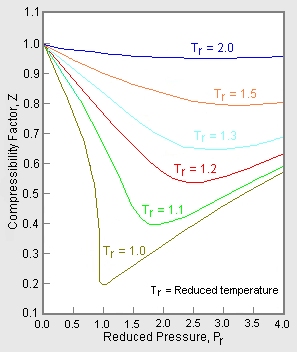
Figura 2: Ejemplo de gráfico de factor de compresibilidad generalizado

Para obtener un gráfico generalizado que pueda utilizarse para muchos gases diferentes, la presión y la temperatura reducidas, Pr y Tr, se utilizan para normalizar los datos del factor de compresibilidad. La figura 2 es un ejemplo de un gráfico de factor de compresibilidad generalizado derivado de cientos de puntos de datos experimentales P-V-T de 10 gases puros, a saber, metano, etano, etileno, propano, n-butano, i-pentano, n-hexano, nitrógeno, dióxido de carbono y vapor.

Existen gráficos de factor de compresibilidad generalizados más detallados basados en hasta 25 o más gases puros diferentes, como los gráficos de Nelson-Obert. Se dice que estos gráficos tienen una precisión del 1-2 por ciento para valores de Z superiores a 0,6 y del 4-6 por ciento para valores de Z de 0,3-0,6.

Los gráficos del factor de compresibilidad generalizado pueden tener un error considerable en el caso de los gases fuertemente polares, que son gases cuyos centros de carga positiva y negativa no coinciden. En estos casos, la estimación de Z puede tener un error de hasta el 15-20 por ciento.

Los gases cuánticos hidrógeno, helio y neón no se ajustan al comportamiento de los estados correspondientes y la presión y la temperatura reducidas para esos tres gases deben redefinirse de la siguiente manera para mejorar la precisión de la predicción de sus factores de compresibilidad cuando se utilizan los gráficos generalizados:

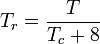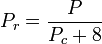
$T_r = \frac{T}{T_c + 8}$ y $P_r = \frac{P}{P_c + 8}$

donde las temperaturas están en grados Kelvin y las presiones en atmósferas.

Gráficos del factor de compresibilidad generalizado para mezclas de gases

Los gráficos del factor de compresibilidad generalizado para gases puros (como los ejemplificados en la figura 2 o los gráficos de Nelson-Obert también pueden utilizarse para mezclas de gases utilizando la regla de Kay propuesta por W. B. Kay en 1936. Esa regla predice el comportamiento P-V-T de una mezcla de gases determinando el factor de compresibilidad para una mezcla de gases a la temperatura reducida y a la presión reducida definida en términos de la temperatura pseudocrítica, Tpc y la presión pseudocrítica, Ppc que se definen como:

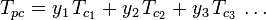
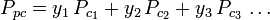
$T_{pc} = y_1,T_{c_1} + y_2,T_{c_2} + y_3,T_{c_3},\dots$ $P_{pc} = y_1,P_{c_1} + y_2,P_{c_2} + y_3,P_{c_3}\Npuntos$

donde:
Tpc	= la temperatura pseudocrítica de la mezcla de gases
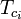$T_{c_i}$	= la temperatura crítica de un componente de la mezcla de gases
Ppc	= la presión pseudocrítica presión de la mezcla de gases
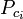$P_{c_i}$	= la temperatura crítica de un componente del gas
yi	= la fracción molar (o de volumen) de un componente del gas

La temperatura pseudorreducida, Tpr, y la presión pseudoreducida, Ppr, para usar con las gráficas del factor de compresibilidad generalizado para gases puros son entonces:

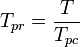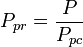
$T_{pr} = \frac{T}{T_{pc}}$ y $P_{pr} = \frac{P}{P_{pc}}$

Un gráfico del factor de compresibilidad para el gas natural (que es una mezcla de hidrocarburos y otros gases) utilizando temperaturas y presiones pseudoreducidas está disponible en Internet.

La ecuación de van der Waals

La ecuación de van der Waals fue desarrollada en 1873 y puede ser expresada como:

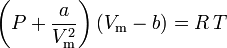
$left(P + \frac{a}{V_\mathrm{}^2}right)\left(V_\mathrm{} - b\right) = R\,T$

donde:

a es una medida de la fuerza de atracción entre las moléculas de gas b da cuenta del volumen ocupado por las moléculas de gas, lo que disminuye el volumen abierto disponible

La ecuación de van der Waals puede reordenarse como:

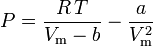
$P = \frac{R,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

y el factor de compresibilidad puede escribirse como:

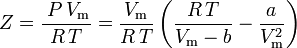
$Z = \frac{;P\N,V_mathrm{m}{R\N,T} = \frac{V_mathrm{m}{R\N,T}left(\frac{R,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}^2}right)$

y ahora tenemos una ecuación para determinar Z utilizando los parámetros de van der Waals a y b:

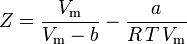
$Z = \frac{V_\mathrm{m}}{V_\mathrm{m}} - \frac{a}{R\,T\,V_\mathrm{m}}$

Aunque a y b se denominan «las constantes de Van der Waals», no son realmente constantes porque varían de un gas a otro; sin embargo, son independientes de P, V y T. En otras palabras, son constantes para el gas considerado. Dadas la temperatura y la presión críticas para un gas específico, a y b pueden obtenerse para ese gas específico a partir de estas ecuaciones:

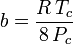
$a = \frac{27\, R^2\, T_c^2}{64\, P_c}$ y $b = \frac{R\, T_c}{8\, P_c}$

Por ejemplo, la presión crítica del etano es 4.884 MPa y la temperatura crítica es de 305,43 K (32,3˚C). Utilizando la constante universal de los gases, R, de 8,3145 Pa m3 K-1 mol-1, las ecuaciones anteriores dan como resultado a = 0,557 m6 Pa mol-2 y b = 6,500×10-5 m3 mol-1.

Los valores tabulados de a y b para varios gases están disponibles en estas referencias así como en muchas otras fuentes de la literatura técnica.

Versiones modificadas de la ecuación de van der Waals

Determinar los factores de compresibilidad mediante el uso de la ecuación de estado de van der Waals es una mejora sobre el uso de las tablas de compresibilidad generalizada. Sin embargo, existen versiones modificadas de la ecuación de estado de van der Waals que proporcionan una mejora aún mayor. Quizás las ecuaciones de estado más utilizadas por los ingenieros que trabajan en el refinado de petróleo, la producción petroquímica, el procesamiento de gas natural, la destilación criogénica y otras industrias relacionadas son: la ecuación de Redlich-Kwong desarrollada en 1949, la ecuación de Soave-Redlich-Kwong desarrollada en 1972 y la ecuación de Peng-Robinson desarrollada en 1976. Estas tres ecuaciones son esencialmente versiones modificadas de la ecuación de van der Waals. Las ecuaciones comparativas son:

Redlich-Kwong

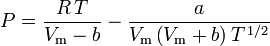
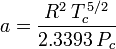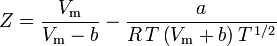
$P = \frac{R,T}{V_\mathrm{m}} - b} - \frac{a}{V_\mathrm{m}{left(V_\mathrm {m} + b\right)T^{,1/2}$ $a = \frac{R^2, T_c^{,5/2}{2.3393\, P_c}$ y $b = \frac{R\, T_c}{11.5420, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{,1/2}$

Soave-Redlich-Kwong

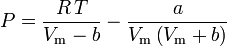
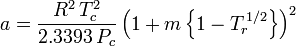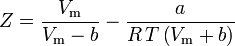
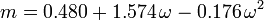
$P = \frac{R,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}{izquierda(V_mathrm{m} + b\ derecha)}$ $a = \frac{R^2,T_c^2}{2.3393,P_c}, \Big(1 + m\, \Big{1 - T_r^,1/2} \Big)^2$ y $b = \frac{R, T_c}{11.5420\, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)}$ $m = 0.480 + 1,574\, \omega - 0,176\, \omega^2$

El factor acéntrico, ω, utilizado como parámetro en las ecuaciones de Soave-Redlich-Kwong y Peng-Robinson fue introducido por primera vez por Pitzer et al en 1955. Puede expresarse como:

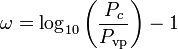
$\a = \log_{10} \left(\frac{P_c}{P_\mathrm{vp}}right) - 1$

donde Pvp es la presión de vapor saturada del gas a una temperatura de 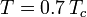$T = 0,7\, T_c$ .

Peng-Robinson

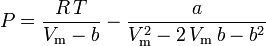
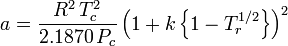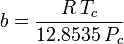
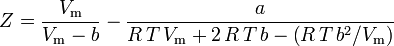
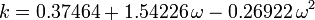
$P = \frac{R,T}{V_\mathrm{m}} - b} - \frac{a}{V_\mathrm{m}^2 - 2\\ V_\mathrm{m}, b - b^2}$ $a = \frac{R^2,T_c^2}{21870,P_c}, \Big(1 + k\\, \Big{1 - T_r^{1/2} \Big)^2$ y $b = \frac{R,T_c}{12,8535\, P_c}$ $Z = \frac{V_mathrm{m}}{V_mathrm{m} - b} - \frac{a}{R,T\,V_mathrm{m} + 2\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)}$ $k = 0,37464 + 1,54226\, \omega - 0,26922\, \omega^2$

Ecuación de estado virial

La ecuación de estado más fundamental , en cuanto a que tiene el fundamento teórico más sólido, es la ecuación de estado virial:

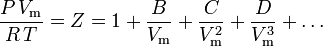
${frac{P,V_mathrm{m}{R\a,T} = Z = 1 + \frac{B}{V_mathrm{m} + \frac{C}{V_mathrm{m}^2} + \frac{D} {V_\mathrm{m}^3} + \dots$

Fue propuesto por primera vez sobre una base empírica por Thiesen en 1885 y desarrollado en 1901 por Kamerlingh-Onnes. Ornstein dedujo por primera vez una expresión estadístico-mecánica para B en su tesis doctoral. Posteriormente, H.D. Ursell volvió a desarrollar la ecuación en 1927 sobre una base teórica derivada de un análisis estadístico-mecánico (cluster) de las fuerzas intermoleculares.

Los parámetros B, C y D se denominan segundo, tercer y cuarto coeficientes viriales, respectivamente. Los coeficientes no son constantes, ya que varían de un gas a otro, así como la temperatura del gas considerado. A veces se escriben como B(T), C(T) y D(T) para indicar que son funciones de la temperatura. El valor numérico de los coeficientes debe determinarse experimentalmente.

El segundo coeficiente virial proporciona la mayor parte de la corrección por el comportamiento no ideal de un gas. Por esa razón, la ecuación virial a veces se trunca después del término que contiene el segundo coeficiente. Sin embargo, cuando se dispone del tercer coeficiente, la ecuación se suele truncar después del término que contiene el tercer coeficiente. El cuarto coeficiente rara vez está disponible.

Una extensa compilación de coeficientes viriales para gases puros y mezclas de gases se preparó a partir de la base de datos de coeficientes viriales del Centro de Investigación de Termodinámica, anteriormente en la Universidad de Texas A&M, College Station, Texas, y que ahora se encuentra en el Instituto Nacional de Normas y Tecnología (NIST), Boulder, Colorado. La última versión de esa compilación se publicó en 2003. El NIST también ofrece para su compra un programa de software, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), que incluye los coeficientes viriales segundo y tercero, así como una serie de otras propiedades termodinámicas.

Otras ecuaciones de estado

Hay una serie de otras ecuaciones de estado para predecir el comportamiento de los gases reales. Quizás, las más conocidas son la ecuación Beattie-Bridgeman desarrollada en 1929 y la ecuación Benedict-Rubin-Webb desarrollada en 1940. En general, son más complejas que las ecuaciones discutidas anteriormente.

Notación para la constante de los gases

La constante de los gases utilizada en este artículo es la constante universal de los gases, R, que se aplica a cualquier gas. También existe una constante específica de los gases, que se puede denotar como Rs, y se define como Rs = R / M donde M es el peso molecular.

Desgraciadamente, muchos autores de la literatura técnica utilizan a veces R como la constante específica de los gases sin denotarla como tal o indicando que es la constante específica de los gases. Esto puede llevar y lleva a confusión.

1,0 1,1 1,2 1,3 1,4 McQuarrie, Donald A. y Simon, John D. (1999). Molecular Thermodynamics. University Science Books. ISBN 1-891389-05-X.
2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal y Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, 2nd Edition. McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Introduction to Chemical Engineering Thermodynamics, Seventh Edition. McGraw Hill. ISBN 0-07-310445-0.
4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Chemical Engineering Thermodynamics. Universities Press (India). ISBN 81-7371-048-1.
5.0 5.1 Gas Laws (Lecture by Professor M.J. Mombourquette at Queens University, Canada)
Hong Wei Xiang (2005). El principio de los estados correspondientes y su práctica: Thermodynamic, Transport and Surface Properties of Fluids. Elsevier. ISBN 0-444-52062-7.
IUPAC Goldbook
Gouq-Jen Su (1946). «Ley modificada de los estados correspondientes». Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.
9.0 9.1 Equations of State (Professor Lyes Kadem, Concordia University, Canada)
10.0 10.1 Equations of State (Lecture material used by Professor Sanford Klein at the University of Wisconsin-Madison, U.S.)
Richard W. Miller (1996). Flow Measurement Engineering Handbook, 3ª edición. McGraw-Hill. ISBN 0-07-042366-0. (Véase la figura G-1 en la página G.145)
Kai-Fui Vincent Wong (2000). Thermodynamics for Engineers, 1st Edition. CRC Press. ISBN 0-8493-0232-3. (Véase la figura A-2, página 278}
Tablas de compresibilidad generalizada de Nelson-Obert (Tablas disponibles en Internet, en la página web de la Universidad Estatal de San Diego, EE.UU.)
W.B.Kay (1936). «Gases y vapores a alta temperatura y presión – Densidad del hidrocarburo». Ingeniería Industrial & Química 28:1014. ISSN 0096-4484.
Yunus A. Çengal y Michael A. Bowes (2005). Termodinámica: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
Real Gases (Material de lectura utilizado por el profesor R.M. Price en la Christian Brothers University, EE.UU.)
Properties of Natural Gases (Profesor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
Robert C. Weast (Editor) (1975). Handbook of Chemistry and Physics, 56th Edition. CRC Press. ISBN 0-87819-455-X.
19.0 19.1 19.2 Capítulo 3: Ecuaciones de estado (páginas 6-8 de 65 páginas pdf) (Parte de la tesis doctoral de Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)
20.0 20.1 20.2 Jean Vidal (2003). Thermodynamics: Aplicaciones en Ingeniería Química y en la Industria del Petróleo. Ediciones Technip. ISBN 2-7108-0800-5.
Zakia Nasri y Housam Binous (2007). «Applications of the Soave-Redlich-Kwong Equation of State Using Mathematica». Journal of Chemical Engineering of Japan 40 (6): 534-538. Recuperado de aquí.
K.S. Pitzer et al (1955). «Las propiedades volumétricas y termodinámicas de los fluidos». Journal of the American Chemical Society 77: 3427-3440.
Francis S. Manning y Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
Definición del factor acéntrico (Physical Property Sources Index, PPSI, del Instituto Federal Suizo de Tecnología de Zurich)
Max F. Thiesen (1885). «Investigaciones de la ecuación de estado». Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901). «Expresión de la ecuación de estado de gases y líquidos por medio de series». Commun. Phys. Lab. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Aplicación de la mecánica estadística de Gibbs en problemas teóricos moleculares), Leiden
H. D. Ursell (1927). «La evaluación de la integral de fase de Gibbs para gases imperfectos» (23): 685.
J.D. Dymond y R.C. Wilhoit (Autores), K.N. Marsch y M. Fenkel (Editores) (2003). Virial Coefficients of Pure gases and Mixtures, 1st Edition. Springer. ISBN 3-540-44340-1.
Base de datos de referencia estándar del NIST 23
J.A. Beattie y O.C. Bridgeman (1929). «Una nueva ecuación de estado para los fluidos». Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb y L.C. Rubin (1940). «Una ecuación empírica para las propiedades termodinámicas de los hidrocarburos ligeros y sus mezclas». J. Chem. Phys. 8: 334-335.

Parte del contenido de esta página puede haber aparecido previamente en Citizendium.

Recuperado de «http://knowino.org/wiki/Compressibility_factor_(gases)»

Categoría: Física