Una matriz de confusión es una tabla que se utiliza a menudo para describir el rendimiento de un modelo de clasificación (o «clasificador») en un conjunto de datos de prueba para los que se conocen los valores verdaderos. La matriz de confusión en sí misma es relativamente sencilla de entender, pero la terminología relacionada puede ser confusa.
Quería crear una «guía de referencia rápida» para la terminología de las matrices de confusión porque no pude encontrar un recurso existente que se ajustara a mis requisitos: presentación compacta, utilizando números en lugar de variables arbitrarias, y explicada tanto en términos de fórmulas como de frases.
Empecemos con un ejemplo de matriz de confusión para un clasificador binario (aunque se puede extender fácilmente al caso de más de dos clases):
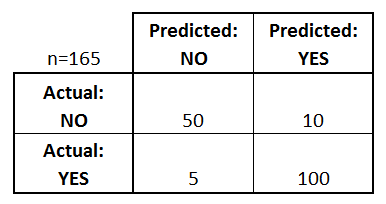
¿Qué podemos aprender de esta matriz?
- Hay dos posibles clases predichas: «sí» y «no». Si estuviéramos prediciendo la presencia de una enfermedad, por ejemplo, «sí» significaría que tienen la enfermedad, y «no» significaría que no tienen la enfermedad.
- El clasificador hizo un total de 165 predicciones (por ejemplo, 165 pacientes se sometieron a la prueba de la presencia de esa enfermedad).
- De esos 165 casos, el clasificador predijo «sí» 110 veces, y «no» 55 veces.
- En realidad, 105 pacientes de la muestra tienen la enfermedad, y 60 pacientes no.
Definamos ahora los términos más básicos, que son números enteros (no tasas):
- verdaderos positivos (TP): Son los casos en los que predijimos que sí (tienen la enfermedad), y la tienen.
- verdaderos negativos (TN): Predijimos que no, y no tienen la enfermedad.
- falsos positivos (FP): Predijimos que sí, pero en realidad no tienen la enfermedad. (También conocido como «error de tipo I»)
- falsos negativos (FN): Predijimos que no, pero en realidad tienen la enfermedad. (También conocido como «error de tipo II»)
He añadido estos términos a la matriz de confusión, y también he añadido los totales de las filas y las columnas:
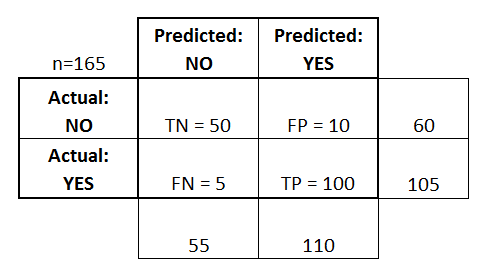
Esta es una lista de índices que suelen calcularse a partir de una matriz de confusión para un clasificador binario:
- Precisión: En general, ¿con qué frecuencia es correcto el clasificador?
- (TP+TN)/total = (100+50)/165 = 0,91
- Tasa de clasificación errónea: En general, ¿con qué frecuencia se equivoca?
- (FP+FN)/total = (10+5)/165 = 0,09
- equivalente a 1 menos la Precisión
- también conocida como «Tasa de error»
- Tasa de verdaderos positivos: Cuando es realmente sí, ¿con qué frecuencia predice el sí?
- TP/sí real = 100/105 = 0,95
- también conocida como «Sensibilidad» o «Recall»
- Tasa de falsos positivos: Cuando es realmente un no, ¿con qué frecuencia predice un sí?
- FP/no real = 10/60 = 0,17
- Tasa de verdaderos negativos: Cuando realmente es no, ¿con qué frecuencia predice el no?
- TN/no real = 50/60 = 0,83
- equivalente a 1 menos la tasa de falsos positivos
- también conocida como «Especificidad»
- Precisión: Cuando predice un sí, ¿con qué frecuencia es correcto?
- TP/previsión de sí = 100/110 = 0,91
- Prevalencia: ¿Con qué frecuencia se produce realmente la condición de sí en nuestra muestra?
- Sí real/total = 105/165 = 0,64
También vale la pena mencionar un par de términos más:
- Tasa de error nulo: Es la frecuencia con la que te equivocarías si siempre predijeras la clase mayoritaria. (En nuestro ejemplo, la tasa de error nulo sería 60/165=0,36 porque si siempre predijeras que sí, sólo te equivocarías en los 60 casos de «no»). Esta puede ser una métrica de referencia útil para comparar su clasificador. Sin embargo, el mejor clasificador para una aplicación concreta tendrá a veces una tasa de error más alta que la tasa de error nula, como demuestra la Paradoja de la Precisión.
- Kappa de Cohen: Es esencialmente una medida de lo bien que funcionó el clasificador en comparación con lo bien que habría funcionado simplemente por azar. En otras palabras, un modelo tendrá una puntuación Kappa alta si hay una gran diferencia entre la precisión y la tasa de error nula. (Más detalles sobre el Kappa de Cohen.)
- Puntuación F: Es una media ponderada de la tasa de verdaderos positivos (recall) y la precisión. (Más detalles sobre la puntuación F.)
- Curva ROC: Es un gráfico comúnmente utilizado que resume el rendimiento de un clasificador sobre todos los umbrales posibles. Se genera trazando la Tasa de Verdaderos Positivos (eje y) contra la Tasa de Falsos Positivos (eje x) a medida que se varía el umbral para asignar las observaciones a una clase determinada. (Más detalles sobre las curvas ROC.)
Y, por último, para los que proceden del mundo de la estadística bayesiana, he aquí un rápido resumen de estos términos de Applied Predictive Modeling:
En relación con la estadística bayesiana, la sensibilidad y la especificidad son las probabilidades condicionales, la prevalencia es el previo, y los valores positivos/negativos predichos son las probabilidades posteriores.
¿Quieres saber más?
En mi nuevo vídeo de 35 minutos, Making sense of the confusion matrix, explico estos conceptos con más profundidad y cubro temas más avanzados:
- Cómo calcular la precisión y el recuerdo para problemas multiclase
- Cómo analizar una matriz de confusión de 10 clases
- Cómo elegir la métrica de evaluación adecuada para su problema
- Por qué la precisión es a menudo una métrica engañosa
¡Hágame saber si tiene alguna pregunta!