Objetivo de aprendizaje
1. Convertir de una unidad a otra del mismo tipo.
En la sección 2.2 «Expresión de unidades», mostramos algunos ejemplos de cómo sustituir las unidades iniciales por otras del mismo tipo para obtener un valor numérico más fácil de comprender. En esta sección, formalizaremos el proceso.
Considere un ejemplo sencillo: ¿cuántos pies hay en 4 yardas? La mayoría de la gente responderá casi automáticamente que hay 12 pies en 4 yardas. ¿Cómo han llegado a esta determinación? Bueno, si hay 3 pies en 1 yarda y hay 4 yardas, entonces hay 4 × 3 = 12 pies en 4 yardas.
Esto es correcto, por supuesto, pero es informal. Formalicémoslo de manera que pueda aplicarse de forma más general. Sabemos que 1 yarda (yd) es igual a 3 pies (ft):
1 yd = 3 ft
En matemáticas, esta expresión se llama igualdad. Las reglas del álgebra dicen que se puede cambiar (es decir, multiplicar o dividir o sumar o restar) la igualdad (siempre que no se divida por cero) y la nueva expresión seguirá siendo una igualdad. Por ejemplo, si dividimos ambos lados por 2, obtenemos
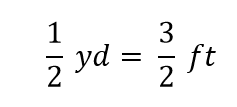
Vemos que la mitad de una yarda es igual a 3/2, o un pie y medio, algo que también sabemos que es cierto, así que la ecuación anterior sigue siendo una igualdad. Volviendo a la igualdad original, supongamos que dividimos ambos lados de la ecuación por 1 yarda (número y unidad):
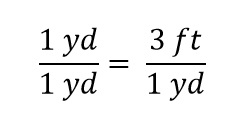
La expresión sigue siendo una igualdad, por las reglas del álgebra. La fracción de la izquierda es igual a 1. Tiene la misma cantidad en el numerador y en el denominador, por lo que debe ser igual a 1. Las cantidades en el numerador y el denominador se cancelan, tanto el número como la unidad:
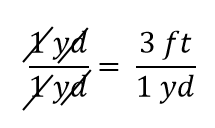
Cuando todo se cancela en una fracción, la fracción se reduce a 1:
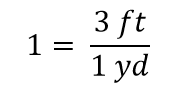
Tenemos una expresión, 3 ft1 yd, que es igual a 1. Esta es una forma extraña de escribir 1, pero tiene sentido: 3 pies equivalen a 1 yd, por lo que las cantidades en el numerador y el denominador son la misma cantidad, sólo que expresada con diferentes unidades. La expresión 3 ft1 yd se llama factor de conversión, y se utiliza para cambiar formalmente la unidad de una cantidad en otra unidad. (El proceso de convertir unidades de esta manera formal se llama a veces análisis dimensional o método de la etiqueta de factores.)
Para ver cómo ocurre esto, empecemos con la cantidad original:
4 yd
Ahora multipliquemos esta cantidad por 1. Cuando se multiplica cualquier cosa por 1, no se cambia el valor de la cantidad. En lugar de multiplicar por 1, escribamos 1 como 3 pies1 yd:
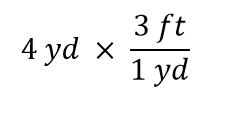
El término 4 yd puede pensarse como 4 yd/1; es decir, puede pensarse como una fracción con 1 en el denominador. Esencialmente estamos multiplicando fracciones. Si la misma cosa aparece en el numerador y el denominador de una fracción, se cancelan. En este caso, lo que se cancela es la unidad yarda:
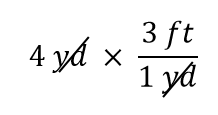
Eso es todo lo que podemos cancelar. Ahora, multiplica y divide todos los números para obtener la respuesta final: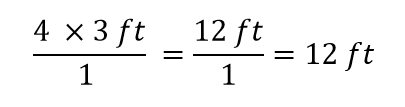
De nuevo, obtenemos una respuesta de 12 pies, como hicimos originalmente. Pero en este caso, utilizamos un procedimiento más formal que es aplicable a una variedad de problemas.
¿Cuántos milímetros hay en 14,66 m? Para responder a esto, necesitamos construir un factor de conversión entre milímetros y metros y aplicarlo correctamente a la cantidad original. Empezamos con la definición de milímetro, que es
1 mm = 1/1.000 m
El 1/1.000 es lo que significa el prefijo milli-. La mayoría de la gente se siente más cómoda trabajando sin fracciones, así que reescribiremos esta ecuación llevando el 1.000 al numerador del otro lado de la ecuación:
1.000 mm = 1 m
Ahora construimos un factor de conversión dividiendo una cantidad en ambos lados. Pero ahora surge una pregunta: ¿entre qué cantidad dividimos? Resulta que tenemos dos opciones, y las dos opciones nos darán factores de conversión diferentes, ambos iguales a 1:
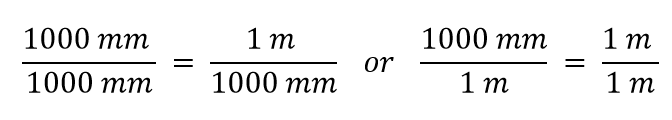
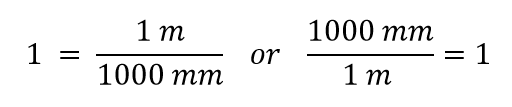
¿Qué factor de conversión utilizamos? La respuesta se basa en la unidad de la que queremos deshacernos en nuestra cantidad inicial. La unidad original de nuestra cantidad es el metro, que queremos convertir en milímetros. Como se supone que la unidad original está en el numerador, para deshacernos de ella, queremos que la unidad de metros esté en el denominador; entonces se cancelarán. Por lo tanto, utilizaremos el segundo factor de conversión. Cancelando las unidades y realizando las matemáticas, obtenemos
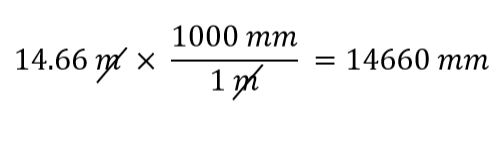
Nota cómo la m se cancela, dejando el mm, que es la unidad de interés.
La habilidad para construir y aplicar factores de conversión adecuados es una técnica matemática muy poderosa en química. Necesita dominar esta técnica si quiere tener éxito en este y en futuros cursos.
Ejemplo 7
- Convierta 35,9 kL a litros.
- Convierta 555 nm a metros.
Solución
-
Utilizaremos el hecho de que 1 kL = 1.000 L. De los dos factores de conversión que se pueden definir, el que funcionará es 1.000 L/1 kL. Aplicando este factor de conversión, obtenemos
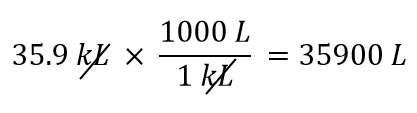
-
Utilizaremos el hecho de que 1 nm = 1/1.000.000.000 m, que reescribiremos como 1.000.000.000 nm = 1 m, o 109 nm = 1 m. De los dos factores de conversión posibles, el apropiado tiene la unidad nm en el denominador: 1 m/109 nm. Aplicando este factor de conversión, obtenemos
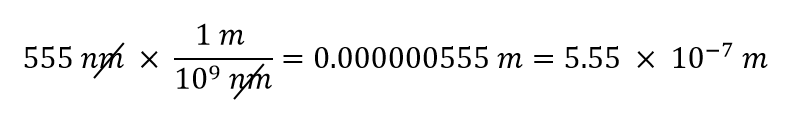
En el último paso, expresamos la respuesta en notación científica.
Ponte a prueba
- Convierte 67.08 μL a litros.
- Convierte 56,8 m a kilómetros.
Respuestas
- 6,708 × 10-5 L
- 5,68 × 10-2 km
¿Y si tenemos una unidad derivada que es el producto de más de una unidad, como el m2? Supongamos que queremos convertir metros cuadrados en centímetros cuadrados. La clave es recordar que m2 significa m × m, lo que significa que tenemos dos unidades de metros en nuestra unidad derivada. Eso significa que tenemos que incluir dos factores de conversión, uno para cada unidad. Por ejemplo, para convertir 17,6 m2 a centímetros cuadrados, realizamos la conversión de la siguiente manera:
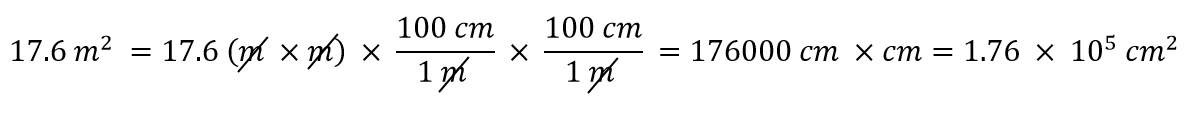
Ejemplo 8
¿Cuántos centímetros cúbicos hay en 0.883 m3?
Solución
Con un exponente de 3, tenemos tres unidades de longitud, por lo que por extensión necesitamos utilizar tres factores de conversión entre metros y centímetros. Así, tenemos
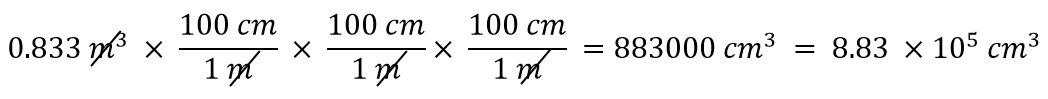
Debes demostrarte a ti mismo que, efectivamente, las tres unidades de metro se cancelan.
Ponte a prueba
¿Cuántos milímetros cúbicos hay en 0,0923 m3?
Respuesta
9,23 × 107 mm3
Supón que la unidad que quieres convertir está en el denominador de una unidad derivada; ¿entonces qué? Entonces, en el factor de conversión, la unidad que quieres eliminar debe estar en el numerador. Esto se cancelará con la unidad original en el denominador e introducirá una nueva unidad en el denominador. El siguiente ejemplo ilustra esta situación.
Ejemplo 9
Convertir 88,4 m/min a metros/segundo.
Solución
Queremos cambiar la unidad en el denominador de minutos a segundos. Como hay 60 segundos en 1 minuto (60 s = 1 min), construimos un factor de conversión para que la unidad que queremos eliminar, los minutos, esté en el numerador: 1 min/60 s. Aplica y realiza los cálculos:
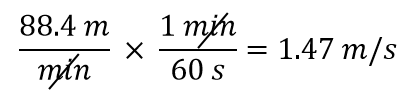
Nota cómo el 88,4 va automáticamente en el numerador. Eso es porque se puede pensar que cualquier número está en el numerador de una fracción dividida por 1.
Ponte a prueba
Convierte 0,203 m/min a metros/segundo.
Respuesta
0.00338 m/s o 3,38 × 10-3 m/s
Figura 2.8 ¿Qué tan rápido es?

Fuente: «Grapevine snail «by Jürgen Schoneris licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.