Son procesos de aprendizaje estocástico que tienen estructura recurrente y son la base de las primeras técnicas de optimización utilizadas en las RNA. La máquina de Boltzmann fue inventada por Geoffrey Hinton y Terry Sejnowski en 1985. Se puede observar más claridad en las palabras de Hinton sobre la Máquina de Boltzmann.
«Una característica sorprendente de esta red es que sólo utiliza la información disponible localmente. El cambio de peso depende sólo del comportamiento de las dos unidades que conecta, aunque el cambio optimiza una medida global» – Ackley, Hinton 1985.
Algunos puntos importantes sobre la Máquina de Boltzmann –
-
Utilizan una estructura recurrente.
-
Están formadas por neuronas estocásticas, que tienen uno de los dos estados posibles, 1 o 0.
-
Algunas de las neuronas son adaptativas (estado libre) y otras están sujetas (estado congelado).
-
Si aplicamos el recocido simulado sobre la red discreta de Hopfield, entonces se convertiría en la Máquina de Boltzmann.
Objetivo de la Máquina de Boltzmann
El objetivo principal de la Máquina de Boltzmann es optimizar la solución de un problema. Es el trabajo de la Máquina de Boltzmann para optimizar los pesos y la cantidad relacionada con ese problema en particular.
Arquitectura
El siguiente diagrama muestra la arquitectura de la máquina de Boltzmann. Está claro en el diagrama, que es una matriz bidimensional de unidades. Aquí, los pesos de las interconexiones entre unidades son -p donde p > 0. Los pesos de las autoconexiones vienen dados por b donde b > 0.
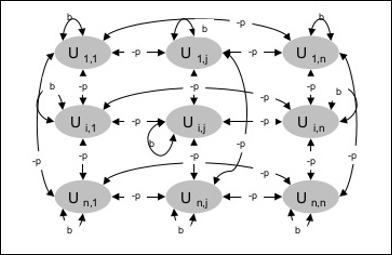
Algoritmo de entrenamiento
Como sabemos que las máquinas de Boltzmann tienen pesos fijos, por tanto no habrá algoritmo de entrenamiento ya que no necesitamos actualizar los pesos de la red. Sin embargo, para probar la red tenemos que establecer los pesos así como encontrar la función de consenso (CF).
La máquina de Boltzmann tiene un conjunto de unidades Ui y Uj y tiene conexiones bidireccionales en ellas.
-
Consideramos el peso fijo digamos wij.
-
wij ≠ 0 si Ui y Uj están conectadas.
-
También existe una simetría en la interconexión ponderada, es decir.e. wij = wji.
-
También existe wii, es decir, existiría la autoconexión entre unidades.
-
Para cualquier unidad Ui, su estado ui sería 1 o 0.
El objetivo principal de la Máquina de Boltzmann es maximizar la Función de Consenso (CF) que puede venir dada por la siguiente relación
$$CF:=:\displaystyle\sum_limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
Ahora, cuando el estado cambia de 1 a 0 o de 0 a 1, entonces el cambio en el consenso puede ser dado por la siguiente relación –
$$Delta CF\:=:(1\:-\:2u_{i})(w_{ij}\\\\N-desde la suma de los límites_{j\neq i} u_{i} w_{ij})$$
Aquí ui es el estado actual de Ui.
La variación del coeficiente (1 – 2ui) viene dada por la siguiente relación –
$$(1\:-\:2u_{i})\:=\Nin{casos}+1, & U_{i}\Nesoff\\\\1, & U_{i}:is:currently:on\end{cases}$$
Generalmente, la unidad Ui no cambia su estado, pero si lo hace entonces la información estaría residiendo localmente en la unidad. Con ese cambio, también se produciría un aumento del consenso de la red.
La probabilidad de que la red acepte el cambio de estado de la unidad viene dada por la siguiente relación –
$$AF(i,T)\N=:\Nfrac{1}{1\:+\:exp}$
Aquí, T es el parámetro de control. Disminuirá a medida que CF alcance el valor máximo.
Algoritmo de prueba
Paso 1 – Inicializar lo siguiente para comenzar el entrenamiento –
- Pesos que representan la restricción del problema
- Parámetro de control T
Paso 2 – Continuar con los pasos 3-8, cuando la condición de parada no es verdadera.
Paso 3 – Realizar los pasos 4-7.
Paso 4 – Suponer que uno de los estados ha cambiado el peso y elegir los enteros I, J como valores aleatorios entre 1 y n.
Paso 5 – Calcule el cambio en el consenso de la siguiente manera –
$$\Delta CF:=\:(1\:-\2u_{i})(w_{ij}\:+\\N-:\displaystyle\\\\Nsuma de límites_{j\neq i} u_{i} w_{ij})$$
Paso 6 – Calcular la probabilidad de que esta red acepte el cambio de estado
$AF(i,T)\N-:=\:\frac{1}{1\:+\:exp}$
Paso 7 – Aceptar o rechazar este cambio de la siguiente manera –
Caso I – si R < AF, aceptar el cambio.
Caso II – si R ≥ AF, rechazar el cambio.
Aquí, R es el número aleatorio entre 0 y 1.
Paso 8 – Reducir el parámetro de control (temperatura) de la siguiente manera –
T(nuevo) = 0.95T(old)
Paso 9 – Probar las condiciones de parada que pueden ser las siguientes –
- La temperatura alcanza un valor especificado
- No hay cambio de estado durante un número especificado de iteraciones
.