Sensación comprimida

{\displaystyle \mathbf {y} =D\mathbf {x} donde queremos encontrar una solución para x {\displaystyle \mathbf {x} } }

.

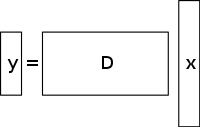
Para elegir una solución a un sistema de este tipo, hay que imponer restricciones o condiciones adicionales (como la suavidad) según convenga. En la detección comprimida, se añade la restricción de la escasez, permitiendo sólo soluciones que tengan un pequeño número de coeficientes no nulos. No todos los sistemas subdeterminados de ecuaciones lineales tienen una solución dispersa. Sin embargo, si existe una solución dispersa única para el sistema subdeterminado, entonces el marco de detección comprimida permite la recuperación de esa solución.

Método de solución / reconstrucción

La detección comprimida aprovecha la redundancia de muchas señales interesantes: no son puro ruido. En particular, muchas señales son escasas, es decir, contienen muchos coeficientes cercanos o iguales a cero, cuando se representan en algún dominio. Esta es la misma idea que se utiliza en muchas formas de compresión con pérdidas.

La detección comprimida suele comenzar con la toma de una combinación lineal ponderada de muestras, también llamada mediciones compresivas, en una base diferente de la base en la que se sabe que la señal es dispersa. Los resultados encontrados por Emmanuel Candès, Justin Romberg, Terence Tao y David Donoho, mostraron que el número de estas medidas compresivas puede ser pequeño y seguir conteniendo casi toda la información útil. Por lo tanto, la tarea de volver a convertir la imagen en el dominio deseado implica resolver una ecuación matricial infradeterminada, ya que el número de medidas compresivas tomadas es menor que el número de píxeles de la imagen completa. Sin embargo, si se añade la restricción de que la señal inicial es dispersa, se puede resolver este sistema de ecuaciones lineales infradeterminado.

La solución de mínimos cuadrados para este tipo de problemas consiste en minimizar el L 2 {\displaystyle L^{2}}

norma-es decir, minimizar la cantidad de energía en el sistema. Esto suele ser sencillo desde el punto de vista matemático (sólo implica una multiplicación de la matriz por el pseudoinverso de la base muestreada). Sin embargo, esto lleva a resultados pobres para muchas aplicaciones prácticas, para las cuales los coeficientes desconocidos tienen energía no nula.

Para hacer cumplir la restricción de escasez cuando se resuelve el sistema indeterminado de ecuaciones lineales, se puede minimizar el número de componentes no nulos de la solución. La función que cuenta el número de componentes no nulas de un vector se denominó L 0 {\displaystyle L^{0}}

«norma» por David Donoho.

Candès et al. demostraron que para muchos problemas es probable que la L 1 {\displaystyle L^{1}}

sea equivalente a la norma L 0 {\displaystyle L^{0}}

, en un sentido técnico: Este resultado de equivalencia permite resolver la norma L 1 {\displaystyle L^{1}}

, lo cual es más fácil que el problema de L 0 {pantalla L^{0}}

problem. Encontrar el candidato con el menor L 1 {\displaystyle L^{1}}

puede expresarse con relativa facilidad como un programa lineal, para el que ya existen métodos de solución eficientes. Cuando las mediciones pueden contener una cantidad finita de ruido, se prefiere el denoising de persecución de bases sobre la programación lineal, ya que preserva la dispersidad frente al ruido y puede resolverse más rápidamente que un programa lineal exacto.

Reconstrucción de CS basada en la variación total

Motivación y aplicaciones

Función de regularización de la TV

La variación total puede verse como un funcional no negativo de valor real definido en el espacio de funciones de valor real (para el caso de funciones de una variable) o en el espacio de funciones integrables (para el caso de funciones de varias variables). Para las señales, especialmente, la variación total se refiere a la integral del gradiente absoluto de la señal. En la reconstrucción de señales e imágenes, se aplica como regularización de la variación total, donde el principio subyacente es que las señales con excesivos detalles tienen una alta variación total y que la eliminación de estos detalles, conservando información importante como los bordes, reduciría la variación total de la señal y haría que el sujeto de la señal se acercara más a la señal original en el problema.

Para el propósito de la reconstrucción de señales e imágenes, l 1

se utilizan modelos de minimización. Otros enfoques también incluyen los mínimos cuadrados como se ha discutido antes en este artículo. Estos métodos son extremadamente lentos y devuelven una reconstrucción no muy perfecta de la señal. Los actuales modelos de regularización CS intentan resolver este problema incorporando priores de dispersión de la imagen original, uno de los cuales es la variación total (TV). Los enfoques convencionales de la TV están diseñados para dar soluciones constantes a trozos. Algunos de ellos incluyen (como ya se ha comentado) – la minimización l1 restringida, que utiliza un esquema iterativo. Este método, aunque es rápido, conduce posteriormente a un exceso de suavizado de los bordes que da lugar a bordes de imagen borrosos. Se han implementado métodos de TV con reponderación iterativa para reducir la influencia de grandes magnitudes de valores de gradiente en las imágenes. Esto se ha utilizado en la reconstrucción de tomografía computarizada (TC) como un método conocido como variación total que preserva los bordes. Sin embargo, como las magnitudes de gradiente se utilizan para la estimación de los pesos de penalización relativos entre la fidelidad de los datos y los términos de regularización, este método no es robusto al ruido y a los artefactos ni lo suficientemente preciso para la reconstrucción de la imagen/señal de la TC y, por lo tanto, no consigue preservar las estructuras más pequeñas.

Los últimos avances en este problema implican el uso de un refinamiento de TV direccional iterativo para la reconstrucción de CS. Este método tendría 2 etapas: la primera etapa estimaría y refinaría el campo de orientación inicial – que se define como una estimación inicial ruidosa a nivel de puntos, a través de la detección de bordes, de la imagen dada. En la segunda etapa, se presenta el modelo de reconstrucción CS utilizando el regularizador de TV direccional. A continuación se ofrecen más detalles sobre estos enfoques basados en la TV: minimización de l1 reponderada iterativamente, TV que preserva los bordes y modelo iterativo que utiliza el campo de orientación direccional y la TV.

Enfoques existentes

L 1 reponderada iterativamente {{displaystyle l_{1}}

minimización

En los modelos de reconstrucción de CS utilizando l 1 {{displaystyle l_{1}} restringido

minimización, los coeficientes más grandes son penalizados fuertemente en el l 1 {displaystyle l_{1}}

norm. Se propuso una formulación ponderada de l 1 {\displaystyle l_{1}}

minimización diseñada para penalizar más democráticamente los coeficientes no nulos. Se utiliza un algoritmo iterativo para construir los pesos adecuados. Cada iteración requiere resolver una l 1 {\displaystyle l_{1}}

problema de minimización encontrando el mínimo local de una función de penalización cóncava que se asemeja más a la l 0 {displaystyle l_{0}}

norm. Se introduce un parámetro adicional, normalmente para evitar transiciones bruscas en la curva de la función de penalización, en la ecuación iterativa para garantizar la estabilidad y para que una estimación nula en una iteración no conduzca necesariamente a una estimación nula en la siguiente. El método consiste esencialmente en utilizar la solución actual para calcular los pesos que se utilizarán en la siguiente iteración.

Ventajas y desventajas

Las primeras iteraciones pueden encontrar estimaciones de muestra inexactas, sin embargo este método reducirá la muestra en una etapa posterior para dar más peso a las estimaciones de señales más pequeñas que no son cero. Una de las desventajas es la necesidad de definir un punto de partida válido, ya que no siempre se puede obtener un mínimo global debido a la concavidad de la función. Otra desventaja es que este método tiende a penalizar uniformemente el gradiente de la imagen, independientemente de las estructuras subyacentes de la misma. Esto provoca un sobrealisado de los bordes, especialmente los de las regiones de bajo contraste, lo que conlleva posteriormente la pérdida de información de bajo contraste. Las ventajas de este método son: la reducción de la tasa de muestreo para señales dispersas; la reconstrucción de la imagen siendo robusta a la eliminación de ruido y otros artefactos; y el uso de muy pocas iteraciones. Esto también puede ayudar en la recuperación de imágenes con gradientes dispersos.

En la figura que se muestra a continuación, P1 se refiere al primer paso del proceso de reconstrucción iterativa, de la matriz de proyección P de la geometría del haz de abanico, que está restringida por el término de fidelidad de los datos. Puede contener ruido y artefactos, ya que no se realiza ninguna regularización. La minimización de P1 se resuelve mediante el método de mínimos cuadrados de gradiente conjugado. P2 se refiere al segundo paso del proceso de reconstrucción iterativo en el que se utiliza el término de regularización de variación total que preserva los bordes para eliminar el ruido y los artefactos, y así mejorar la calidad de la imagen/señal reconstruida. La minimización de P2 se realiza mediante un método simple de descenso de gradiente. La convergencia se determina probando, después de cada iteración, la positividad de la imagen, comprobando si f k – 1 = 0 {\displaystyle f^{k-1}=0}

para el caso en que f k – 1 < 0 {\displaystyle f^{k-1}<0}

(Nótese que f {\displaystyle f}

se refiere a los diferentes coeficientes de atenuación lineal de los rayos X en diferentes vóxeles de la imagen del paciente).

Detección comprimida basada en la variación total (TV) que preserva los bordes

Se trata de un algoritmo iterativo de reconstrucción de TC con regularización de TV que preserva los bordes para reconstruir imágenes de TC a partir de datos altamente submuestreados obtenidos en TC de baja dosis mediante niveles de corriente bajos (miliamperios). Para reducir la dosis de imagen, uno de los enfoques utilizados es reducir el número de proyecciones de rayos X adquiridas por los detectores del escáner. Sin embargo, estos datos de proyección insuficientes que se utilizan para reconstruir la imagen de TC pueden causar artefactos de rayas. Además, el uso de estas proyecciones insuficientes en los algoritmos estándar de TV acaba haciendo que el problema esté infradeterminado y, por lo tanto, conduce a infinitas soluciones posibles. En este método, se asigna una función ponderada de penalización adicional a la norma de TV original. Esto permite detectar más fácilmente las discontinuidades bruscas de intensidad en las imágenes y adaptar así el peso para almacenar la información de borde recuperada durante el proceso de reconstrucción de la señal/imagen.

controla la cantidad de suavizado que se aplica a los píxeles de los bordes para diferenciarlos de los que no lo son. El valor de σ {\displaystyle \sigma }

se modifica de forma adaptativa en función de los valores del histograma de la magnitud del gradiente, de forma que un determinado porcentaje de píxeles tenga valores de gradiente mayores que σ {\displaystyle \sigma }

. El término de variación total que preserva los bordes, por lo tanto, se vuelve más escaso y esto acelera la implementación. Se utiliza un proceso de iteración de dos pasos conocido como algoritmo de división hacia delante y hacia atrás. El problema de optimización se divide en dos subproblemas que se resuelven con el método de mínimos cuadrados de gradiente conjugado y el método de descenso de gradiente simple, respectivamente. El método se detiene cuando se ha logrado la convergencia deseada o si se alcanza el número máximo de iteraciones.

Ventajas y desventajas

Algunas de las desventajas de este método son la ausencia de estructuras menores en la imagen reconstruida y la degradación de la resolución de la imagen. Sin embargo, este algoritmo de TV con preservación de bordes requiere menos iteraciones que el algoritmo de TV convencional. Analizando los perfiles de intensidad horizontales y verticales de las imágenes reconstruidas, se observa que hay saltos bruscos en los puntos de borde y una fluctuación insignificante y menor en los puntos que no son de borde. Por lo tanto, este método conduce a un bajo error relativo y a una mayor correlación en comparación con el método de TV. También suprime y elimina eficazmente cualquier forma de ruido y artefactos de la imagen, como las rayas.

Modelo iterativo que utiliza un campo de orientación direccional y una variación total direccional

Para evitar el exceso de suavizado de los bordes y los detalles de la textura y obtener una imagen CS reconstruida que sea precisa y robusta frente al ruido y los artefactos, se utiliza este método. En primer lugar, se realiza una estimación inicial del campo de orientación puntual ruidoso de la imagen I

, d ^ {\displaystyle {\hat {d}}

, se obtiene. Este campo de orientación ruidoso se define para que pueda ser refinado en una etapa posterior para reducir las influencias del ruido en la estimación del campo de orientación. A continuación, se introduce una estimación de campo de orientación gruesa basada en el tensor de estructura que se formula como J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 22 ) {\displaystyle J_{{rho }(\nabla I_{sigma =G_{\rho }*(\nabla I_{\sigma })={{comienzo{pmatriz}J_{11}&J_{12}{J{12}&J_{22}{final{pmatriz}}.

. Aquí, J ρ {\displaystyle J_{\rho }}

se refiere al tensor de estructura relacionado con el punto de píxel de la imagen (i,j) que tiene una desviación estándar ρ {\displaystyle \rho }

. G {\displaystyle G}

se refiere al núcleo gaussiano ( 0 , ρ 2 ) {\displaystyle (0,\rho ^{2})}

con desviación estándar ρ {\displaystyle \rho }

. σ {\displaystyle \sigma }

se refiere al parámetro definido manualmente para la imagen I {\displaystyle I}

por debajo del cual la detección de bordes es insensible al ruido. ∇ I σ {\displaystyle \nabla I_{sigma }}

se refiere al gradiente de la imagen I {\displaystyle I}

y ( ∇ I σ ⊗ ∇ I σ ) {\displaystyle (\nabla I_{\sigma }\\a veces \nabla I_{\sigma })}

se refiere al producto tensorial obtenido mediante este gradiente.

El tensor de estructura obtenido se convoluciona con un núcleo gaussiano G {{displaystyle G}}.

para mejorar la precisión de la estimación de la orientación con σ {\displaystyle \sigma }

que se establece en valores altos para tener en cuenta los niveles de ruido desconocidos. Para cada píxel (i,j) de la imagen, el tensor de estructura J es una matriz simétrica y semidefinida positiva. Convolviendo todos los píxeles de la imagen con G

, se obtienen los vectores propios ortonormales ω y υ de la matriz J {displaystyle J}

. ω apunta en la dirección de la orientación dominante que tiene el mayor contraste y υ apunta en la dirección de la orientación de la estructura que tiene el menor contraste. La estimación inicial gruesa del campo de orientación d ^ {\displaystyle {\hat {d}}

se define como d ^ {displaystyle {\hat {d}}

= υ. Esta estimación es precisa en los bordes fuertes. Sin embargo, en bordes débiles o en regiones con ruido, su fiabilidad disminuye.

Para superar este inconveniente, se define un modelo de orientación refinado en el que el término de datos reduce el efecto del ruido y mejora la precisión, mientras que el segundo término de penalización con la norma L2 es un término de fidelidad que asegura la precisión de la estimación gruesa inicial.

Este campo de orientación se introduce en el modelo de optimización de variación total direccional para la reconstrucción del CS a través de la ecuación m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}\lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}.

. X {\displaystyle \mathrm {X} }

es la señal objetiva que hay que recuperar. Y es el vector de medición correspondiente, d es el campo de orientación refinado iterativo y Φ {\displaystyle \Phi }

es la matriz de medición CS. Este método se somete a unas cuantas iteraciones que finalmente conducen a la convergencia. d ^ {\displaystyle {\hat {d}}

es la estimación aproximada del campo de orientación de la imagen reconstruida X k – 1 {\displaystyle X^{k-1}}

de la iteración anterior (para comprobar la convergencia y el rendimiento óptico posterior, se utiliza la iteración anterior). Para los dos campos vectoriales representados por X {\displaystyle \mathrm {X} }

y d {\displaystyle d}

, X ∙ d {\displaystyle \mathrm {X} \bullet d}

se refiere a la multiplicación de los respectivos elementos vectoriales horizontales y verticales de X {\displaystyle \mathrm {X} }

y d {\displaystyle d}

, seguido de su posterior adición. Estas ecuaciones se reducen a una serie de problemas de minimización convexa que luego se resuelven con una combinación de métodos de división de variables y lagrangiano aumentado (solucionador rápido basado en FFT con una solución de forma cerrada). El lagrangiano aumentado se considera equivalente a la iteración de Bregman dividida, que garantiza la convergencia de este método. El campo de orientación, d se define como igual a ( d h , d v ) {\displaystyle (d_{h},d_{v})}

, donde d h , d v {\displaystyle d_{h},d_{v}}

definen las estimaciones horizontales y verticales de d {\displaystyle d}

.

El método lagrangiano aumentado para el campo de orientación, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}\lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}

, implica inicializar d h , d v , H , V {\displaystyle d_{h},d_{v},H,V}

y luego encontrar el minimizador aproximado de L 1 {\displaystyle L_{1}}

con respecto a estas variables. A continuación se actualizan los multiplicadores lagrangianos y el proceso iterativo se detiene cuando se alcanza la convergencia. Para el modelo iterativo de refinamiento de la variación total direccional, el método lagrangiano aumentado implica inicializar X , P , Q , λ P , λ Q {\displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}.

.

Aquí, H , V , P , Q {\displaystyle H,V,P,Q}

son variables de nueva introducción donde H {\displaystyle H}

= ∇ d h {\displaystyle \nabla d_{h}}

, V {\displaystyle V}

= ∇ d v {\displaystyle \nabla d_{v}}

, P {\displaystyle P}

= ∇ X {\displaystyle \nabla \mathrm {X} }

, y Q {\displaystyle Q}

= P ∙ d {\displaystyle P\bullet d}

. λ H , λ V , λ P , λ Q {\displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}

son los multiplicadores lagrangianos para H , V , P , Q {\displaystyle H,V,P,Q}

. Para cada iteración, el minimizador aproximado de L 2 {\displaystyle L_{2}}

con respecto a las variables ( X , P , Q {\displaystyle \mathrm {X} ,P,Q}

). Y como en el modelo de refinamiento de campo, se actualizan los multiplicadores lagrangianos y se detiene el proceso iterativo cuando se alcanza la convergencia.

Para el modelo de refinamiento del campo de orientación, los multiplicadores lagrangianos se actualizan en el proceso iterativo como sigue:

( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) {\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {\displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k})}

Para el modelo iterativo de refinamiento de la variación total direccional, los multiplicadores lagrangianos se actualizan como sigue:

( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}(P^{k}-\nabla (\mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) {\displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}\bullet d)}

Aquí, γ H , γ V , γ P , γ Q {\displaystyle \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}

son constantes positivas.

Ventajas y desventajas

A partir de las métricas de relación señal-ruido (PSNR) e índice de similitud estructural (SSIM) y de las imágenes de referencia conocidas para comprobar el rendimiento, se concluye que la variación total direccional iterativa tiene un mejor rendimiento de reconstrucción que los métodos no iterativos en la preservación de las áreas de borde y textura. El modelo de refinamiento del campo de orientación juega un papel importante en esta mejora del rendimiento, ya que aumenta el número de píxeles sin dirección en el área plana, mientras que mejora la consistencia del campo de orientación en las regiones con bordes.