Barysentriset koordinaatit

kirjoittaja
Geometria > Koordinaattigeometria >
Geometria > Tasogeometria > Tasogeometria > Kolmiot > Kolmion ominaisuudet >

Barysentriset koordinaatit ovat lukujen kolmioita (t_1,t_2,t_3), jotka vastaavat viitekolmion DeltaA_1A_2A_3 kärkipisteisiin sijoitettuja massoja. Nämä massat määrittävät sitten pisteen P, joka on kolmen massan geometrinen keskipiste ja joka tunnistetaan koordinaateilla (t_1,t_2,t_3). Kolmion kärkipisteet ovat (1,0,0), (0,1,0) ja (0,0,1). Barysentriset koordinaatit löysi Möbius vuonna 1827 (Coxeter 1969, s. 217; Fauvel et al. 1993).

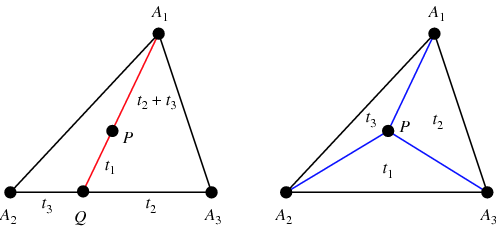
Barycentric

Löytääksemme mielivaltaisen pisteen P biosentriset koordinaatit löydämme t_2 ja t_3 pisteestä Q, joka sijaitsee suoran A_1P ja sivun A_2A_3 leikkauspisteessä, ja määritetään sitten t_1 massaksi pisteessä A_1, joka tasapainottaa massan t_2+t_3 pisteessä Q, jolloin massan P keskipisteeksi tulee P (vasen kuva). Lisäksi kolmioiden DeltaA_1A_2P, DeltaA_1A_3P ja DeltaA_2A_3P pinta-alat ovat verrannollisia P:n barysentrisiin koordinaatteihin t_3, t_2 ja t_1 (oikea kuva; Coxeter 1969, s. 217).

Barysentriset koordinaatit ovat homogeenisia, joten

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

for mu!=0.

Barykeskikoordinaatteja, jotka on normalisoitu siten, että niistä tulee osakulmioiden todellisia pinta-aloja, kutsutaan homogeenisiksi barykeskikoordinaateiksi. Barykeskikoordinaatteja, jotka on normalisoitu siten, että

t_1+t_2+t_3=1,
(2)

siten, että koordinaatit antavat alakolmioiden pinta-alat, jotka on normalisoitu alkuperäisen kolmion pinta-alalla, kutsutaan areaalikoordinaateiksi (Coxeter 1969, s. 218). Barysentristen ja areaalikoordinaattien avulla voidaan antaa erityisen tyylikkäitä todistuksia geometrisille lauseille, kuten Routhin lauseelle, Cevan lauseelle ja Menelaoksen lauseelle (Coxeter 1969, s. 219-221).

(Ei välttämättä homogeeniset) barysentriset koordinaatit useille tavallisille keskipisteille on koottu seuraavaan taulukkoon. Taulukossa a, b ja c ovat kolmion sivupituuksia ja s on sen puolimittari.

kolmion keskipiste barysentriset koordinaatit
kehäkeskipiste O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
eksentteri J_B (a,-b,c)
eksentteri J_C (a,b,-c)
Gergonnen piste Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incenter I (a,b,c)
Nagelin piste Na (s-a,s-b,s-c)
ortokeskus H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
symmediaanipiste K (a^2,b^2,c^2)
kolmion keskipiste G (1,1,1)

Barysentrisissä koordinaateissa suoralla on lineaarinen homogeeninen yhtälö. Erityisesti pisteitä (r_1,r_2,r_3) ja (s_1,s_2,s_3) yhdistävällä suoralla on yhtälö

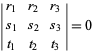|r_1 r_2 r_3; s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 ja 57; Coxeter 1969, s. 219; Bottema 1982). Jos kolmion DeltaP_1P_2P_3 kärkipisteillä P_i on barysentriset koordinaatit (x_i,y_i,z_i), niin kolmion pinta-ala on

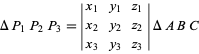DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Jätä kommentti