Nämä ovat stokastisia oppimisprosesseja, joilla on rekurrenssirakenne, ja ne ovat perusta ANN:ssä käytetyille varhaisille optimointitekniikoille. Boltzmann-koneen keksivät Geoffrey Hinton ja Terry Sejnowski vuonna 1985. Lisää selkeyttä voidaan havaita Hintonin sanoista Boltzmann-koneesta.
”Yllättävä piirre tässä verkossa on se, että se käyttää vain paikallisesti saatavilla olevaa tietoa. Painon muutos riippuu vain niiden kahden yksikön käyttäytymisestä, joita se yhdistää, vaikka muutos optimoi globaalia toimenpidettä.” – Ackley, Hinton 1985.
Joitakin tärkeitä seikkoja Boltzmann-koneesta –
-
Ne käyttävät rekurrenssirakennetta.
-
Ne koostuvat stokastisista neuroneista, joilla on yksi kahdesta mahdollisesta tilasta, joko 1 tai 0.
-
Osa neuroneista on adaptiivisia (vapaa tila) ja osa kiinnittyneitä (jäädytetty tila).
-
Jos sovellamme simuloitua hehkutusta (simulated annealing) diskreettiin Hopfield-verkkoon, niin siitä tulee Boltzmannin kone.
Boltzmann-koneen tavoite
Boltzmann-koneen päätarkoitus on optimoida ongelman ratkaisu. Boltzmann-koneen tehtävänä on optimoida kyseiseen ongelmaan liittyvät painot ja määrät.
Arkkitehtuuri
Seuraavassa kaaviossa on esitetty Boltzmann-koneen arkkitehtuuri. Kaaviosta käy selvästi ilmi, että kyseessä on kaksiulotteinen joukko yksiköitä. Tässä yksiköiden välisten yhteyksien painot ovat -p, jossa p > 0. Itsekytkentöjen painot ovat b, jossa b > 0.
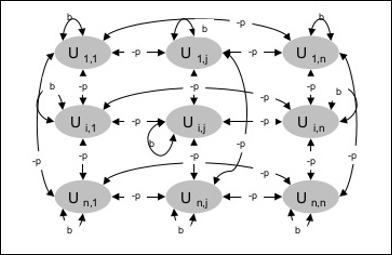
Koulutusalgoritmi
Koska tiedämme, että Boltzmann-koneilla on kiinteät painot, näin ollen koulutusalgoritmia ei tarvita, koska meidän ei tarvitse päivittää verkon painoja. Verkon testaamiseksi meidän on kuitenkin asetettava painot sekä löydettävä konsensusfunktio (CF).
Boltzmannin koneessa on joukko yksiköitä Ui ja Uj ja niillä on kaksisuuntaiset yhteydet.
-
Harkitsemme kiinteää painoa sanotaan wij.
-
wij ≠ 0, jos Ui ja Uj ovat kytkeytyneitä.
-
Painotetuissa kytkennöissä on myös olemassa symmetria, i.eli wij = wji.
-
wii on myös olemassa, eli yksiköiden välillä olisi itsekytkentä.
-
Jollekin yksikölle Ui sen tila ui olisi joko 1 tai 0.
Boltzmann-koneen päätavoitteena on maksimoida konsensusfunktio (CF), joka voidaan antaa seuraavalla relaatiolla
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
Nyt kun tila muuttuu joko 1:stä 0:ksi tai 0:sta 1:ksi, niin konsensuksen muutos voidaan antaa seuraavalla relaatiolla –
$$$\\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Tässä ui on tämänhetkinen tila Ui.
Kertoimen (1 – 2ui) vaihtelu saadaan seuraavasta relaatiosta –
$$(1\:-\:2u_{i})\:=\:\alku{cases}+1, & U_{i}\:on\:nykyinen\:off\\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
Yksikkö Ui ei yleensä muuta tilaansa, mutta jos se muuttaa, niin silloin tieto pysyy paikallisesti yksikössä. Tämän muutoksen myötä myös verkon konsensus kasvaisi.
Verkon todennäköisyys hyväksyä yksikön tilan muutos saadaan seuraavasta relaatiosta –
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Tässä T on ohjaava parametri. Se pienenee, kun CF saavuttaa maksimiarvon.
Testausalgoritmi
Vaihe 1 – Initialisoidaan seuraavat, jotta voidaan aloittaa harjoittelu –
- Painot, jotka edustavat ongelman rajoitteita
- Säätöparametri T
Vaihe 2 – Jatketaan vaiheita 3-8, kun pysäytysehto ei ole totta.
Vaihe 3 – Suorita vaiheet 4-7.
Vaihe 4 – Oletetaan, että yksi tiloista on muuttanut painoa ja valitaan kokonaisluvut I, J satunnaisarvoiksi välillä 1-n.
Vaihe 5 – Lasketaan konsensuksen muutos seuraavasti –
$$\\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$$
Vaihe 6 – Lasketaan todennäköisyys, että tämä verkko hyväksyisi tilamuutoksen
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Vaihe 7 – Hyväksy tai hylkää tämä muutos seuraavasti –
Tapaus I – jos R < AF, hyväksy muutos.
Tapaus II – jos R ≥ AF, hylkää muutos.
Tässä R on satunnaisluku väliltä 0 ja 1.
Vaihe 8 – Pienennetään säätöparametria (lämpötilaa) seuraavasti –
T(uusi) = 0.95T(vanha)
Vaihe 9 – Testataan pysäytysehdot, jotka voivat olla seuraavat –
- Lämpötila saavuttaa määritellyn arvon
- Tilassa ei tapahdu muutosta tiettyyn määrään iteraatioita
.