Biography

Brahmagupta (598-668 CE)
Suuri 7. vuosisadalla elänyt intialainen matemaatikko ja tähtitieteilijä Brahmagupta kirjoitti eräitä tärkeitä teoksia sekä matematiikasta että tähtitieteestä. Hän oli kotoisin Luoteis-Intian Rajasthanin osavaltiosta (hänestä käytetään usein nimitystä Bhillamalacarya, Bhillamalan opettaja), ja hänestä tuli myöhemmin Keski-Intiassa sijaitsevan Ujjainin tähtitieteellisen observatorion johtaja. Suurin osa hänen teoksistaan on kirjoitettu elliptisillä säkeistöillä, mikä oli tuohon aikaan yleinen käytäntö intialaisessa matematiikassa, ja näin ollen niissä on jonkinlainen runollinen sävy.
Näyttää todennäköiseltä, että 8. vuosisadan abbasidikalifi Al-Mansur toi Brahmaguptan teokset, erityisesti hänen kuuluisimman tekstinsä, ”Brahmasphutasiddhantan”, vastaperustettuun oppimiskeskukseensa Bagdadiin Tigris-joen rannalle, ja tarjosi näin tärkeän linkin intialaisen matematiikan ja tähtitieteen sekä islamilaisessa maailmassa alkaneen tieteen ja matematiikan nousun välille.
Aritmetiikkaa käsittelevässä teoksessaan Brahmagupta selitti, miten kokonaisluvun kuutio ja kuutiojuuri löydetään, ja antoi sääntöjä, jotka helpottavat neliöiden ja neliöjuurien laskemista. Hän antoi myös sääntöjä murtolukujen viidenlaisten yhdistelmien käsittelyyn. Hän antoi n ensimmäisen luonnollisen luvun neliöiden summaksi n(n + 1)(2n + 1)⁄ 6 ja n ensimmäisen luonnollisen luvun kuutioiden summaksi (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Käsittele nollaa lukuna

Brahmaguptan säännöt nollan ja negatiivisten lukujen käsittelyyn
Brahmaguptan nerokkuus tuli kuitenkin esiin hänen käsittelyssään (tuolloin suhteellisen uuden) luvun nolla käsitteestä. Vaikka nolla liitetään usein myös 7. vuosisadan intialaiselle matemaatikolle Bhaskara I:lle, hänen ”Brahmasphutasiddhantansa” on luultavasti varhaisin tunnettu teksti, jossa nollaa käsiteltiin omana lukunaan eikä pelkkänä sijaislukuna, kuten babylonialaiset tekivät, tai määrän puutteen symbolina, kuten kreikkalaiset ja roomalaiset tekivät.
Brahmagupta loi matemaattiset perussäännöt nollan käsittelylle (1 + 0 = 1; 1 – 0 = 1; ja 1 x 0 = 0), vaikka hänen käsityksensä nollalla jakamisesta oli epätäydellinen (hän ajatteli, että 1 ÷ 0 = 0). Lähes 500 vuotta myöhemmin, 1200-luvulla, toinen intialainen matemaatikko, Bhaskara II, osoitti, että vastauksen pitäisi olla ääretön eikä nolla (sillä perusteella, että 1 voidaan jakaa äärettömään määrään nollan kokoisia paloja), ja tätä vastausta pidettiin oikeana vuosisatojen ajan. Tämä logiikka ei kuitenkaan selitä, miksi 2 ÷ 0, 7 ÷ 0 jne. pitäisi myös olla nolla – modernin näkemyksen mukaan nollalla jaettu luku on itse asiassa ”määrittelemätön” (eli siinä ei ole mitään järkeä).
Brahmaguptan näkemys luvuista abstrakteina kokonaisuuksina eikä vain laskemiseen ja mittaamiseen tarkoitettuina kokonaisuuksina mahdollisti hänelle vielä yhden valtavan käsitteellisen harppauksen, jolla olisi syvällisiä seurauksia tulevaan matematiikkaan. Aiemmin esimerkiksi summaa 3 – 4 pidettiin joko merkityksettömänä tai parhaimmillaan vain nollana. Brahmagupta kuitenkin tajusi, että voisi olla olemassa sellainenkin asia kuin negatiivinen luku, jota hän kutsui ”velaksi” ”ominaisuuden” vastakohtana. Hän selvitti sääntöjä negatiivisten lukujen käsittelyyn (esim. negatiivinen kertaa negatiivinen on positiivinen, negatiivinen kertaa positiivinen on negatiivinen jne.)
Lisäksi hän huomautti, että kvadraattisilla yhtälöillä (esimerkiksi tyyppiä x2 + 2 = 11) voisi teoriassa olla kaksi mahdollista ratkaisua, joista toinen voisi olla negatiivinen, koska 32 = 9 ja -32 = 9. Yleisten lineaaristen yhtälöiden ja kvadraattisten yhtälöiden ratkaisuja koskevan työnsä lisäksi Brahmagupta meni vielä pidemmälle tarkastelemalla samanaikaisten yhtälöiden järjestelmiä (yhtälöryhmiä, jotka sisältävät useita muuttujia) ja ratkaisemalla kvadraattisia yhtälöitä, joissa on kaksi tuntematonta, jotain sellaista, jota länsimaissa ei edes harkittu ennen kuin vasta tuhat vuotta myöhemmin, kun Fermat pohdiskeli vastaavia ongelmia vuonna 1657.
Brahmaguptan lause syklisistä nelikulmioista
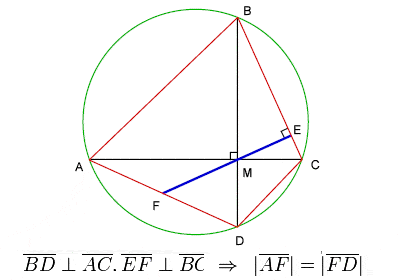
Brahmaguptan lause syklisistä nelikulmioista
Brahmagupta jopa yritti kirjoittaa ylös nämä varsin abstraktit käsitteet, käyttämällä värien nimien alkukirjaimia kuvaamaan yhtälöidensä tuntemattomia, mikä on yksi varhaisimmista esimerkeistä siitä, mitä nykyään kutsumme algebraksi.
Brahmagupta omisti huomattavan osan työstään geometrialle ja trigonometrialle. Hän vahvisti √10 (3,162277) hyvän käytännön approksimaation π:lle (3,141593) ja antoi kaavan, joka nykyään tunnetaan nimellä Brahmaguptan kaava, syklisen nelikulmion pinta-alalle sekä kuuluisan lauseen syklisen nelikulmion diagonaaleista, jota yleensä kutsutaan nimellä Brahmaguptan lause.
| << Takaisin intialaiseen matematiikkaan | Edelleen Madhava >> |