C-tilasto:

ROC-käyrä > C-statistiikka

Voit lukea tämän artikkelin ensin: Mikä on ROC-käyrä (Receiver Operating Characteristic)?

Mikä on C-statistiikka?

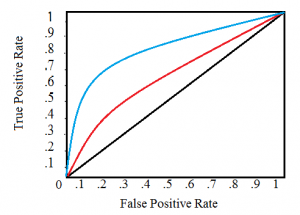
Konkordanssitilasto vastaa ROC-käyrän alapuolella olevaa pinta-alaa.

C-statistiikka (jota kutsutaan joskus ”konkordanssi”-statistiikaksi tai C-indeksiksi) on mittari, jonka avulla mitataan logistisen regressiomallin binääristen lopputuloksien sopivuutta. Kliinisissä tutkimuksissa C-statistiikka antaa todennäköisyyden, jolla satunnaisesti valitulla potilaalla, joka koki tapahtuman (esim. sairauden tai tilan), oli korkeampi riskipistemäärä kuin potilaalla, joka ei ollut kokenut tapahtumaa. Se on yhtä suuri kuin ROC-käyrän (Receiver Operating Characteristic) alle jäävä pinta-ala, ja se vaihtelee välillä 0,5-1.

• Alle 0,5 jäävä arvo tarkoittaa erittäin huonoa mallia.
• Arvo 0,5 tarkoittaa, että malli ei ennusta lopputulosta paremmin kuin satunnainen sattuma.
• Arvot yli 0.7 viittaavat hyvään malliin.
• Arvot yli 0.8 viittaavat vahvaan malliin.
• Arvo 1 tarkoittaa, että malli ennustaa täydellisesti ne ryhmän jäsenet, jotka kokevat tietyn lopputuloksen ja ne, jotka eivät.

C-statistiikkaa ei käytetä kovin usein, koska se antaa vain yleisen käsityksen mallista; ROC-käyrä sisältää paljon enemmän tietoa tarkkuudesta, herkkyydestä ja spesifisyydestä.

Painotus

Painotettua c-indeksiä käytetään silloin, kun positiivisen lopputuloksen (kuten syöpäkokeen) ennustamatta jättämisen kustannukset ovat suuremmat kuin negatiivisen lopputuloksen oikeasta ennustamisesta saatava hyöty. Painotus rankaisee malleja, jotka johtavat pieniin todennäköisyyseroihin positiivisten ja negatiivisten lopputulosten osalta, mutta ei muuta C-statistiikan arvoa. Sitä voidaan käyttää myös ositetun satunnaisotannan mukauttamiseen.

Tilastollinen merkitsevyys

Kuten useimmat tilastot, C-statistiikka on joskus yhdistetty luottamusväliin. Esimerkiksi tulos voi olla 0,63 ja luottamusväli 0,53-0,73). Yleensä mikään tulos ei ole merkitsevä, jos se sisältää 0,5, vaikka se sisältäisi kyseisen C-tilaston. Esimerkiksi tulos 0,63, jonka luottamusväli on 0,43-0,83, ei olisi merkitsevä, koska se sisältää 0,5 tällä alueella.

Viite:
Hosmer DW, Lemeshow S. Applied Logistic Regression (2nd Edition). New York, NY: John Wiley & Sons; 2000.

——————————————————————————

Tarvitsetko apua kotitehtävän tai kokeen kysymyksen kanssa? Chegg Studyn avulla saat kysymyksiisi vaiheittaiset ratkaisut alan asiantuntijalta. Ensimmäiset 30 minuuttia Chegg-opettajan kanssa ovat ilmaisia!