Introduction
Ensyymin aktiiviset kohdat koostuvat tavallisesti aminohappojäännöksistä; riippuen siitä, mitkä aminohappojäännökset ovat läsnä, substraatin spesifisyys voi vaihdella suuresti. pH-tasosta riippuen entsyymin fysikaaliset ominaisuudet (lähinnä sähkövaraukset) voivat muuttua. Muutos sähköisessä varauksessa voi muuttaa aktiivisen alueen aminohappojäämien ja saapuvan substraatin välistä vuorovaikutusta. Näin ollen substraatti voi sitoutua aktiiviseen kohtaan vetysidoksen tai van der Waalsin voimien avulla. Kun substraatti sitoutuu aktiiviseen kohtaan, se muodostaa entsyymi-substraatti-kompleksin, joka sitten osallistuu muihin kemiallisiin reaktioihin.
Jotta entsyymi olisi aktiivinen ja energeettisesti suotuisa, jotta kemiallinen reaktio etenisi, substraatin on sitouduttava entsyymin ”aktiiviseen kohtaan”. Aktiivinen alue voidaan ajatella lukoksi ja substraatti avaimeksi; tämä tunnetaan lukko-avain-mallina. Avain (substraatti) on työnnettävä sisään ja käännettävä (kemiallinen reaktio), minkä jälkeen lukko (entsyymi) avautuu (tuotteiden tuotanto). Huomaa, että entsyymillä voi olla useampi kuin yksi aktiivinen alue. Toinen teoria aktiivisen paikan ja substraatin välisestä suhteesta on indusoidun sopivuuden teoria, joka on täysin päinvastainen kuin lukko ja avain -teoria (jossa aktiivinen paikka on näennäisesti joustamaton). Indusoidun sovituksen teoriassa entsyymin aktiivinen alue on hyvin joustava ja muuttaa konformaatiotaan vain silloin, kun substraatti sitoutuu siihen.
Ensiymit toimivat katalysaattorina alentamalla entsyymi-substraatti-kompleksin aktivoitumisen Gibbsin vapaata energiaa. Alla on kaksi kuvaa, joissa esitetään entsymaattinen perusreaktio katalyytin kanssa ja ilman katalyyttiä:
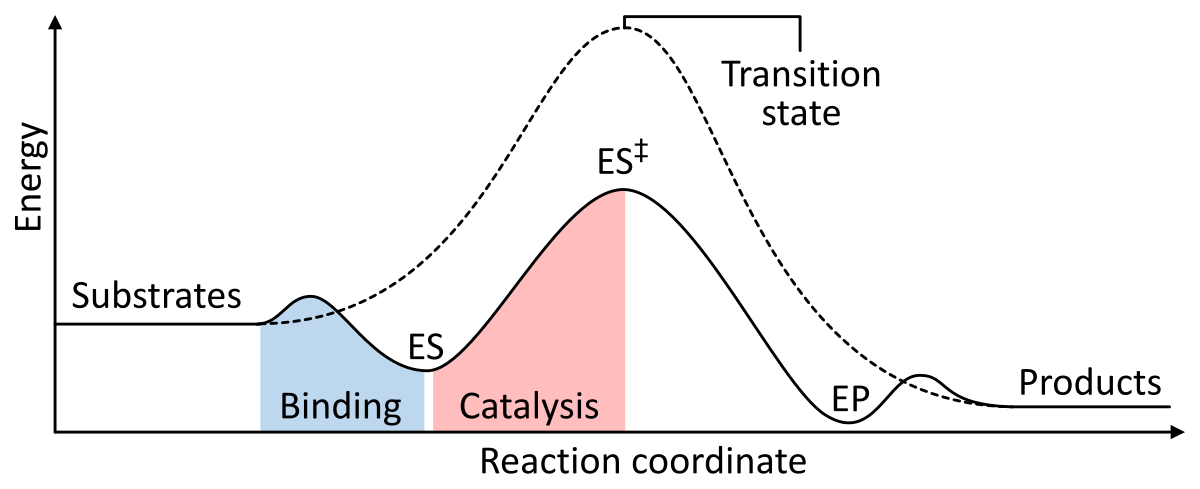
Kuva 1: Kemiallisen reaktion vaiheiden energiat. Katalysoimatta (katkoviiva) substraatit tarvitsevat paljon aktivaatioenergiaa päästäkseen siirtymätilaan, joka sitten hajoaa matalamman energian tuotteiksi. Kun entsyymi katalysoi (yhtenäinen viiva), entsyymi sitoo substraatteja (ES), sitten stabiloi siirtymätilan (ES‡) vähentääkseen aktivoitumisenergiaa, joka tarvitaan tuotteiden (EP) tuottamiseen, jotka lopulta vapautuvat. from Wikipedia.
Ensyymin tehokkuus voidaan määrittää seuraavasti: Tarkastellaan yksinkertaista entsymaattista reaktiota:
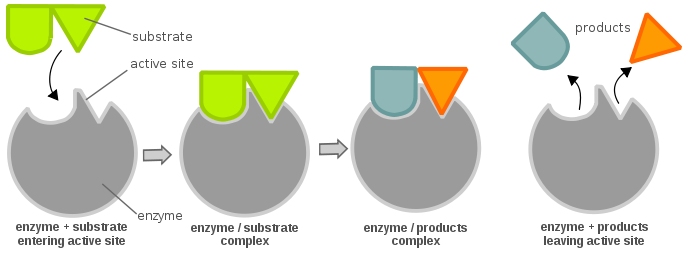
Saksalainen biokemisti Leonor Michaelis ja kanadalainen biokemisti Maud Menten johtivat tätä systeemiä kuvaavan yhtälön, joka tunnetaan myöhemmin nimellä ”Michaelis-Menten-yhtälö” ja joka on esitetty alla:
\}{K_M + } \tag{1}\]
Tämä yhtälö antaa reaktion nopeuden tietyllä substraattikonsentraatiolla olettaen, että tunnetaan Vmax, joka on suurin nopeus, jolla reaktio voi edetä, ja KM, Michaelis-vakio. Michaelis-Mentenin käytännön sovelluksessa V0 kuitenkin usein mitataan, ja Vmax havaitaan kyllästymisenä tai tasona datan kuvaajassa. Koska substraattikonsentraatio tunnetaan, KM on yleensä kiinnostava laskennallinen arvo.
For \(K_M\), assume \(V_0= \dfrac{V_{max}}{2}\):
\}{K_M + } \tag{2}\]
\) \dfrac{V_{max}}{2} = V_{max} \tag{3}\]
\ = \dfrac{V_{max}}{\dfrac{V_{max}}{2}} \tag{4} \tag{5}\]
\ = 2 \tag{5}\]
\ \tag{6}\]
Michaelis-vakiota voidaan ajatella nopeutena, jolla substraatti irtoaa entsyymistä, mikä voi tapahtua joko tapahtumissa substraatti-entsyymikompleksi muuttuu tuotteeksi tai substraatti irtoaa entsyymistä. KM voidaan esittää yhtälönä.
\
Jolloin k-1 on nopeusvakio, jolla substraatti irtoaa entsyymistä, jolloin entsyymi-substraatti-kompleksi dissosioituu, k2 on nopeusvakio, jolla substraatti-entsyymikompleksi häviää ja muuttuu tuotteeksi, ja K1 on nopeusvakio, jolla substraatti-entsyymikompleksi muodostuu. KM voidaan siis katsoa substraatti-entsyymikompleksin häviämisnopeudeksi jaettuna substraatti-entsyymikompleksin muodostumisnopeudella, joka on taso, jolla puolet substraatista on sitoutunut entsyymiin. KM on hyödyllinen indikaattori inhibiittorin läsnäololle, koska voimme tarkastella KM:n muutoksia ja verrata niitä kontrolliin (biologiset järjestelmät, joissa tiedämme, että inhibiittoria ei esiinny lainkaan). KM on riippuvainen muuttuja, ja sen arvo voi muuttua monista syistä, kuten järjestelmän pH-tasosta, lämpötilasta tai mistä tahansa muusta olosuhteesta, joka voi vaikuttaa kemialliseen reaktioon. Pieni KM osoittaa, että substraatilla on suuri affiniteetti entsyymiä kohtaan.
Michaelis-Mentenin yhtälö on käyttökelpoisin entsyymin tehokkuutta mitattaessa, jos v0 piirretään vasteena , seuraavasti:
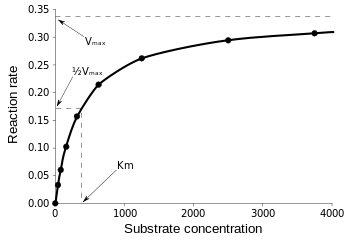
Kuvio 3: Reaktionopeuden ja Michaelis-Mentenin vakion kaavio. Wikipediasta.
Vmax on maksiminopeus, jolla reaktio voi kulkea riippumatta , mikä tarkoittaa, että vaikka substraattia lisättäisiin lisää, reaktio ei voi kulkea yhtään nopeammin. Tämä johtuu siitä, että Vmax:ssa kaikki entsyymin aktiiviset paikat ovat varattuja. Kaikkien entsyymikineettisten yhtälöiden eri muotoja koskevien selitysten jälkeen päädymme päätelmään katalyyttisestä tehokkuudesta. Viitaten takaisin kuvaan 3, meillä on:
\_o}{\dfrac{k_{-1} + k_2}{k_1}{k_1} + }\right) \tag{8}\]
Huomaa, että \(k_2\) kuvaa irreversiibeliä reaktiota vastakohtana tasapainoilmaisulle, kun sitä verrataan k-1:een ja k1:een. k2 tunnetaan tässä myös nimellä kcat, entsyymin katalyyttinen tehokkuus. Edellisen keskustelun perusteella v0 on mitattu reaktionopeus eli tuotteen muodostuminen ajan kuluessa, joten voidaan päätellä, että yhtälö näyttäisi seuraavalta:
\}{dt} = k_2_0 \tag{9}\]
Jossa 0 on entsyymin kokonaispitoisuus.
Tiedetään myös, että VMax havaitaan, kun kaikki entsyymi-substraatti-kompleksi häviää ja muuttuu tuotteiksi, joten voimme tehdä seuraavan oletuksen:
\_0 \tag{10} \]
ja uudelleenjärjestelyn jälkeen saadaan tämä yhtälö:
\_0} \tag{11}\]
Tämä on katalyyttisen tehokkuuden laskentayhtälö, jota käytetään sen jälkeen, kun olemme saaneet tietoja kokeista ja kun olemme käyttäneet Michaelis-Mentenin yhtälöä. Kun kcat on suurempi, entsyymi on tehokas, koska entsyymiä tarvitaan vähemmän.