Aliterminoimaton lineaarinen järjestelmä
Aliterminoidussa lineaarisessa yhtälösysteemissä on enemmän tuntemattomia kuin yhtälöitä, ja sillä on yleensä ääretön määrä ratkaisuja. Alla olevassa kuvassa on esitetty tällainen yhtälösysteemi y = D x {\displaystyle \mathbf {y} =D\mathbf {x} }

jossa haluamme löytää ratkaisun x:lle {\displaystyle \mathbf {x} }

.
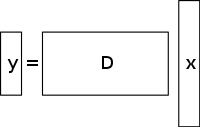
Voidaksemme valita ratkaisun tällaiseen systeemiin, meidän on asetettava ylimääräisiä rajoituksia tai ehtoja (kuten tasaisuus) tarpeen mukaan. Tiivistetyssä aistimisessa lisätään harvinaisuusrajoitus, joka sallii vain sellaiset ratkaisut, joissa on pieni määrä nollasta poikkeavia kertoimia. Kaikilla alideterminoituneilla lineaarisilla yhtälösysteemeillä ei ole harvaa ratkaisua. Jos alideterminoituneelle järjestelmälle on kuitenkin olemassa ainutkertainen harva ratkaisu, kompressoidun aistimisen avulla tämä ratkaisu voidaan palauttaa.
Ratkaisu / rekonstruktiomenetelmä

Puristettu aistiminen hyödyntää monien mielenkiintoisten signaalien redundanssia – ne eivät ole puhdasta kohinaa. Erityisesti monet signaalit ovat harvalukuisia, eli ne sisältävät monia kertoimia, jotka ovat lähellä nollaa tai yhtä suuria kuin nolla, kun ne esitetään jollakin alueella. Tämä on sama oivallus, jota käytetään monissa häviöllisen pakkauksen muodoissa.
Puristettu aistiminen alkaa tyypillisesti ottamalla näytteiden painotettu lineaarinen yhdistelmä, jota kutsutaan myös kompressiivisiksi mittauksiksi, eri perustassa kuin perustassa, jossa signaalin tiedetään olevan harva. Emmanuel Candèsin, Justin Rombergin, Terence Taon ja David Donohon löytämät tulokset osoittivat, että näiden kompressiivisten mittausten määrä voi olla pieni ja silti sisältää lähes kaiken hyödyllisen informaation. Näin ollen kuvan muuntaminen takaisin aiottuun alueeseen edellyttää alideterminoituneen matriisiyhtälön ratkaisemista, koska otettujen kompressiomittausten määrä on pienempi kuin koko kuvan pikselien määrä. Kuitenkin lisäämällä rajoitus, että alkusignaali on harva, voidaan ratkaista tämä alideterminoitunut lineaarinen yhtälösysteemi.
Tällaisten ongelmien pienimmän neliösumman ratkaisu on minimoida L 2 {\displaystyle L^{2}}

normi – eli minimoidaan systeemin energiamäärä. Tämä on yleensä matemaattisesti yksinkertaista (sisältää vain matriisikertomuksen näytteenottoperustan pseudoinversiolla). Tämä johtaa kuitenkin huonoihin tuloksiin monissa käytännön sovelluksissa, joissa tuntemattomilla kertoimilla on nollasta poikkeavaa energiaa.
Harvinaisuusrajoituksen valvomiseksi, kun ratkaistaan alideterminoitua lineaarista yhtälösysteemiä, voidaan minimoida ratkaisun nollasta poikkeavien komponenttien lukumäärä. Vektorin nollasta poikkeavien komponenttien lukumäärää laskevaa funktiota kutsuttiin L 0 {\displaystyle L^{0}}

”normiksi” David Donohon toimesta.
Candès et al. osoittivat, että monissa ongelmissa on todennäköistä, että L 1 {\displaystyle L^{1}}

normi vastaa L 0 {\displaystyle L^{0}}

normia teknisessä mielessä: Tämän ekvivalenssituloksen avulla voidaan ratkaista L 1 {\displaystyle L^{1}}

-ongelman, joka on helpompi kuin L 0 {\displaystyle L^{0}}

problem. Sellaisen ehdokkaan löytäminen, jolla on pienin L 1 {\displaystyle L^{1}}

normia voidaan suhteellisen helposti ilmaista lineaarisena ohjelmana, jolle on jo olemassa tehokkaita ratkaisumenetelmiä. Kun mittaukset voivat sisältää äärellisen määrän kohinaa, basis pursuit denoising -menetelmää käytetään mieluummin kuin lineaarista ohjelmointia, koska se säilyttää harvinaisuuden kohinan vallitessa ja se voidaan ratkaista nopeammin kuin tarkka lineaarinen ohjelma.
Total variation based CS reconstruction
Motivaatio ja sovellukset
Tv-regularisoinnin rooli
Totaalinen variaatio voidaan nähdä ei-negatiivisena reaaliarvoisena funktionaalina, joka on määritelty reaaliarvoisten funktioiden avaruudessa (yhden muuttujan funktioiden tapauksessa) tai integroitavien funktioiden avaruudessa (usean muuttujan funktioiden tapauksessa). Erityisesti signaalien osalta kokonaisvaihtelulla tarkoitetaan signaalin absoluuttisen gradientin integraalia. Signaalien ja kuvien rekonstruktiossa sitä sovelletaan kokonaisvaihtelun regularisointina, jossa perusperiaatteena on, että signaaleilla, joissa on liikaa yksityiskohtia, on suuri kokonaisvaihtelu ja että näiden yksityiskohtien poistaminen säilyttäen tärkeää informaatiota, kuten reunat, pienentäisi signaalin kokonaisvaihtelua ja tekisi signaalin kohteen lähemmäksi alkuperäistä signaalia ongelmassa.
Signaalien ja kuvien rekonstruktiota varten l 1 {\displaystyle l1}

käytetään minimointimalleja. Muita lähestymistapoja ovat myös pienimmän neliösumman mallit, kuten tässä artikkelissa on aiemmin käsitelty. Nämä menetelmät ovat erittäin hitaita ja palauttavat signaalista ei-niin-täydellisen rekonstruktion. Nykyiset CS-säännöstelymallit pyrkivät ratkaisemaan tämän ongelman sisällyttämällä alkuperäisen kuvan harvinaisuuspriorit, joista yksi on kokonaisvariaatio (TV). Perinteiset TV-lähestymistavat on suunniteltu antamaan kappalemääräisiä vakioratkaisuja. Joitakin näistä ovat (kuten edellä käsitellään) – rajoitettu l1-minimointi, jossa käytetään iteratiivista järjestelmää. Vaikka tämä menetelmä on nopea, se johtaa myöhemmin reunojen liialliseen silottamiseen, mikä johtaa kuvan reunojen epätarkkuuteen. TV-menetelmiä, joissa on iteratiivinen uudelleenpainotus, on toteutettu kuvissa esiintyvien suurten gradienttiarvojen vaikutuksen vähentämiseksi. Tätä on käytetty tietokonetomografian (CT) rekonstruktiossa menetelmänä, joka tunnetaan nimellä edge-preserving total variation. Koska gradientin suuruusluokkia käytetään datan uskollisuuden ja regularisointiehtojen välisten suhteellisten rangaistuspainojen estimointiin, tämä menetelmä ei kuitenkaan ole kestävä kohinan ja artefaktien suhteen eikä riittävän tarkka CS-kuvan/signaalin rekonstruktiossa, eikä se näin ollen pysty säilyttämään pienempiä rakenteita.
Viimeaikainen edistys tässä ongelmassa käsittää iteratiivisesti suunnatun TV-jalostuksen käyttämisen CS-rekonstruktiossa. Menetelmässä on kaksi vaihetta: ensimmäisessä vaiheessa estimoidaan ja tarkennetaan alkuperäistä suuntakenttää, joka määritellään tietyn kuvan reunojen havaitsemisen avulla tapahtuvaksi kohinaiseksi pistemäiseksi alkuarvioksi. Toisessa vaiheessa CS:n rekonstruktiomalli esitetään käyttämällä suuntakohtaista TV-säännöstelyä. Lisätietoja näistä TV-pohjaisista lähestymistavoista – iteratiivisesti uudelleen painotettu l1 minimointi, reunoja säilyttävä TV ja iteratiivinen malli, jossa käytetään suuntaa-antavaa orientaatiokenttää ja TV:tä – on esitetty jäljempänä.
Olemassa olevat lähestymistavat
Iteratiivisesti uudelleen painotettu l 1 {\displaystyle l_{1}}


minimointi

Cs:n rekonstruktiomalleissa, joissa käytetään rajoitettua {\displaystyle l_{1}}} l{³”a}{³”a}:tä.

minimointia, suurempia kertoimia rangaistaan voimakkaasti l 1 {\displaystyle l_{1}}

norm. Ehdotettiin painotettua muotoilua l 1 {\displaystyle l_{1}}

minimointi, joka on suunniteltu rankaisemaan nollasta poikkeavia kertoimia demokraattisemmin. Sopivien painojen rakentamiseen käytetään iteratiivista algoritmia. Jokaisessa iteraatiossa on ratkaistava yksi l 1 {\displaystyle l_{1}}

minimointiongelma etsimällä sellaisen koveran rangaistusfunktion paikallinen minimi, joka muistuttaa enemmän l 0 {\displaystyle l_{0}}

norm. Iteratiiviseen yhtälöön lisätään lisäparametri, jolla yleensä vältetään jyrkkiä siirtymiä rangaistusfunktion käyrällä, jotta varmistetaan stabiilius ja jotta nollaestimaatti yhdessä iteraatiossa ei välttämättä johda nollaestimaattiin seuraavassa iteraatiossa. Menetelmässä käytetään pääasiassa nykyistä ratkaisua seuraavassa iteraatiossa käytettävien painojen laskemiseen.
Hyötyjä ja haittoja
Varhaisissa iteraatioissa saattaa löytyä epätarkkoja otosestimaatteja, mutta tämä menetelmä pienentää otosta myöhemmässä vaiheessa antaakseen suuremman painoarvon pienemmille nollasta poikkeaville signaaliestimaateille. Yksi haittapuolista on tarve määritellä kelvollinen aloituspiste, koska globaalia minimiä ei välttämättä saavuteta joka kerta funktion konkavuuden vuoksi. Toinen haittapuoli on se, että tällä menetelmällä on taipumus rankaista kuvan gradienttia yhdenmukaisesti taustalla olevista kuvan rakenteista riippumatta. Tämä aiheuttaa reunojen, erityisesti matalakontrastisten alueiden reunojen liiallista tasoittumista, mikä johtaa matalakontrastisen informaation häviämiseen. Menetelmän etuja ovat muun muassa seuraavat: näytteenottotaajuuden pienentäminen harvojen signaalien osalta, kuvan rekonstruointi, joka on kestävä kohinan ja muiden artefaktien poistamisen suhteen, ja hyvin harvojen iteraatioiden käyttö. Tämä voi auttaa myös sellaisten kuvien palauttamisessa, joissa on harvat gradientit.
Alhaalla esitetyssä kuvassa P1 viittaa iteratiivisen rekonstruktioprosessin ensimmäiseen vaiheeseen, viuhkamaisen sädekehän geometrian projektiomatriisiin P, jota rajoittaa datan uskollisuustermi. Tämä voi sisältää kohinaa ja artefakteja, koska regularisointia ei suoriteta. P1:n minimointi ratkaistaan konjugoidun gradientin pienimmän neliösumman menetelmällä. P2 viittaa iteratiivisen rekonstruktioprosessin toiseen vaiheeseen, jossa käytetään reunoja säilyttävää kokonaisvaihtelun regularisointitermiä kohinan ja artefaktien poistamiseksi ja siten rekonstruoidun kuvan/signaalin laadun parantamiseksi. P2:n minimointi tehdään yksinkertaisella gradienttilaskeutumismenetelmällä. Konvergenssi määritetään testaamalla jokaisen iteraation jälkeen kuvan positiivisuus tarkistamalla, onko f k – 1 = 0 {\displaystyle f^{k-1}=0}

tapauksessa, jossa f k – 1 < 0 {\displaystyle f^{k-1}<0}

(Huomaa, että f {\displaystyle f}

viittaa erilaisiin röntgensäteilyn lineaarisiin vaimennuskertoimiin potilaskuvan eri vokseleissa).
Reunoja säilyttävä kokonaisvaihteluun (TV) perustuva kompressiivinen tunnistaminen

Tämä on iteratiivinen CT-rekonstruktiointialgoritmi, jossa käytetään reunoja säilyttävää TV-säännöstelyä CT-kuvausten rekonstruoimiseksi voimakkaasti alinäytteistetystä aineistosta, joka saadaan matala-annoksellisella CT-kuvauslaitteella pienillä virranvoimakkuustasoilla (milliampereillä). Kuvantamisannoksen pienentämiseksi yksi käytetyistä lähestymistavoista on vähentää skannerin ilmaisimien ottamien röntgenprojektioiden määrää. Tämä riittämätön projisointitieto, jota käytetään CT-kuvan rekonstruoimiseen, voi kuitenkin aiheuttaa raidallisia artefakteja. Lisäksi näiden riittämättömien projektioiden käyttäminen tavanomaisissa TV-algoritmeissa tekee ongelmasta alideterminoidun ja johtaa siten äärettömän moneen mahdolliseen ratkaisuun. Tässä menetelmässä alkuperäiseen TV-normiin liitetään ylimääräinen painotettu rangaistusfunktio. Näin voidaan helpommin havaita jyrkät epäjatkuvuudet kuvien intensiteetissä ja siten mukauttaa painoa talteen otetun reunainformaation tallentamiseksi signaalin/kuvan rekonstruointiprosessin aikana. Parametri σ {\displaystyle \sigma }

ohjaa reunoilla oleviin pikseleihin sovellettavan tasoituksen määrää, jotta ne voidaan erottaa reunojen ulkopuolisista pikseleistä. Arvo σ {\displaystyle \sigma }

muutetaan adaptiivisesti gradientin suuruuden histogrammin arvojen perusteella siten, että tietyllä prosenttimäärällä pikseleistä gradientin arvot ovat suurempia kuin σ {\displaystyle \sigma }

. Reunat säilyttävä kokonaisvaihtelutermi muuttuu siten harvemmaksi, mikä nopeuttaa toteutusta. Käytetään kaksivaiheista iterointiprosessia, joka tunnetaan nimellä forward-backward splitting algorithm. Optimointiongelma jaetaan kahteen osaongelmaan, jotka ratkaistaan konjugoidun gradientin pienimmän neliösumman menetelmällä ja yksinkertaisen gradientin laskeutumismenetelmän avulla. Menetelmä lopetetaan, kun haluttu konvergenssi on saavutettu tai jos iteraatioiden enimmäismäärä on saavutettu.
Hyötyjä ja haittoja
Tämän menetelmän haittoja ovat muun muassa pienempien rakenteiden puuttuminen rekonstruoidusta kuvasta ja kuvan resoluution heikkeneminen. Tämä reunoja säilyttävä TV-algoritmi vaatii kuitenkin vähemmän iteraatioita kuin perinteinen TV-algoritmi. Analysoitaessa rekonstruoitujen kuvien vaaka- ja pystysuuntaisia intensiteettiprofiileja voidaan havaita, että reunapisteissä on jyrkkiä hyppäyksiä ja muissa kuin reunapisteissä vähäistä, vähäistä vaihtelua. Näin ollen tämä menetelmä johtaa pieneen suhteelliseen virheeseen ja korkeampaan korrelaatioon verrattuna TV-menetelmään. Se myös vaimentaa ja poistaa tehokkaasti kaikenlaista kuvakohinaa ja kuvan artefakteja, kuten raitaisuutta.
Iteratiivinen malli, jossa käytetään suuntautunutta orientaatiokenttää ja suuntautunutta kokonaisvaihtelua
Menetelmällä estetään reunojen ja tekstuurin yksityiskohtien liiallinen tasoittuminen ja saadaan rekonstruoitua CS-kuva, joka on tarkka ja vastustuskykyinen kohinalle ja artefakteille. Ensin tehdään alkuestimaatti kuvan kohinaisesta pistemäisestä orientaatiokentästä I {\displaystyle I}

, d ^ {\displaystyle {\hat {d}}}

, saadaan. Tämä kohinainen orientaatiokenttä määritellään siten, että sitä voidaan myöhemmässä vaiheessa tarkentaa kohinan vaikutusten vähentämiseksi orientaatiokentän estimoinnissa. Tämän jälkeen otetaan käyttöön karkea orientaatiokentän estimointi, joka perustuu rakennetensoriin, joka muotoillaan seuraavasti: J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 22 ) {\displaystyle J_{\rho }(\nabla I__{sigma })=G_{\rho }*(\nabla I_{\sigma }\times \nabla I_{\sigma })={\begin{pmatrix}J_{11}&J_{12}\\\J_{12}&J_{22}\end{pmatrix}}}

. Tässä J ρ {\displaystyle J_{\rho}}

viittaa kuvan pikselipisteeseen (i,j) liittyvään rakennetensoriin, jonka keskihajonta ρ {\displaystyle \rho }

. G {\displaystyle G}

viittaa Gaussin ytimeen ( 0 , ρ 2 ) {\displaystyle (0,\rho ^{2})}

, jonka keskihajonta ρ {\displaystyle \rho }

. σ {{\displaystyle \sigma}

viittaa kuvan I käsin määriteltyyn parametriin {\displaystyle I}

, jonka alapuolella reunantunnistus on epäherkkä kohinalle. ∇ I σ {\displaystyle \nabla I_{\sigma }}

viittaa kuvan kaltevuuteen I {\displaystyle I}

ja ( ∇ I σ ⊗ ∇ I σ ) {\displaystyle (\nabla I_{\sigma }\otimes \nabla I_{\sigma })}

viittaa tämän gradientin avulla saatuun tensorituloon.
Tuloksena saatu rakennetensor konvolvoidaan Gaussin ytimellä G {\displaystyle G}

orientaatioestimaatin tarkkuuden parantamiseksi σ {\displaystyle \sigma } kanssa.

asetetaan korkeisiin arvoihin tuntemattoman kohinan huomioon ottamiseksi. Kunkin kuvan pikselin (i,j) osalta rakennetensor J on symmetrinen ja positiivinen puolimäärätön matriisi. Kaikkien kuvan pikseleiden konvoluutio G:llä {\displaystyle G}

, saadaan J {\displaystyle J} ortonormaalit ominaisvektorit ω ja υ.

-matriisin. ω osoittaa suurimman kontrastin omaavan dominoivan orientaation suuntaan ja υ osoittaa pienimmän kontrastin omaavan rakenneorientaation suuntaan. Orientaatiokentän karkea alkuarvio d ^ {\displaystyle {\hat {d}}}

määritellään seuraavasti: d ^ {\displaystyle {\hat {d}}}

= υ. Tämä arvio on tarkka vahvoilla reunoilla. Heikoilla reunoilla tai alueilla, joilla on kohinaa, sen luotettavuus kuitenkin heikkenee.
Tämän epäkohdan poistamiseksi määritellään tarkennettu orientaatiomalli, jossa datatermi vähentää kohinan vaikutusta ja parantaa tarkkuutta, kun taas toinen L2-normin mukainen rangaistustermi on uskollisuustermi, joka varmistaa alkuperäisen karkean estimaatin tarkkuuden.
Tämä orientaatiokenttä tuodaan CS:n rekonstruktiossa käytettävään suuntaa-antavaan kokonaisvaihtelun optimointimalliin yhtälön avulla: m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}

. X {\displaystyle \mathrm {X} }

on tavoitesignaali, joka pitää palauttaa. Y on vastaava mittausvektori, d on iteratiivisesti tarkennettu orientaatiokenttä ja Φ {\displaystyle \Phi }

on CS-mittausmatriisi. Tämä menetelmä käy läpi muutamia iteraatioita, jotka lopulta johtavat konvergenssiin. d ^ {\displaystyle {\hat {d}}}

on rekonstruoidun kuvan X k – 1 suuntauskentän likiarvio {\displaystyle X^{k-1}}

edellisestä iteraatiosta (konvergenssin ja myöhemmän optisen suorituskyvyn tarkistamiseksi käytetään edellistä iteraatiota). Kahdelle vektorikentälle, joita edustavat X {\displaystyle \mathrm {X} }

ja d {\displaystyle d}

, X ∙ d {\displaystyle \mathrm{X} \bullet d}

tarkoittaa X {\displaystyle \mathrm {X} } vastaavien vaaka- ja pystyvektorielementtien kertomista.

ja d {\displaystyle d}

ja sen jälkeen niiden yhteenlasku. Nämä yhtälöt pelkistetään sarjaksi koveria minimointiongelmia, jotka sitten ratkaistaan yhdistelmällä muuttujien pilkkomista ja augmented Lagrangen (FFT-pohjainen nopea ratkaisija, jolla on suljetun muodon ratkaisu) menetelmiä. Sitä (Augmented Lagrangian) pidetään ekvivalenttina jaetun Bregmanin iteraation kanssa, joka varmistaa tämän menetelmän konvergenssin. Suuntauskentän d määritellään olevan yhtä suuri kuin ( d h , d v ) {\displaystyle (d_{h},d_{v})}

, missä d h , d v {\displaystyle d_{h}},d_{v}}}

määrittelevät horisontaaliset ja vertikaaliset estimaatit d {\displaystyle d}

.

Augmented Lagrangen menetelmä orientaatiokentälle, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}

, sisältää alustuksen d h , d v , H , V {\displaystyle d_{h},d_{v},H,V}}

ja sen jälkeen etsitään likimääräinen minimoija L 1 {\displaystyle L_{1}}

näiden muuttujien suhteen. Tämän jälkeen päivitetään Lagrangen kertoimet ja iteratiivinen prosessi lopetetaan, kun konvergenssi on saavutettu. Iteratiivisen suuntaa-antavan kokonaisvaihtelun hienosäätömallin osalta augmentoidussa Lagrangen menetelmässä alustetaan X , P , Q , λ P , λ Q {\displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}}

.
Tässä, H , V , P , Q {\displaystyle H,V,P,Q}

ovat äskettäin käyttöön otettuja muuttujia, joissa H {\displaystyle H}

= ∇ d h {\displaystyle \nabla d_{h}}

, V {\displaystyle V}

= ∇ d v {\displaystyle \nabla d_{v}}

, P {\displaystyle P}

= ∇ X {\displaystyle \nabla \mathrm {X} }

, ja Q {\displaystyle Q}

= P ∙ d {\displaystyle P\bullet d}

. λ H , λ V , λ P , λ Q {\displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}}

ovat Lagrangen kertoimet H , V , P , Q {\displaystyle H,V,P,Q}}

. Jokaisella iteraatiolla likimääräinen minimoija L 2 {\displaystyle L_{2}}

muuttujien ( X , P , Q {\displaystyle \mathrm {X} ,P,Q}} suhteen.

) lasketaan. Ja kuten kentän tarkennusmallissa, lagrangen kertoimet päivitetään ja iteratiivinen prosessi lopetetaan, kun konvergenssi on saavutettu.
Ohjauskentän tarkennusmallissa Lagrangen kertoimet päivitetään iteratiivisessa prosessissa seuraavasti:
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) {\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {\displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k})}

Iteratiivisen suuntaa-antavan totaalisen variaation hienosäätömallissa päivitetään Lagrangin kertoimet seuraavasti:
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}(P^{k}-\nabla (\mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) {\displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}\bullet d)}

Tässä, γ H , γ V , γ P , γ Q {\displaystyle \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}

ovat positiivisia vakioita.
Hyötyjä ja haittoja
Signaali-kohinasuhteen huippuarvon (PSNR) ja rakenteellisen samankaltaisuusindeksin (SSIM) mittareiden sekä suorituskyvyn testaamiseen käytettävien tunnettujen maastokuvien perusteella voidaan päätellä, että iteratiivisella suuntautuneella kokonaismuunnoksella on ei-iteratiivisia menetelmiä parempi rekonstruktiosuorituskyky reuna- ja tekstuurialueiden säilyttämisen suhteen. Suuntakentän tarkennusmallilla on merkittävä rooli suorituskyvyn paranemisessa, sillä se lisää suuntaamattomien pikselien määrää tasaisella alueella ja parantaa samalla suuntauskentän johdonmukaisuutta alueilla, joilla on reunoja.