Learning Objective
1. Muunna yhdestä yksiköstä toiseen samantyyppiseen yksikköön.
Luvussa 2.2 ”Yksiköiden ilmaiseminen” näytimme joitakin esimerkkejä siitä, miten alkuperäiset yksiköt voidaan korvata toisilla samantyyppisillä yksiköillä, jotta saadaan helpommin hahmotettava lukuarvo. Tässä jaksossa formalisoimme tämän prosessin.
Harkitaan yksinkertaista esimerkkiä: Kuinka monta jalkaa on neljässä jaardissa? Useimmat ihmiset vastaavat lähes automaattisesti, että 4 jaardissa on 12 jalkaa. Miten sinä olet tehnyt tämän määrityksen? No, jos yhdessä jaardissa on 3 jalkaa ja on 4 jaardia, niin 4 × 3 = 12 jalkaa on 4 jaardissa.
Tämä on tietysti oikein, mutta se on epävirallista. Muodollistetaan se tavalla, jota voidaan soveltaa yleisemmin. Tiedämme, että 1 jaardi (yd) vastaa 3 jalkaa (ft):
1 yd = 3 jalkaa
Matematiikassa tätä lauseketta kutsutaan tasa-arvoksi. Algebran säännöt sanovat, että voit muuttaa (eli kertoa tai jakaa tai lisätä tai vähentää) yhtälön (kunhan et jaa nollalla) ja uusi lauseke on edelleen yhtälö. Jos esimerkiksi jaamme molemmat puolet kahdella, saamme tulokseksi
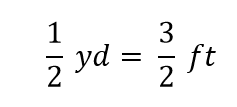
Näemme, että puolet metristä on yhtä kuin 3/2 eli puolitoista jalkaa – jotain, jonka myös tiedämme olevan totta, joten edellä oleva yhtälö on edelleen yhtälö. Palataan alkuperäiseen yhtälöön, jaetaanpa yhtälön molemmat puolet 1 yardilla (luku ja yksikkö):
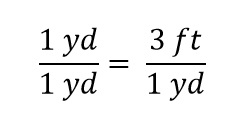
Yhtälö on algebran sääntöjen mukaan edelleen yhtälö. Vasen murtoluku on yhtä kuin 1. Siinä on sama määrä sekä osoittajassa että nimittäjässä, joten sen on oltava yhtä suuri kuin 1. Suureet osoittajassa ja nimittäjässä kumoavat sekä lukumäärän että yksikön:
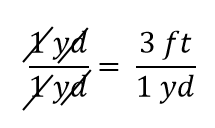
Kun kaikki kumoaa murtoluvussa, murtoluku pienenee 1:ksi:
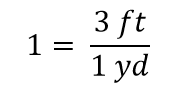
Meillä on lauseke 3 ft / 1 yd, joka on yhtä kuin 1. Tämä on outo tapa kirjoittaa 1, mutta siinä on järkeä: 3 ft on yhtä kuin 1 yd, joten osoittajan ja nimittäjän määrät ovat sama määrä, joka vain ilmaistaan eri yksiköillä. Ilmaisua 3 ft1 yd kutsutaan muuntokertoimeksi, ja sitä käytetään muodollisesti muuttamaan suureen yksikkö toiseksi yksiköksi. (Prosessia, jossa yksiköt muunnetaan näin muodollisesti, kutsutaan joskus dimensioanalyysiksi tai kerroinmerkintämenetelmäksi.)
Katsoaksemme, miten tämä tapahtuu, lähdetään liikkeelle alkuperäisestä suureesta:
4 yd
Kerrotaan nyt tämä suure luvulla 1. Kun kerrot mitä tahansa luvulla 1, et muuta suureen arvoa. Sen sijaan, että kertoisimme vain 1:llä, kirjoitetaan 1 3 ft1 yd:
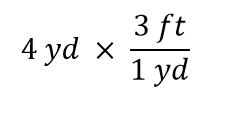
Termi 4 yd voidaan ajatella 4 yd/1:ksi; eli sitä voidaan ajatella murtolukuna, jonka nimittäjässä on 1. Kyseessä on siis murtolukujen kertominen. Jos murtoluvun osoittajassa ja nimittäjässä esiintyy sama asia, ne kumoutuvat. Tässä tapauksessa se, mikä kumoaa, on yksikkö yard:
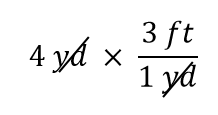
Se on kaikki, mitä voimme kumota. Kerrotaan ja jaetaan nyt kaikki luvut saadaksemme lopullisen vastauksen: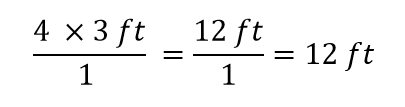
Jälleen saamme vastaukseksi 12 ft, aivan kuten alun perin. Mutta tässä tapauksessa käytimme muodollisempaa menettelyä, jota voidaan soveltaa useisiin ongelmiin.
Miten monta millimetriä on 14,66 m:ssä? Vastataksemme tähän kysymykseen meidän on muodostettava muuntokerroin millimetrien ja metrien välille ja sovellettava sitä oikein alkuperäiseen suureeseen. Aloitetaan millimetrin määritelmästä, joka on
1 mm = 1/1 000 m
Tätä 1/1 000 tarkoittaa etuliite milli-. Useimmille ihmisille on mukavampi työskennellä ilman murtolukuja, joten kirjoitamme tämän yhtälön uudelleen tuomalla 1 000 yhtälön toisen puolen osoittajaan:
1 000 mm = 1 m
Konstruoimme nyt muuntokertoimen jakamalla yhden suureen molemmille puolille. Mutta nyt herää kysymys: millä suureella jaamme? Osoittautuu, että meillä on kaksi vaihtoehtoa, ja näistä kahdesta vaihtoehdosta saamme erilaiset muuntokertoimet, joista molemmat ovat yhtä suuria kuin 1:
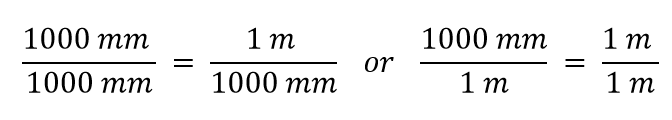
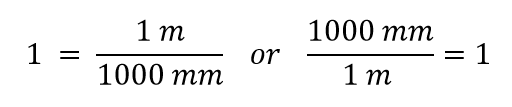
Kumpaa muuntokerrointa käytämme? Vastaus perustuu siihen, mistä yksiköstä haluat päästä eroon lähtömäärässäsi. Määrämme alkuperäinen yksikkö on metriä, jonka haluamme muuntaa millimetreiksi. Koska alkuperäisen yksikön oletetaan olevan osoittajassa, siitä eroon pääsemiseksi haluamme metriyksikön nimittäjään; silloin ne kumoutuvat. Siksi käytämme toista muuntokerrointa. Peruuttaessamme yksiköt ja suorittaessamme matematiikan saamme
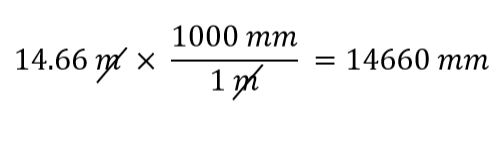
Huomaa, kuinka m peruuntuu, jolloin jäljelle jää millimetri, joka on kiinnostava yksikkö.
Kyky rakentaa ja soveltaa oikeita muuntokertoimia on erittäin tehokas matemaattinen tekniikka kemiassa. Sinun on hallittava tämä tekniikka, jos aiot menestyä tällä ja tulevilla kursseilla.
Esimerkki 7
- Muunnetaan 35,9 kL litroiksi.
- Muunnetaan 555 nm metreiksi.
Ratkaisu
-
Hyödynnämme sitä, että 1 kL = 1 000 L. Kahdesta määriteltävästä muuntokertoimesta toimii muunnos 1 000 L/1 kL. Soveltamalla tätä muuntokerrointa saadaan
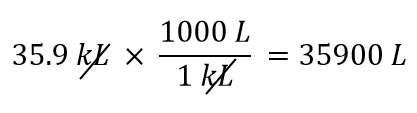
-
Hyödynnämme sitä tosiasiaa, että 1 nm = 1/1.000.000.000.000 m, jonka kirjoitamme uudelleen muotoon 1.000.000.000 nm = 1 m tai 109 nm = 1 m. Kahdesta mahdollisesta muuntokertoimesta sopivassa muuntokertoimessa on nm:n suuruinen yksikkö nimittäjässä: 1 m/109 nm. Soveltamalla tätä muuntokerrointa saamme
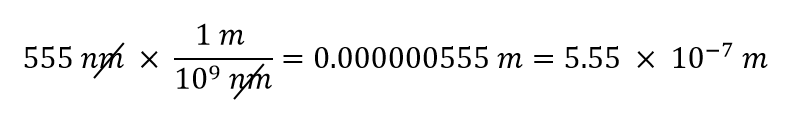
Viimeisessä vaiheessa ilmaisimme vastauksen tieteellisessä merkintätavassa.
Testaa itsesi
- Muunnos 67.08 μL litroiksi.
- Muunna 56,8 m kilometreiksi.
Vastaukset
- 6,708 × 10-5 L
- 5,68 × 10-2 km
Mitä tapahtuu, jos meillä on johdettu yksikkö, joka on useamman kuin yhden yksikön tulo, kuten m2? Oletetaan, että haluamme muuntaa neliömetrit neliösenttimetreiksi? Tärkeintä on muistaa, että m2 tarkoittaa m × m, mikä tarkoittaa, että johdetussa yksikössämme on kaksi metriyksikköä. Tämä tarkoittaa, että meidän on sisällytettävä kaksi muuntokerrointa, yksi kummallekin yksikölle. Jos haluamme esimerkiksi muuntaa 17,6 m2 neliösenttimetreiksi, suoritamme muunnoksen seuraavasti:
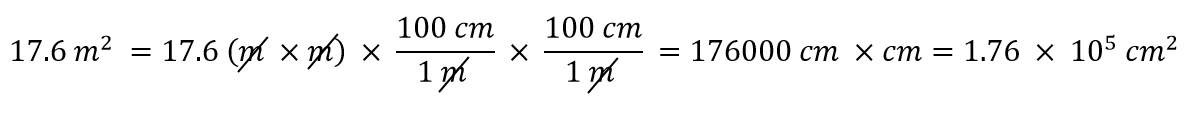
Esimerkki 8
Minkä verran kuutiosenttimetrejä 0.883 m3?
Ratkaisu
Kun eksponentti on 3, meillä on kolme pituusyksikköä, joten laajemmassa merkityksessä meidän on käytettävä kolmea muuntokerrointa metrien ja senttimetrien välillä. Näin ollen meillä on
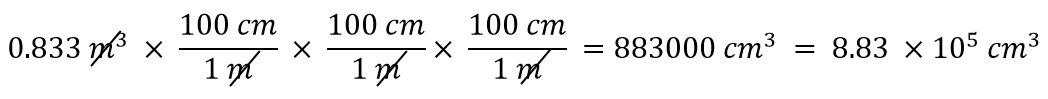
Tulee sinun osoittaa itsellesi, että kolme metriyksikköä todellakin kumoutuvat.
Testaa itsesi
Miten monta kuutiomillimetriä on 0,0923 m3:ssä?
Vastaus
9,23 × 107 mm3
Esitettäkö, että yksikkö, jonka haluat muuntaa, on johdetun yksikön nimittäjässä; mitä sitten? Silloin muuntokertoimessa yksikön, jonka haluat poistaa, on oltava osoittajassa. Tämä kumoaa alkuperäisen yksikön nimittäjässä ja tuo uuden yksikön nimittäjään. Seuraava esimerkki havainnollistaa tätä tilannetta.
Esimerkki 9
Muunnetaan 88,4 m/min metreiksi/sekunniksi.
Ratkaisu
Haluamme muuttaa nimittäjässä olevan yksikön minuuteista sekunneiksi. Koska yhdessä minuutissa on 60 sekuntia (60 s = 1 min), rakennamme muuntokertoimen niin, että poistettava yksikkö, minuutit, on osoittajassa: 1 min/60 s. Sovelletaan ja suoritetaan matematiikka:
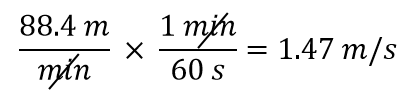
Huomaa, että 88,4 menee automaattisesti osoittajaan. Tämä johtuu siitä, että minkä tahansa luvun voidaan ajatella olevan 1:llä jaetun murtoluvun osoittajassa.
Testaa itsesi
Muunna 0,203 m/min metreiksi/sekunniksi.
Vastaus
0.00338 m/s tai 3,38 × 10-3 m/s
Kuvio 2.8 Kuinka nopea on nopea?

Lähde: ”Grapevine snail ”by Jürgen Schoneris licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.