Kokoonpuristuvuuskerroin (kaasut)

kirjoittaja
From Knowino
Tämä on tarkistettu versio tästä sivusta

Jumppaa osoitteeseen: Se on mitta siitä, kuinka paljon todellisen kaasun termodynaamiset ominaisuudet poikkeavat ideaalikaasulta odotetuista ominaisuuksista. Sitä voidaan ajatella todellisen kaasun todellisen tilavuuden ja ideaalikaasun ennustaman tilavuuden suhteena samassa lämpötilassa ja paineessa kuin todellinen tilavuus.

Ideaalikaasulle Z:n arvo on aina 1. Todellisille kaasuille arvo voi poiketa positiivisesti tai negatiivisesti riippuen kaasun molekyylien välisten voimien vaikutuksesta. Mitä lähempänä reaalikaasu on kriittistä pistettään tai kyllästymispistettään, sitä suuremmat ovat kaasun poikkeamat ideaalisesta käyttäytymisestä.

Kuvan 1 ylempi kuvaaja havainnollistaa, miten kokoonpuristuvuuskerroin vaihtelee eri kaasuilla samassa lämpötilassa ja paineessa. Alempi kuvaaja havainnollistaa, miten kaasun (esimerkiksi metaanin) kokoonpuristuvuuskerroin tietyssä paineessa vaihtelee lämpötilan mukaan.

Tässä artikkelissa käsitellään vain kaasujen kokoonpuristuvuuskerrointa eikä siinä syvennytä nesteiden tai höyryn ja nesteen seosten kokoonpuristuvuuteen.

  • 1 Kaasujen kokoonpuristuvuusarvojen määrittäminen
    • 1.1 Yleistetyt kokoonpuristuvuuslukujen kuvaajat puhtaille kaasuille
    • 1.2 Yleistetyt kokoonpuristuvuuslukujen kuvaajat kaasuseoksille
    • 1.3 Van der Waalsin yhtälö
      • 1.3.1 Van der Waalsin yhtälön modifioidut versiot
        • 1.3.1.1 Redlich-Kwong
        • 1.3.1.2 Soave-Redlich-Kwong
        • 1.3.1.3 Peng-Robinson
  • 1.4 Viriaalinen olomuotoyhtälö
  • 1.5 Muut olomuotoyhtälöt
  • 1.6 Kaasuvakion merkinnät
  • 2 Viitteet

    • Kaasun kokoonpuristuvuusarvojen määrittäminen

    Ideaalikaasun laki määritellään seuraavasti:

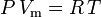
    P\,V_\mathrm{m} = R\,T

    ja epäideaalisuuden suhteen korjattu ideaalikaasun laki määritellään seuraavasti:

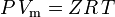
    P\,V_\mathrm{m} = ZR\,T

    missä:
    P = paine
    Vm = kaasun molaarinen tilavuus
    Z = kokoonpuristuvuuskerroin
    R = yleiskaasuvakio
    T = lämpötila

    ja siten:

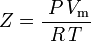
    Z = \frac{\;P\,V_\mathrm{m}}{R\,T}

    , joka on yksinkertaisin ja laajimmin käytetty reaalikaasun olotilayhtälö (EOS). Tämän olotilayhtälön suurin rajoitus on se, että kaasun kokoonpuristuvuustekijä Z ei ole vakio, vaan se vaihtelee kaasusta toiseen sekä tarkasteltavan kaasun lämpötilan ja paineen mukaan. Se on määritettävä kokeellisesti.

    Jos tietyistä kaasuista on saatavilla kokeellista tietoa, sitä voidaan käyttää tuottamaan kuvaajia (kuten kuvassa 1) Z:n ja paineen välisestä riippuvuudesta vakiolämpötilassa tai Z:n ja paineen välisestä riippuvuudesta eri lämpötiloissa kyseisille kaasuille. Tällaisista kuvaajista on hyötyä, kun halutaan helposti saada Z:n interpoloidut arvot kokeellisesti määritettyjen arvojen väliltä.

    Aiemmin mainittu kokoonpuristuvuuskerroin voidaan ilmaista myös seuraavasti:

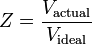
    Z = \frac{V_\mathrm{todellinen}}{V_\mathrm{ideaalinen}}

    Kokoonpuristuvuuskerroin vaikuttaa kolmella tavalla:

    1. Z:n arvo pyrkii kohti 1:tä, kun kaasun paine lähestyy 0:ta, jolloin kaikki kaasut pyrkivät kohti ideaalista käyttäytymistä
    2. Z:n arvo on pienempi kuin 1 välipaineissa, koska molekyylien väliset vetovoimat aiheuttavat sen, että todelliset tilavuudet ovat pienempiä kuin ideaaliset arvot
    3. Z:n arvo on suurempi kuin 1 ja pyrkii lopulta kohti ääretöntä. korkeissa paineissa, koska molekyylien väliset repulsiovoimat aiheuttavat sen, että todelliset tilavuudet ovat suurempia kuin ihannearvot

    Yleistetyt kokoonpuristuvuuskertoimen kuvaajat puhtaille kaasuille

    Yksikäsitteinen suhde kokoonpuristuvuuskertoimen ja redusoidun lämpötilan välillä, Tr ja redusoidun paineen, Pr, välinen yhteys tunnistettiin ensimmäisen kerran van der Waalsin toimesta vuonna 1873, ja se tunnetaan nimellä vastaavien tilojen kahden parametrin periaate. Vastaavien tilojen periaate ilmaisee sen yleistyksen, että kaasun ominaisuudet, jotka ovat riippuvaisia molekyylien välisistä voimista, liittyvät kaasun kriittisiin ominaisuuksiin yleispätevällä tavalla. Tämä tarjoaa tärkeimmän perustan molekyylien ominaisuuksien korrelaatioiden kehittämiselle.

    Kaasujen kokoonpuristuvuuden osalta vastaavien tilojen periaate osoittaa, että kaikilla puhtailla kaasuilla, jotka ovat samassa alennetussa lämpötilassa Tr ja samassa alennetussa paineessa Pr, pitäisi olla sama kokoonpuristuvuuskerroin.

    Alennettu lämpötila ja paine määritellään seuraavasti:

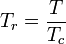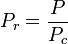
    T_r = \frac{T}{T_c} ja P_r = \frac{P}{P_c}

    Tc ja Pc tunnetaan kaasun kriittisenä lämpötilana ja kriittisenä paineena. Ne ovat kunkin kaasun ominaispiirteitä; Tc on lämpötila, jonka yläpuolella tiettyä kaasua ei ole mahdollista nesteyttää, ja Pc on vähimmäispaine, joka tarvitaan tietyn kaasun nesteyttämiseen sen kriittisessä lämpötilassa. Yhdessä ne määrittelevät nesteen kriittisen pisteen, jonka yläpuolella tietyn nesteen erillisiä neste- ja kaasufaaseja ei esiinny.

    Todellisten kaasujen paine-tilavuus-lämpötila (PVT) -tiedot vaihtelevat puhtaasta kaasusta toiseen. Kun eri yksikomponenttisten kaasujen kokoonpuristuvuuskertoimet esitetään graafisesti paineen funktiona yhdessä lämpötilan isotermien kanssa (kuten metaanin osalta on esitetty kuvan 1 alemmassa kuvaajassa), monilla kuvaajilla on kuitenkin samankaltaiset isotermien muodot.

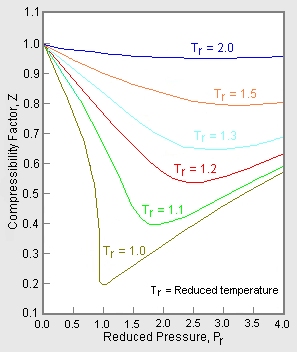
    Kuva 2: Esimerkki yleistetystä kokoonpuristuvuuskertoimen kuvaajasta

    Kaasujen kokoonpuristuvuuskertoimen tietojen normalisoimiseksi käytetään redusoitua painetta ja lämpötilaa, Pr ja Tr, jotta saadaan yleistetty kuvaaja, jota voidaan käyttää monille eri kaasuille. Kuvassa 2 on esimerkki yleistetystä kokoonpuristuvuuskertoimen kuvaajasta, joka on johdettu sadoista kokeellisista P-V-T-tietopisteistä kymmenestä puhtaasta kaasusta, nimittäin metaanista, etaanista, etyleenistä, propaanista, n-butaanista, i-pentaanista, n-heksaanista, typestä, hiilidioksidista ja höyrystä.

    On olemassa yksityiskohtaisempia yleistettyjä kokoonpuristuvuuskertoimen kuvaajia, jotka perustuvat jopa 25 tai useampaan eri puhtaaseen kaasuun, kuten Nelson-Obertin kuvaajat. Tällaisten kuvaajien tarkkuuden sanotaan olevan 1-2 prosentin tarkkuudella, kun Z-arvo on yli 0,6, ja 4-6 prosentin tarkkuudella, kun Z-arvo on 0,3-0,6.

    Yleistetyt kokoonpuristuvuuskertoimen kuvaajat voivat olla huomattavan virheellisiä vahvasti polaarisille kaasuille, jotka ovat kaasuja, joiden positiivisen ja negatiivisen varauksen keskipisteet eivät osu yhteen. Tällaisissa tapauksissa Z:n arvio voi olla jopa 15-20 prosenttia virheellinen.

    Kvanttikaasut vety, helium ja neon eivät noudata vastaavien tilojen käyttäytymistä, ja näiden kolmen kaasun redusoitu paine ja lämpötila olisi määriteltävä uudelleen seuraavalla tavalla, jotta niiden kokoonpuristuvuuskertoimien ennustustarkkuus paranisi, kun käytetään yleistettyjä kuvaajia:

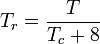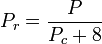
    T_r = \frac{T}{T_c + 8} ja P_r = \frac{P}{P_c + 8}

    missä lämpötilat ovat kelvinasteina ja paineet ilmakehinä.

    Kaasuseosten yleistetyt kokoonpuristuvuuskertoimen kuvaajat

    Puhtaiden kaasujen yleistettyjä kokoonpuristuvuuskertoimen kuvaajia (kuten esimerkiksi kuvassa 2 tai Nelson-Obertin kuvaajissa) voidaan käyttää myös kaasuseosten kuvaajina käyttämällä W. B. Kayn vuonna 1936 ehdottamaa Kayn sääntöä. Tämä sääntö ennustaa kaasuseoksen P-V-T-käyttäytymistä määrittämällä kaasuseoksen kokoonpuristuvuuskerroin alennetussa lämpötilassa ja alennetussa paineessa, jotka määritellään pseudokriittisen lämpötilan Tpc ja pseudokriittisen paineen Ppc avulla, jotka määritellään seuraavasti:

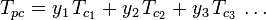
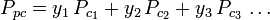
    T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_2} + y_3\,T_{c_3}\,\dots P_{pc} = y_1\,P_{c_1} + y_2\,P_{c_2} + y_3\,P_{c_3}\,\dots

    .

    missä:
    Tpc = kaasuseoksen pseudokriittinen lämpötila
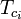    T_{c_i} = kaasuseoksen komponentin kriittinen lämpötila
    Ppc = kaasuseoksen pseudokriittinen lämpötila. kaasuseoksen paine
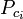    P_{c_i} = kaasun komponentin kriittinen lämpötila
    yi = kaasun komponentin mooli- (tai tilavuus-) osuus

    Pseudoredusoitu lämpötila, Tpr, ja pseudoredusoitu paine, Ppr, joita voidaan käyttää puhtaiden kaasujen yleistettyjen kokoonpuristuvuuskertoimien kuvaajien kanssa, ovat:

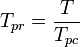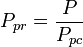
    T_{pr} = \frac{T}{T_{pc}} ja P_{pr} = \frac{P}{P_{pc}}

    Maakaasun (joka on hiilivetyjen ja muiden kaasujen seos) kokoonpuristuvuuskertoimen kuvaaja, jossa käytetään pseudoredusoituja lämpötiloja ja paineita, on saatavissa internetistä.

    Van der Waalsin yhtälö

    Van der Waalsin yhtälö kehitettiin vuonna 1873 ja se voidaan ilmaista seuraavasti:

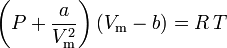
    \left(P + \frac{a}{V_\mathrm{m}^2}\right)\left(V_\mathrm{m} - b\right) = R\,T

    joissa:

    a on kaasumolekyylien välisen vetovoiman voimakkuuden mitta b ottaa huomioon kaasumolekyylien miehittämän tilavuuden, joka pienentää käytettävissä olevaa avointa tilavuutta

    Van der Waalsin yhtälö voidaan järjestää uudelleen seuraavasti:

    a on kaasumolekyylien välisen vetovoiman voimakkuuden mitta:

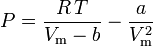
    P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}

    ja kokoonpuristuvuuskerroin voidaan kirjoittaa seuraavasti:

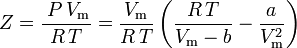
    Z = \frac{\;P\,V_\mathrm{m}}{R\,T} = \frac{V_\mathrm{m}}{R\,T}\left(\frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2}\right)

    ja meillä on nyt yhtälö Z:n määrittämiseksi van der Waalsin parametrien a ja b avulla:

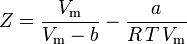
    Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}

    Vaikka a:sta ja b:stä käytetään nimitystä ”Van der Waalsin vakiot”, ne eivät ole todellisia vakioita, koska ne vaihtelevat kaasusta toiseen; ne ovat kuitenkin riippumattomia P:stä, V:sta ja T:stä. Toisin sanoen ne ovat vakioita tarkasteltavana olevalle kaasulle. Kun tiedetään tietyn kaasun kriittinen lämpötila ja paine, a ja b saadaan kyseiselle kaasulle näistä yhtälöistä:

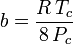
    a = \frac{27\, R^2\, T_c^2}{64\, P_c} ja b = \frac{R\, T_c}{8\, P_c}

    Vaikkapa etaanin kriittinen paine on 4.884 MPa ja kriittinen lämpötila on 305,43 K (32,3˚C). Käyttämällä yleiskaasuvakiota R, joka on 8,3145 Pa m3 K-1 mol-1, saadaan edellä esitetyistä yhtälöistä a = 0,557 m6 Pa mol-2 ja b = 6,500×10-5 m3 mol-1.

    Taulukoituja a:n ja b:n arvoja eri kaasuille on saatavissa näistä viitteistä sekä monista muista lähteistä teknisessä kirjallisuudessa.

    Van der Waalsin yhtälön modifioidut versiot

    Kokoonpuristuvuuskertoimien määrittäminen van der Waalsin tilayhtälön avulla on parannus verrattuna yleistettyjen kokoonpuristuvuustaulukoiden käyttöön. Van der Waalsin olomuodon yhtälöstä on kuitenkin olemassa muunnettuja versioita, jotka parantavat tilannetta entisestään. Öljynjalostuksen, petrokemian tuotannon, maakaasun käsittelyn, kryogeenisen tislauksen ja niihin liittyvien teollisuudenalojen parissa työskentelevien insinöörien ehkä yleisimmin käyttämät olomuotoyhtälöt ovat seuraavat: vuonna 1949 kehitetty Redlichin ja Kwongin yhtälö, vuonna 1972 kehitetty Soaven ja Redlichin ja Kwongin yhtälö sekä vuonna 1976 kehitetty Pengin ja Robinsonin yhtälö. Nämä kolme yhtälöä ovat pääasiassa muunnettuja versioita van der Waalsin yhtälöstä. Vertailuyhtälöt ovat:

    Redlich-Kwong

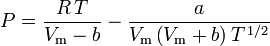
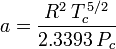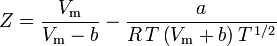
    P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)T^{\,1/2}}} a = \frac{R^2\, T_c^{\,5/2}}{2.3393\, P_c} ja b = \frac{R\, T_c}{11.5420\, P_c} Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{\,1/2}}

    Soave-Redlich-Kwong

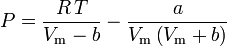
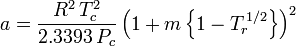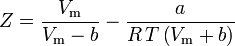
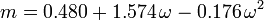
    P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\vasemmalle(V_\mathrm {m} + b\oikealle)} a = \frac{R^2\,T_c^2}{2.3393\,P_c}\, \Big(1 + m\, \Big\{1 - T_r^{\,1/2} \Big\} \Big)^2 ja b = \frac{R\, T_c}{11.5420\, P_c} Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)} m = 0.480 + 1.574\, \omega - 0.176\, \omega^2

    Soave-Redlich-Kwongin ja Peng-Robinsonin yhtälöissä parametrina käytetyn akentrisen tekijän ω esittivät ensimmäisen kerran Pitzer et al. vuonna 1955. Se voidaan ilmaista seuraavasti:

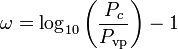
    \omega = \log_{10} \left(\frac{P_c}{P_\mathrm{vp}}\right) - 1

    joissa Pvp on kaasun kyllästetty höyrynpaine lämpötilassa 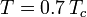T = 0,7\, T_c.

    Peng-Robinson

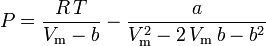
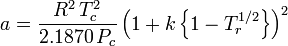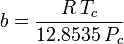
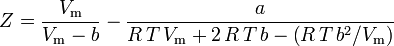
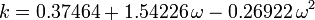
    P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}\, b - b^2} a = \frac{R^2\,T_c^2}{2.1870\,P_c}\, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big)^2 ja b = \frac{R\, T_c}{12.8535\, P_c} Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m} + 2\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)} k = 0,37464 + 1,54226\, \omega - 0,26922\, \omega^2

    Viriaalinen olomuotoyhtälö

    Fundamentaalisin olomuotoyhtälö , sikäli, että sillä on vankimmat teoreettiset perusteet, on viriaalinen olomuotoyhtälö:

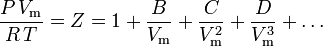
    \frac{P\,V_\mathrm{m}}{R\,T} = Z = 1 + \frac{B}{V_\mathrm{m}} + \frac{C}{V_\mathrm{m}^2} + \frac{D}{V_\mathrm{m}^3} + \dots

    Sen ehdotti ensimmäisen kerran empiiriseltä pohjalta Thiesen vuonna 1885 ja Kamerlingh-Onnes kehitti sitä edelleen vuonna 1901. Tilastollis-mekaanisen lausekkeen B:lle johti ensimmäisenä Ornstein väitöskirjassaan. Myöhemmin H.D. Ursell kehitti yhtälön uudelleen vuonna 1927 molekyylien välisten voimien tilastollis-mekaanisesta (klusterianalyysistä) johdetun teoreettisen perustan pohjalta.

    Parametreihin B, C ja D viitataan vastaavasti toisena, kolmantena ja neljäntenä viriaalikertoimena. Kertoimet eivät ole vakioita, sillä ne vaihtelevat kaasusta toiseen sekä tarkasteltavan kaasun lämpötilan mukaan. Ne kirjoitetaan joskus B(T), C(T) ja D(T) merkiksi siitä, että ne ovat lämpötilan funktioita. Kertoimien numeerinen arvo on määritettävä kokeellisesti.

    Toisen viriaalikertoimen avulla saadaan suurin osa kaasun epäideaalisen käyttäytymisen korjauksesta. Tästä syystä viriaaliyhtälö katkaistaan joskus toisen kertoimen sisältävän termin jälkeen. Kun kolmas kerroin on käytettävissä, yhtälö kuitenkin yleensä katkaistaan kolmannen kertoimen sisältävän termin jälkeen. Neljäs kerroin on harvoin saatavilla.

    Laaja kooste puhtaiden kaasujen ja kaasuseosten viriaalikertoimista laadittiin termodynamiikan tutkimuskeskuksen (Thermodynamics Research Center) viriaalikertoimia koskevasta tietokannasta, joka sijaitsi aiemmin Texas A&M -yliopistossa, College Stationissa, Teksasissa, ja nykyisin kansallisessa standardointi- ja teknologiainstituutissa (National Institute of Standards and Technology, NIST), Boulderissa, Coloradossa. Viimeisin versio tästä koosteesta julkaistiin vuonna 2003. NIST tarjoaa myös ostettavaksi ohjelmiston, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), joka sisältää toisen ja kolmannen viriaalikertoimen sekä lukuisia muita termodynaamisia ominaisuuksia.

    Muut olomuotoyhtälöt

    On olemassa useita muitakin olomuotoyhtälöitä, joilla voidaan ennustaa todellisten kaasujen käyttäytymistä. Ehkä tunnetuimpia ovat vuonna 1929 kehitetty Beattie-Bridgemanin yhtälö ja vuonna 1940 kehitetty Benedict-Rubin-Webbin yhtälö. Yleensä ne ovat monimutkaisempia kuin edellä käsitellyt yhtälöt.

    Kaasuvakion merkintätapa

    Tässä artikkelissa käytetty kaasuvakio on universaali kaasuvakio R, joka pätee kaikkiin kaasuihin. On olemassa myös spesifinen kaasuvakio, jota voidaan merkitä Rs:llä ja joka määritellään seuraavasti: Rs = R / M missä M on molekyylipaino.

    Valitettavasti monet kirjoittajat teknisessä kirjallisuudessa käyttävät toisinaan R:ää ominaiskaasuvakiona ilman, että sitä nimetään sellaiseksi tai ilmoitetaan, että se on ominaiskaasuvakio. Tämä voi johtaa ja johtaakin sekaannuksiin.

    1. 1,0 1,1 1,2 1,3 1,4 McQuarrie, Donald A. ja Simon, John D. (1999). Molecular Thermodynamics. University Science Books. ISBN 1-891389-05-X.
    2. 2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal ja Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, 2. painos. McGraw-Hill Professional. ISBN 0-07-245426-1.
    3. 3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Introduction to Chemical Engineering Thermodynamics, seitsemäs painos. McGraw Hill. ISBN 0-07-310445-0.
    4. 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Kemiantekniikan termodynamiikka. Universities Press (Intia). ISBN 81-7371-048-1.
    5. 5.0 5.1 Kaasulait (Professori M.J. Mombourquetten luento Queensin yliopistossa Kanadassa)
    6. Hong Wei Xiang (2005). Vastaavien tilojen periaate ja sen käytäntö: Thermodynamic, Transport and Surface Properties of Fluids. Elsevier. ISBN 0-444-52062-7.
    7. IUPAC Goldbook
    8. Gouq-Jen Su (1946). ”Modifioitu vastaavien tilojen laki”. Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.
    9. 9.0 9.1 Olomuodon yhtälöt (Professori Lyes Kadem, Concordian yliopisto, Kanada)
    10. 10.0 10.1 Olomuodon yhtälöt (Professori Sanford Kleinin käyttämä luentomateriaali Wisconsin-Madisonin yliopistossa, Yhdysvallat)
    11. Richard W. Miller (1996). Virtausmittaustekniikan käsikirja, 3. painos. McGraw-Hill. ISBN 0-07-042366-0. (Katso kuva G-1 sivulla G.145)
    12. Kai-Fui Vincent Wong (2000). Thermodynamics for Engineers, 1. painos. CRC Press. ISBN 0-8493-0232-3. (Ks. kuva A-2, sivu 278}
    13. Nelson-Obertin yleistetyt kokoonpuristuvuuskaaviot (Kaaviot saatavissa Internetistä, San Diegon valtionyliopiston verkkosivuilta, Yhdysvallat)
    14. W.B.Kay (1936). ”Gases and Vapors At High Temperature and Pressure – Density of Hydrocarbon”. Industrial Engineering & Chemistry 28:1014. ISSN 0096-4484.
    15. Yunus A. Çengal ja Michael A. Bowes (2005). Termodynamiikka: An Engineering Approach, 5. painos. McGraw-Hill. ISBN 0-07-2884959.
    16. Todelliset kaasut (Professori R.M. Pricen käyttämä luentomateriaali Christian Brothers University, U.S.A.)
    17. Luonnonkaasujen ominaisuudet (Professori Jon Steiner Gudmandsson, Norjan tiede- ja teknologiayliopisto)
    18. Robert C. Weast (Toimittaja) (1975). Kemian ja fysiikan käsikirja, 56. painos. CRC Press. ISBN 0-87819-455-X.
    19. 19.0 19.1 19.2 Chapter 3: Equations of State (pages 6-8 of 65 pdf pages) (Osa Ji Lin Wangin väitöskirjasta, 2002, Swinbourne University of Technology, Australia)
    20. 20.0 20.1 20.2 Jean Vidal (2003). Termodynamiikka: Sovellukset kemiantekniikassa ja öljyteollisuudessa. Editions Technip. ISBN 2-7108-0800-5.
    21. Zakia Nasri ja Housam Binous (2007). ”Soave-Redlich-Kwongin tilayhtälön sovellukset Mathematican avulla”. Journal of Chemical Engineering of Japan 40 (6): 534-538. Haettu täältä.
    22. K.S. Pitzer et al (1955). ”The Volumetric and Thermodynamic Properties of Fluids”. Journal of the American Chemical Society 77: 3427-3440.
    23. Francis S. Manning ja Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
    24. Acentric Factor Definition (Physical Property Sources Index, PPSI, of the Swiss Federal Institute of Technology Zurich)
    25. Max F. Thiesen (1885). ”Investigations of the Equation of State”. Annalen der Physik und Chemie (24): 467-492.
    26. Heike Kamerlingh-Onnes (1901). ”Kaasujen ja nesteiden olotilayhtälön ilmaiseminen sarjojen avulla”. Commun. Phys. Lab. Leiden (71).
    27. S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Gibbsin tilastollisen mekaniikan soveltaminen molekyyliteoreettisiin ongelmiin), Leiden
    28. H. D. Ursell (1927). ”The Evaluation of Gibbs’ Phase Integral for Imperfect Gases” (23): 685.
    29. J.D. Dymond ja R.C. Wilhoit (Kirjoittajat), K.N. Marsch ja M. Fenkel (Toimittajat) (2003). Virial Coefficients of Pure gases and Mixtures, 1. painos. Springer. ISBN 3-540-44340-1.
    30. NIST Standard Reference Database 23
    31. J.A. Beattie ja O.C. Bridgeman (1929). ”A New Equation of State for Fluids”. Proc. Amer. Acad. Arts Sci. (63): 229-305.
    32. M. Benedict, G.B. Webb ja L.C. Rubin (1940). ”An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures”. J. Chem. Phys. 8: 334-335.
    Information.svg Osa tämän sivun sisällöstä on saattanut aiemmin ilmestyä Citizendiumissa.
    Haettu osoitteesta ”http://knowino.org/wiki/Compressibility_factor_(gases)”
    Luokka: http://knowino.org/wiki/Compressibility_factor_(gases)
    : Luokka: Fysiikka

    Jätä kommentti