Soluautomaatti on kokoelma ”värillisiä” soluja tietyn muotoisella ruudukolla, joka kehittyy useiden diskreettien aika-askeleiden kautta naapurisolujen tiloihin perustuvien sääntöjen mukaisesti. Sääntöjä sovelletaan sitten iteratiivisesti niin monen aika-askeleen ajan kuin halutaan. von Neumann oli yksi ensimmäisistä, jotka pohtivat tällaista mallia, ja hän sisällytti solumallin ”universaalikonstruktoriinsa”. Soluautomaatteja tutkittiin 1950-luvun alussa biologisten järjestelmien mahdollisena mallina (Wolfram 2002, s. 48). Kattavia tutkimuksia soluautomaateista on tehnyt S. Wolfram 1980-luvulta alkaen, ja Wolframin perustutkimus alalla huipentui hänen julkaisemaansa kirjaan A New Kind of Science (Wolfram 2002), jossa Wolfram esittelee jättimäisen kokoelman automaatteja koskevia tuloksia, joiden joukossa on useita uraauurtavia uusia löytöjä.
Televisiorikosdraaman NUMB3RS 2. kauden jaksossa ”Bettor or Worse” (2006) mainitaan yksiulotteiset soluautomaatit.
Soluautomaatteja on monenlaisia. Yksi soluautomaatin perustavanlaatuisimmista ominaisuuksista on se, minkälaiselle ruudukolle se lasketaan. Yksinkertaisin tällainen ”ruudukko” on yksiulotteinen viiva. Kaksiulotteisissa automaateissa voidaan käyttää neliö-, kolmi- ja kuusikulmaisia ristikoita. Soluautomaatteja voidaan rakentaa myös karteesisille ruuduille mielivaltaisella määrällä ulottuvuuksia, joista 
-ulotteinen kokonaislukuristikko 
on yleisin valinta. Soluautomaatit 
-ulotteisella kokonaislukuhyllyllä toteutetaan Wolfram-kielessä nimellä CellularAutomaton.
Värien (tai erillisten tilojen) 
määrä, jonka soluautomaatti voi ottaa, on myös määritettävä. Tämä luku on tyypillisesti kokonaisluku, ja 
(binäärinen) on yksinkertaisin valinta. Binäärisessä automaatissa väriä 0 kutsutaan yleisesti ”valkoiseksi” ja väriä 1 kutsutaan yleisesti ”mustaksi”. Voidaan kuitenkin harkita myös soluautomaatteja, joilla on jatkuva mahdollisten arvojen alue.
Sen lisäksi, missä ruudukossa soluautomaatti elää ja mitä värejä sen solut voivat ottaa, on määriteltävä myös naapurusto, jonka alueella solut vaikuttavat toisiinsa. Yksinkertaisin valinta on ”lähimmät naapurit”, jossa vain tietyn solun suoraan viereisiin soluihin voidaan vaikuttaa kullakin aika-askeleella. Kaksi yleistä naapurustoa neliöruudukon kaksiulotteisen soluautomaatin tapauksessa ovat niin sanottu Mooren naapurusto (neliönmuotoinen naapurusto) ja von Neumannin naapurusto (vinoneliönmuotoinen naapurusto).
Yksinkertaisin soluautomaattityyppi on kaksiulotteinen, lähimmän naapurin, yksiulotteinen automaatti. Tällaisia automaatteja S. Wolfram kutsui ”elementaarisoluautomaateiksi”, ja hän on tutkinut laajasti niiden hämmästyttäviä ominaisuuksia (Wolfram 1983; 2002, s. 57). Tällaisia automaatteja on 256, ja kutakin niistä voidaan indeksoida yksilöllisellä binääriluvulla, jonka desimaaliesitys tunnetaan kyseisen automaatin ”sääntönä”. Yllä on havainnollistettu sääntöä 30 yhdessä sen tuottaman evoluution kanssa 15 askeleen jälkeen alkaen yhdestä mustasta solusta.
Hieman monimutkaisempi soluautomaattiluokka ovat lähimmän naapurin, 
-väriset, yksiulotteiset totalistiset soluautomaatit. Tällaisissa automaateissa vierekkäisten solujen keskiarvo määrää kehityksen, ja yksinkertaisimmilla ei-triviaaleilla esimerkeillä on 
väriä. Näille automaateille käyttäytymistä kuvaava sääntöjoukko voidaan koodata 
-numeroisena 
-alkuisena lukuna, jota kutsutaan ”koodiksi”. Yllä on esitetty ternaarisen (
) koodin 912 automaatin säännöt ja 300 askelta.
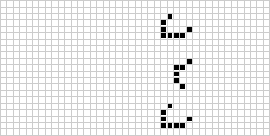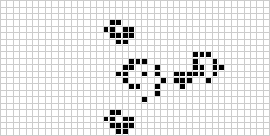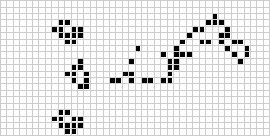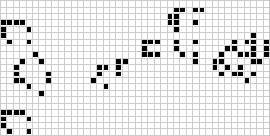
Kahdessa ulottuvuudessa tunnetuin soluautomaatti on J. H. Conwayn vuonna 1970 keksimä Conway’s game of life (Conwayn elämyspeli), jonka Martin Gardner teki tunnetuksi Scientific Americanin kolumneissa. Elämänpeli on binäärinen (
) totalistinen soluautomaatti, jonka Mooren naapurusto on alueella 
. Vaikka peräkkäisten elämänpelisukupolvien laskeminen tehtiin alun perin käsin, tietokonevallankumous saapui pian ja mahdollisti laajempien mallien tutkimisen ja levittämisen. Yllä on havainnollistettu animaatio elämänpelin rakenteesta, joka tunnetaan nimellä puffer train.
WireWorld on toinen yleinen kaksiulotteinen soluautomaatti.
Soluautomaattien teoria on äärettömän rikas, sillä yksinkertaiset säännöt ja rakenteet kykenevät tuottamaan suuren määrän erilaisia odottamattomia käyttäytymismalleja. On esimerkiksi olemassa universaaleja soluautomaatteja, jotka pystyvät simuloimaan minkä tahansa muun soluautomaatin tai Turingin koneen käyttäytymistä. Gacs (2001) on jopa todistanut, että on olemassa vikasietoisia universaaleja soluautomaatteja, joiden kykyä simuloida muita soluautomaatteja eivät estä satunnaiset häiriöt, edellyttäen, että tällaiset häiriöt ovat riittävän harvoja.