Sekoitusmatriisi on taulukko, jota käytetään usein kuvaamaan luokittelumallin (tai ”luokittelijan”) suorituskykyä testidatan joukossa, jonka todelliset arvot tunnetaan. Itse sekoitusmatriisi on suhteellisen helppo ymmärtää, mutta siihen liittyvä terminologia voi olla hämmentävää.
Haluin luoda ”pikaoppaan” sekoitusmatriisiterminologiasta, koska en löytänyt olemassa olevaa resurssia, joka olisi vastannut vaatimuksiani: tiivis esitystapa, numeroiden käyttäminen mielivaltaisten muuttujien sijasta ja selitys sekä kaavojen että lauseiden muodossa.
Aloitetaan esimerkki sekoitusmatriisista binääriluokittelijalle (vaikka sitä voidaan helposti laajentaa useamman kuin kahden luokan tapaukseen):
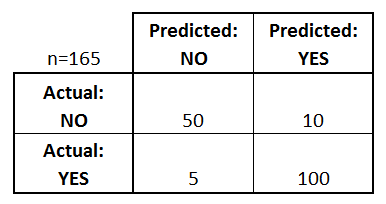
Mitä voimme oppia tästä matriisista?
- On kaksi mahdollista ennustettua luokkaa: ”kyllä” ja ”ei”. Jos ennustaisimme esimerkiksi jonkin sairauden esiintymistä, ”kyllä” tarkoittaisi, että heillä on sairaus, ja ”ei” tarkoittaisi, että heillä ei ole sairautta.
- Luokittelija teki yhteensä 165 ennustetta (esim, 165 potilasta testattiin kyseisen taudin esiintymisen varalta).
- Näistä 165 tapauksesta luokittelija ennusti ”kyllä” 110 kertaa ja ”ei” 55 kertaa.
- Todellisuudessa otoksessa 105 potilaalla on tauti ja 60 potilaalla ei.
Määritellään seuraavaksi perustavanlaatuisimmat termit, jotka ovat kokonaislukuja (eivät prosenttilukuja):
- todelliset positiiviset (true positive) (TP): Nämä ovat tapauksia, joissa ennustimme kyllä (heillä on tauti), ja heillä on tauti.
- true negatives (TN): Ennustimme ei, ja heillä ei ole tautia.
- vääriä positiivisia (FP): Ennustimme kyllä, mutta heillä ei todellisuudessa ole tautia. (Tunnetaan myös nimellä ”tyypin I virhe”.)
- väärät negatiiviset (FN): Ennustimme ei, mutta heillä todella on tauti. (Tunnetaan myös nimellä ”tyypin II virhe”.)
Olen lisännyt nämä termit sekoitusmatriisiin ja lisännyt myös rivien ja sarakkeiden summat:
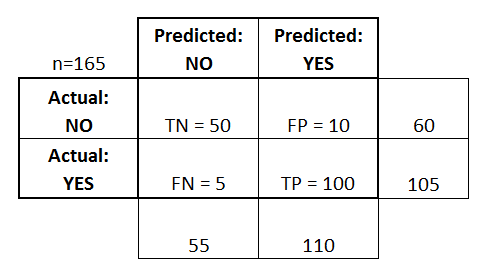
Tässä on luettelo luvuista, jotka usein lasketaan binääriluokittimen sekoitusmatriisista:
- Tarkkuus: Kuinka usein luokittelija on kaiken kaikkiaan oikeassa?
- (TP+TN)/kokonais = (100+50)/165 = 0.91
- Vääräluokitusaste: Kaiken kaikkiaan, kuinka usein se on väärässä?
- (FP+FN)/yhteensä = (10+5)/165 = 0.09
- vastaa 1 miinus Tarkkuus
- tunnetaan myös nimellä ”Virheprosentti”
- Tosi Positiivisten osuus:
- TP/todellinen kyllä = 100/105 = 0.95
- tunnetaan myös nimellä ”Sensitiivisyys” tai ”Recall”
- False Positive Rate:
- FP/todellinen ei = 10/60 = 0.17
- True Negative Rate: Kun se on oikeasti ei, kuinka usein se ennustaa ei?
- TN/todellinen ei = 50/60 = 0.83
- vastaa 1 miinus False Positive Rate
- tunnetaan myös nimellä ”Spesifisyys”
- Tarkkuus: Kun se ennustaa kyllä, kuinka usein se on oikeassa?
- TP/ennustettu kyllä = 100/110 = 0.91
- Yleisyys: Kuinka usein kyllä-ehto todella esiintyy otoksessamme?
- todellinen kyllä/kokonaismäärä = 105/165 = 0.64
Pari muutakin termiä on mainitsemisen arvoinen:
- Nollavirheaste: Tämä kertoo, kuinka usein olisit väärässä, jos ennustaisit aina enemmistöluokan. (Esimerkissämme nollavirheprosentti olisi 60/165=0,36, koska jos ennustaisit aina kyllä, olisit väärässä vain 60 ”ei”-tapauksessa). Tämä voi olla hyödyllinen perusmittari, johon luokittimesi voi verrata. Parhaalla luokittimella tietylle sovellukselle on kuitenkin joskus suurempi virheprosentti kuin nollavirheprosentti, kuten tarkkuusparadoksi osoittaa.
- Cohenin Kappa: Tämä on lähinnä mittari, jolla mitataan, kuinka hyvin luokittimen tulos oli verrattuna siihen, kuinka hyvin se olisi toiminut pelkän sattuman perusteella. Toisin sanoen mallilla on korkea Kappa-pistemäärä, jos tarkkuuden ja nollavirheprosentin välillä on suuri ero. (Lisätietoja Cohenin Kappasta.)
- F-pisteet: Tämä on todellisen positiivisuuden (recall) ja tarkkuuden painotettu keskiarvo. (Lisätietoja F-arvosta.)
- ROC-käyrä: Tämä on yleisesti käytetty kuvaaja, joka tiivistää luokittelijan suorituskyvyn kaikilla mahdollisilla kynnysarvoilla. Se luodaan piirtämällä True Positive Rate (y-akseli) vastaan False Positive Rate (x-akseli), kun vaihdellaan kynnysarvoa, jolla havainnot luokitellaan tiettyyn luokkaan. (Lisätietoja ROC-käyristä.)
Ja lopuksi, niille, jotka ovat Bayesin tilastojen maailmasta, tässä lyhyt yhteenveto näistä termeistä Applied Predictive Modeling -teoksesta:
Suhteessa Bayesin tilastoihin herkkyys ja spesifisyys ovat ehdollisia todennäköisyyksiä, prevalenssi on prior, ja positiiviset/negatiiviset ennustetut arvot ovat posteriorisia todennäköisyyksiä.
Haluatko oppia lisää?
Uudessa 35-minuuttisessa videossani Making sense of the confusion matrix selitän näitä käsitteitä syvällisemmin ja käsittelen edistyneempiä aiheita:
- Miten lasketaan tarkkuus ja palautus usean luokan ongelmille
- Miten analysoidaan 10 luokan sekoitusmatriisia
- Miten valitaan oikea arviointimittari ongelmaasi
- Miten tarkkuus on usein harhaanjohtava mittari
Kertokaa, jos teillä on kysyttävää!