Un automate cellulaire est une collection de cellules « colorées » sur une grille de forme spécifiée qui évolue à travers un certain nombre de pas de temps discrets selon un ensemble de règles basées sur les états des cellules voisines. Les règles sont ensuite appliquées de manière itérative pour autant de pas de temps que souhaité. von Neumann a été l’une des premières personnes à considérer un tel modèle, et a incorporé un modèle cellulaire dans son « constructeur universel ». Les automates cellulaires ont été étudiés au début des années 1950 comme un modèle possible pour les systèmes biologiques (Wolfram 2002, p. 48). Des études exhaustives des automates cellulaires ont été réalisées par S. Wolfram à partir des années 1980, et les recherches fondamentales de Wolfram dans ce domaine ont abouti à la publication de son livre A New Kind of Science (Wolfram 2002) dans lequel Wolfram présente une gigantesque collection de résultats concernant les automates, parmi lesquels figurent un certain nombre de nouvelles découvertes révolutionnaires.
L’épisode de la saison 2 « Bettor or Worse » (2006) de la série policière télévisée NUMB3RS mentionne des automates cellulaires unidimensionnels.
Les automates cellulaires se présentent sous diverses formes et variétés. L’une des propriétés les plus fondamentales d’un automate cellulaire est le type de grille sur laquelle il est calculé. La plus simple de ces « grilles » est une ligne unidimensionnelle. En deux dimensions, on peut envisager des grilles carrées, triangulaires et hexagonales. Les automates cellulaires peuvent également être construits sur des grilles cartésiennes en nombre arbitraire de dimensions, le treillis d’entiers 
dimensionnel 
étant le choix le plus courant. Les automates cellulaires sur un treillis d’entiers 
-dimensionnels sont implémentés dans le Wolfram Language comme CellularAutomaton.
Le nombre de couleurs (ou d’états distincts) 
qu’un automate cellulaire peut assumer doit également être spécifié. Ce nombre est typiquement un entier, avec 
(binaire) étant le choix le plus simple. Pour un automate binaire, la couleur 0 est communément appelée « blanc », et la couleur 1 est communément appelée « noir ». Cependant, les automates cellulaires ayant une gamme continue de valeurs possibles peuvent également être considérés.
En plus de la grille sur laquelle vit un automate cellulaire et des couleurs que ses cellules peuvent prendre, le voisinage sur lequel les cellules s’affectent entre elles doit également être spécifié. Le choix le plus simple est celui des « plus proches voisins », dans lequel seules les cellules directement adjacentes à une cellule donnée peuvent être affectées à chaque pas de temps. Deux voisinages courants dans le cas d’un automate cellulaire bidimensionnel sur une grille carrée sont le voisinage dit de Moore (un voisinage carré) et le voisinage de von Neumann (un voisinage en forme de losange).
Le type le plus simple d’automate cellulaire est un automate unidimensionnel binaire, à plus proches voisins. De tels automates ont été appelés « automates cellulaires élémentaires » par S. Wolfram, qui a largement étudié leurs étonnantes propriétés (Wolfram 1983 ; 2002, p. 57). Il existe 256 automates de ce type, chacun d’entre eux pouvant être indexé par un nombre binaire unique dont la représentation décimale est appelée « règle » pour cet automate particulier. Une illustration de la règle 30 est présentée ci-dessus ainsi que l’évolution qu’elle produit après 15 étapes à partir d’une seule cellule noire.
Une classe d’automates cellulaires un peu plus compliquée est celle des automates cellulaires totalistes unidimensionnels à voisins les plus proches, 
de couleur. Dans ces automates, c’est la moyenne des cellules adjacentes qui détermine l’évolution, et les exemples non triviaux les plus simples ont 
couleurs. Pour ces automates, l’ensemble des règles décrivant le comportement peut être codé sous la forme d’un nombre 
-chiffre 
-aire appelé « code ». Les règles et les 300 étapes de l’automate ternaire (
) code 912 sont illustrées ci-dessus.
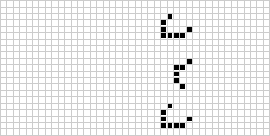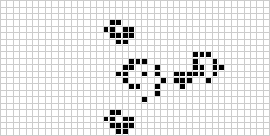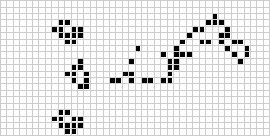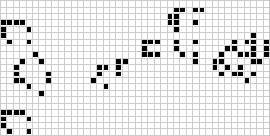
En deux dimensions, l’automate cellulaire le plus connu est le jeu de la vie de Conway, découvert par J. H. Conway en 1970 et popularisé dans les colonnes de Scientific American de Martin Gardner. Le jeu de la vie est un automate cellulaire totaliste binaire (
) avec un voisinage de Moore de portée 
. Bien que le calcul des générations successives du jeu de la vie ait été fait à l’origine à la main, la révolution informatique est arrivée rapidement et a permis d’étudier et de propager des modèles plus étendus. Une animation de la construction du jeu de la vie connue sous le nom de train de puffer est illustrée ci-dessus.
WireWorld est un autre automate cellulaire bidimensionnel commun.
La théorie des automates cellulaires est immensément riche, des règles et des structures simples étant capables de produire une grande variété de comportements inattendus. Par exemple, il existe des automates cellulaires universels qui sont capables de simuler le comportement de n’importe quel autre automate cellulaire ou machine de Turing. Il a même été prouvé par Gacs (2001) qu’il existe des automates cellulaires universels tolérants aux fautes, dont la capacité à simuler d’autres automates cellulaires n’est pas entravée par des perturbations aléatoires, à condition que ces perturbations soient suffisamment éparses.