Biographie

Brahmagupta (598-668 CE)
Le grand mathématicien et astronome indien du VIIe siècle Brahmagupta a écrit des ouvrages importants à la fois sur les mathématiques et l’astronomie. Il était originaire de l’État du Rajasthan, dans le nord-ouest de l’Inde (il est souvent appelé Bhillamalacarya, le professeur de Bhillamala), et devint plus tard le chef de l’observatoire astronomique d’Ujjain, dans le centre de l’Inde. La plupart de ses œuvres sont composées en vers elliptiques, une pratique courante dans les mathématiques indiennes de l’époque, et ont par conséquent quelque chose de poétique.
Il semble probable que les travaux de Brahmagupta, en particulier son texte le plus célèbre, le « Brahmasphutasiddhanta », ont été apportés par le calife abbasside du 8ème siècle Al-Mansur à son centre d’apprentissage nouvellement fondé à Bagdad sur les rives du Tigre, fournissant un lien important entre les mathématiques et l’astronomie indiennes et la recrudescence naissante de la science et des mathématiques dans le monde islamique.
Dans son ouvrage sur l’arithmétique, Brahmagupta explique comment trouver le cube et la racine cubique d’un nombre entier et donne des règles facilitant le calcul des carrés et des racines carrées. Il a également donné des règles pour traiter cinq types de combinaisons de fractions. Il a donné la somme des carrés des n premiers nombres naturels comme n(n + 1)(2n + 1)⁄ 6 et la somme des cubes des n premiers nombres naturels comme (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Traiter le zéro comme un nombre

Les règles de Brahmagupta pour traiter le zéro et les nombres négatifs
Le génie de Brahmagupta, cependant, est venu dans son traitement du concept (alors relativement nouveau) du nombre zéro. Bien que souvent aussi attribué au mathématicien indien du 7ème siècle Bhaskara I, son « Brahmasphutasiddhanta » est probablement le premier texte connu à traiter le zéro comme un nombre à part entière, plutôt que comme un simple chiffre de remplacement comme le faisaient les Babyloniens, ou comme un symbole d’un manque de quantité comme le faisaient les Grecs et les Romains.
Brahmagupta a établi les règles mathématiques de base pour traiter le zéro (1 + 0 = 1 ; 1 – 0 = 1 ; et 1 x 0 = 0), bien que sa compréhension de la division par zéro était incomplète (il pensait que 1 ÷ 0 = 0). Près de 500 ans plus tard, au XIIe siècle, un autre mathématicien indien, Bhaskara II, a montré que la réponse devait être l’infini, et non zéro (au motif que 1 peut être divisé en une infinité de morceaux de taille zéro), une réponse qui a été considérée comme correcte pendant des siècles. Cependant, cette logique n’explique pas pourquoi 2 ÷ 0, 7 ÷ 0, etc, devraient également être zéro – le point de vue moderne est qu’un nombre divisé par zéro est en fait « indéfini » (c’est-à-dire qu’il n’a pas de sens).
La vision de Brahmagupta des nombres en tant qu’entités abstraites, plutôt que simplement pour compter et mesurer, lui a permis de faire encore un autre énorme saut conceptuel qui aurait une profonde conséquence pour les mathématiques futures. Auparavant, la somme 3 – 4, par exemple, était considérée comme dénuée de sens ou, au mieux, comme un simple zéro. Brahmagupta, cependant, s’est rendu compte qu’il pouvait exister une telle chose qu’un nombre négatif, qu’il a appelé « dette » par opposition à « propriété ». Il a exposé les règles pour traiter les nombres négatifs (par exemple, un négatif fois un négatif est un positif, un négatif fois un positif est un négatif, etc.).
En outre, il a souligné que les équations quadratiques (du type x2 + 2 = 11, par exemple) pourraient en théorie avoir deux solutions possibles, dont l’une pourrait être négative, car 32 = 9 et -32 = 9. En plus de ses travaux sur les solutions aux équations linéaires générales et aux équations quadratiques, Brahmagupta est allé encore plus loin en considérant les systèmes d’équations simultanées (ensemble d’équations contenant plusieurs variables), et en résolvant les équations quadratiques à deux inconnues, ce qui n’a même pas été envisagé en Occident jusqu’à mille ans plus tard, lorsque Fermat a considéré des problèmes similaires en 1657.
Le théorème de Brahmagupta sur les quadrilatères cycliques
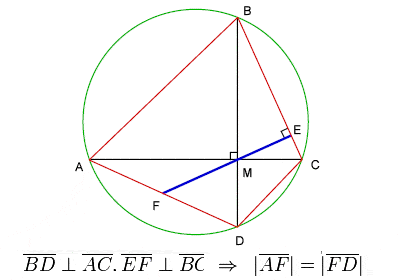
Le théorème de Brahmagupta sur les quadrilatères cycliques
Brahmagupta a même tenté d’écrire ces concepts plutôt abstraits, en utilisant les initiales des noms des couleurs pour représenter les inconnues dans ses équations, l’une des premières intimations de ce que nous connaissons aujourd’hui sous le nom d’algèbre.
Brahmagupta a consacré une partie importante de son œuvre à la géométrie et à la trigonométrie. Il a établi √10 (3,162277) comme une bonne approximation pratique de π (3,141593), et a donné une formule, maintenant connue sous le nom de formule de Brahmagupta, pour l’aire d’un quadrilatère cyclique, ainsi qu’un célèbre théorème sur les diagonales d’un quadrilatère cyclique, généralement appelé théorème de Brahmagupta.
| << Retour aux Mathématiques indiennes | Avantage de Madhava >> |
.