Coordonnées barycentriques

par
Géométrie > Géométrie des coordonnées >
Géométrie > Géométrie plane > Triangles > Propriétés des triangles >

Les coordonnées barycentriques sont des triples de nombres (t_1,t_2,t_3) correspondant à des masses placées aux sommets d’un triangle de référence DeltaA_1A_2A_3. Ces masses déterminent alors un point P, qui est le centroïde géométrique des trois masses et est identifié par les coordonnées (t_1,t_2,t_3). Les sommets du triangle sont donnés par (1,0,0), (0,1,0), et (0,0,1). Les coordonnées barycentriques ont été découvertes par Möbius en 1827 (Coxeter 1969, p. 217 ; Fauvel et al. 1993).

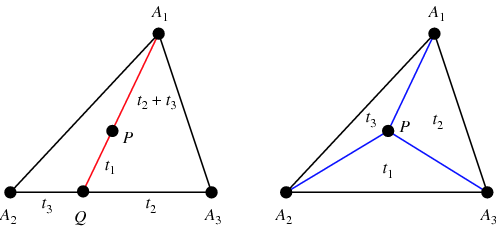
Barycentric

Pour trouver les coordonnées barycentriques d’un point arbitraire P, trouver t_2 et t_3 du point Q à l’intersection de la droite A_1P avec le côté A_2A_3, puis déterminer t_1 comme étant la masse à A_1 qui équilibrera une masse t_2+t_3 à Q, faisant ainsi de P le centroïde (figure de gauche). De plus, les aires des triangles DeltaA_1A_2P, DeltaA_1A_3P, et DeltaA_2A_3P sont proportionnelles aux coordonnées barycentriques t_3, t_2, et t_1 de P (figure de droite ; Coxeter 1969, p. 217).

Les coordonnées barycentriques sont homogènes, donc

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

pour mu !=0.

Les coordonnées barycentriques normalisées pour qu’elles deviennent les aires réelles des soustriangles sont appelées coordonnées barycentriques homogènes. Les coordonnées barycentriques normalisées de sorte que

t_1+t_2+t_3=1,
(2)

de sorte que les coordonnées donnent les aires des soustriangles normalisées par l’aire du triangle initial sont appelées coordonnées aréales (Coxeter 1969, p. 218). Les coordonnées barycentriques et aréales peuvent fournir des preuves particulièrement élégantes de théorèmes géométriques tels que le théorème de Routh, le théorème de Ceva et le théorème de Ménélas (Coxeter 1969, p. 219-221).

(Pas nécessairement homogènes) les coordonnées barycentriques d’un certain nombre de centres communs sont résumées dans le tableau suivant. Dans le tableau, a, b, et c sont les longueurs des côtés du triangle et s est son semi-périmètre.

centre du triangle coordonnées barycentriques
centre de la circonférence O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excentrique J_A (-a,b,c)
excentrique J_B (a,-b,c)
excentrique J_C (a,b,-c)
Point de Gergonne Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
entrée I (a,b,c)
point de Nagel Na (s-a,s-b,s-c)
orthocentre H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
point symétrique K (a^2,b^2,c^2)
centroïde du triangle G (1,1,1)

En coordonnées barycentriques, une droite a une équation linéaire homogène. En particulier, la droite joignant les points (r_1,r_2,r_3) et (s_1,s_2,s_3) a pour équation

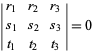|r_1 r_2 r_3 ; s_1 s_2 s_3 ; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 et 57 ; Coxeter 1969, p. 219 ; Bottema 1982). Si les sommets P_i d’un triangle DeltaP_1P_2P_3 ont des coordonnées barycentriques (x_i,y_i,z_i), alors l’aire du triangle est

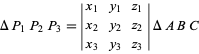DeltaP_1P_2P_3=|x_1 y_1 z_1 ; x_2 y_2 z_2 ; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Laisser un commentaire