Introduction
Les sites actifs d’une enzyme sont généralement composés de résidus d’acides aminés ; selon les résidus d’acides aminés présents, la spécificité du substrat peut varier fortement. En fonction du niveau de pH, les propriétés physiques (principalement la charge électrique) d’une enzyme peuvent changer. Une modification de la charge électrique peut altérer l’interaction entre les résidus d’acides aminés du site actif et le substrat entrant. Cela dit, le substrat peut se lier au site actif par une liaison hydrogène ou des forces de van der Waals. Une fois que le substrat se lie au site actif, il forme un complexe enzyme-substrat qui est ensuite impliqué dans d’autres réactions chimiques.
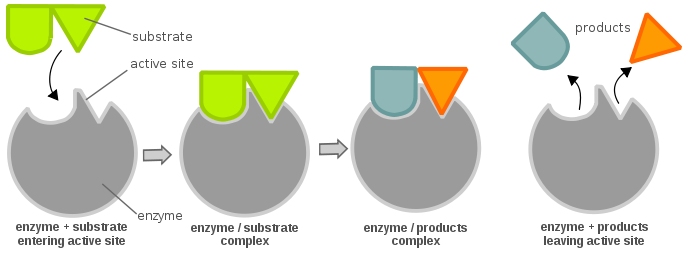
Pour qu’une enzyme soit active et soit énergétiquement favorable pour permettre à une réaction chimique d’avancer, un substrat doit se lier au « site actif » d’une enzyme. Un site actif peut être considéré comme une serrure et le substrat comme une clé ; c’est ce qu’on appelle le modèle de la serrure et de la clé. Une clé (substrat) doit être insérée et tournée (réaction chimique), puis la serrure (enzyme) s’ouvre (production de produits). Notez qu’une enzyme peut avoir plus d’un site actif. Une autre théorie sur la relation site actif-substrat est la théorie de l’ajustement induit, qui est tout à fait opposée à la théorie de la serrure et de la clé (où le site actif est apparemment inflexible). Dans la théorie de l’ajustement induit, le site actif de l’enzyme est très flexible, et ne change de conformation que lorsque le substrat s’y lie.
Les enzymes fonctionnent comme un catalyseur en abaissant l’énergie libre d’activation de Gibbs du complexe enzyme-substrat. Voici deux figures montrant une réaction enzymatique de base avec et sans catalyseur :
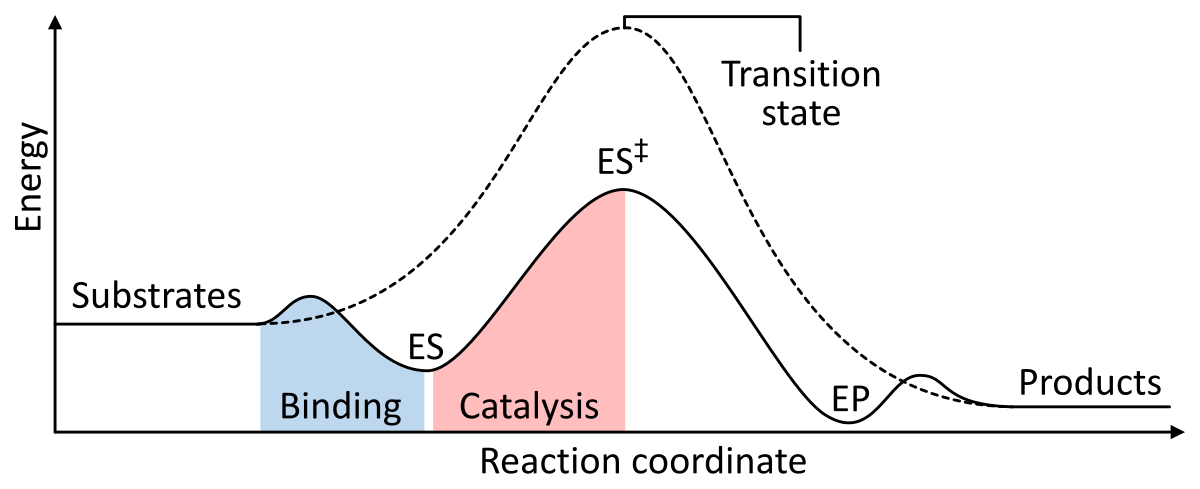
Figure 1 : Les énergies des étapes d’une réaction chimique. Non catalysée (ligne pointillée), les substrats ont besoin de beaucoup d’énergie d’activation pour atteindre un état de transition, qui se désintègre ensuite en produits de plus faible énergie. Lorsqu’elle est catalysée par une enzyme (ligne continue), l’enzyme fixe les substrats (ES), puis stabilise l’état de transition (ES‡) pour réduire l’énergie d’activation nécessaire à la fabrication des produits (EP) qui sont finalement libérés. de Wikipédia.
L’efficacité de l’enzyme peut être déterminée comme suit : considérons une réaction enzymatique simple :
Le biochimiste allemand Leonor Michaelis et la biochimiste canadienne Maud Menten ont dérivé une équation décrivant ce système, connue plus tard sous le nom d' »équation de Michaelis-Menten », présentée ci-dessous :
\}{K_M + }
Cette équation donne la vitesse de la réaction à une concentration de substrat donnée, en supposant une Vmax connue, qui est la vitesse maximale à laquelle la réaction peut se dérouler, et KM, la constante de Michaelis. Cependant, dans une application pratique de l’équation de Michaelis-Menten, V0 est souvent mesuré, et Vmax est observé comme une saturation ou un plateau dans un graphique de données. Comme la concentration du substrat est connue, KM est généralement la valeur calculée d’intérêt.
Pour \(K_M\), supposez \(V_0= \dfrac{V_{max}}{2}\):
\}{K_M + } \tag{2}\]
\) \dfrac{V_{max}}{2} = V_{max} \tag{3}\N
\N = \dfrac{V_{max}}{\dfrac{V_{max}}{2}} \tag{4} \]
\ = 2 \tag{5}\]
\ \tag{6}\]
La constante de Michaelis peut être considérée comme la vitesse à laquelle le substrat se détache de l’enzyme, ce qui peut se produire soit dans les événements du complexe substrat-enzyme devenant le produit, soit le substrat se détache de l’enzyme. KM peut être représenté par une équation.
\
Où k-1 est la constante de vitesse à laquelle le substrat se détache de l’enzyme, ce qui entraîne la dissociation du complexe enzyme-substrat, k2 est la constante de vitesse où le complexe substrat-enzyme disparaît et se transforme en produit, et K1 est la constante de vitesse pour la formation du complexe substrat-enzyme. Par conséquent, le KM peut être considéré comme la vitesse de disparition du complexe substrat-enzyme divisée par la vitesse de formation du complexe substrat-enzyme, qui est le niveau auquel la moitié du substrat est liée à l’enzyme. Le KM est un indicateur utile de la présence d’un inhibiteur car nous pouvons observer les changements de KM et les comparer à notre témoin (systèmes biologiques dont nous savons que la présence d’inhibiteurs est nulle). Le KM est une variable dépendante, et sa valeur peut changer pour de nombreuses raisons, notamment le niveau de pH du système, la température ou toute autre condition susceptible d’affecter une réaction chimique. Un petit KM indique que le substrat a une grande affinité pour l’enzyme.
L’équation de Michaelis-Menten est plus utile pour mesurer l’efficacité de l’enzyme si v0 est tracé en fonction de , comme suit :
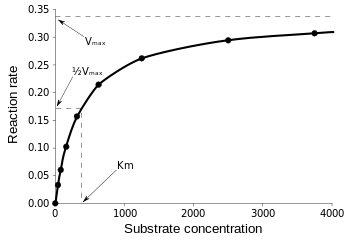
Figure 3 : Schéma de la vitesse de réaction et de la constante de Michaelis-Menten. de Wikipedia.
Vmax est la vitesse maximale à laquelle la réaction peut s’exécuter, indépendamment de , ce qui signifie que même si vous ajoutez plus de substrat, la réaction ne peut pas aller plus vite. Cela est dû au fait qu’à Vmax, tous les sites actifs de l’enzyme sont occupés. Après toutes les explications sur les différentes formes d’équations cinétiques enzymatiques, nous arrivons à notre conclusion sur l’efficacité catalytique. En se référant à la Fig 3, nous avons :
\_o}{\dfrac{k_{-1} + k_2}{k_1} + }\right) \tag{8}\]
Notez que \(k_2\) décrit une réaction irréversible par opposition à une expression d’équilibre, par rapport à k-1 et k1. k2 ici est également connu sous le nom de kcat, l’efficacité catalytique de l’enzyme. D’après la discussion précédente, v0 est la vitesse de réaction mesurée, c’est-à-dire la formation du produit au cours du temps, on peut donc en conclure qu’une équation ressemblerait à ce qui suit :
\}{dt} = k_2_0 \tag{9}\]
Où 0 est la concentration totale en enzyme.
On sait également que la VMax est observée lorsque la totalité du complexe enzyme-substrat disparaît et se transforme en produits, on peut donc faire l’hypothèse suivante :
\_0 \tag{10}\]
. \]
et après réarrangement, nous avons cette équation:
\_0} \tag{11}\]
C’est l’équation pour calculer l’efficacité catalytique, à utiliser après avoir obtenu des données d’expériences et après avoir utilisé l’équation de Michaelis-Menten. Avec un kcat plus grand, l’enzyme est efficace car moins d’enzyme est nécessaire.