Une matrice de confusion est un tableau qui est souvent utilisé pour décrire la performance d’un modèle de classification (ou « classificateur ») sur un ensemble de données de test pour lesquelles les vraies valeurs sont connues. La matrice de confusion elle-même est relativement simple à comprendre, mais la terminologie connexe peut prêter à confusion.
J’ai voulu créer un « guide de référence rapide » pour la terminologie de la matrice de confusion parce que je n’ai pas trouvé de ressource existante qui répondait à mes exigences : présentation compacte, utilisation de nombres au lieu de variables arbitraires, et explication à la fois en termes de formules et de phrases.
Débutons avec un exemple de matrice de confusion pour un classificateur binaire (bien qu’il puisse facilement être étendu au cas de plus de deux classes):
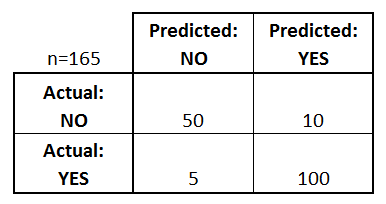
Que pouvons-nous apprendre de cette matrice?
- Il y a deux classes prédites possibles : « oui » et « non ». Si nous prédisions la présence d’une maladie, par exemple, « oui » signifierait qu’ils ont la maladie, et « non » qu’ils ne l’ont pas.
- Le classificateur a fait un total de 165 prédictions (ex, 165 patients étaient testés pour la présence de cette maladie).
- Sur ces 165 cas, le classificateur a prédit « oui » 110 fois, et « non » 55 fois.
- En réalité, 105 patients de l’échantillon ont la maladie, et 60 patients ne l’ont pas.
Définissons maintenant les termes les plus fondamentaux, qui sont des nombres entiers (et non des taux) :
- vrais positifs (TP) : Ce sont les cas dans lesquels nous avons prédit oui (ils ont la maladie), et ils ont effectivement la maladie.
- Vrais négatifs (TN) : Nous avons prédit non, et ils n’ont pas la maladie.
- Faux positifs (FP) : Nous avons prédit oui, mais ils n’ont pas réellement la maladie. (Également appelé « erreur de type I ».)
- faux négatifs (FN) : Nous avons prédit que non, mais ils ont en fait la maladie. (Également connu sous le nom d' » erreur de type II « .)
J’ai ajouté ces termes à la matrice de confusion, et j’ai également ajouté les totaux des lignes et des colonnes :
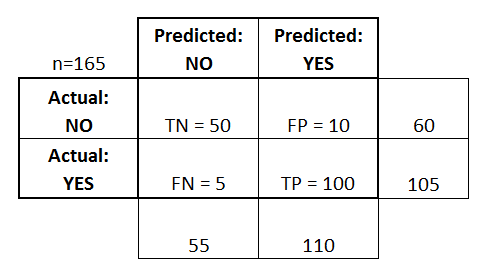
Voici une liste des taux qui sont souvent calculés à partir d’une matrice de confusion pour un classificateur binaire :
- Précision : Globalement, combien de fois le classificateur est-il correct?
- (TP+TN)/total = (100+50)/165 = 0,91
- Taux de mauvaise classification : Dans l’ensemble, combien de fois est-il faux ?
- (FP+FN)/total = (10+5)/165 = 0,09
- équivalent à 1 moins la précision
- également connu sous le nom de « taux d’erreur »
- Taux de vrais positifs : Lorsque c’est réellement oui, combien de fois prédit-il oui ?
- TP/réel oui = 100/105 = 0,95
- également appelé « Sensibilité » ou « Rappel »
- Taux de faux positifs : Lorsqu’il s’agit en réalité d’un non, combien de fois prédit-il un oui ?
- FP/réel non = 10/60 = 0,17
- Taux de vrais négatifs : Lorsqu’il s’agit d’un non réel, combien de fois prédit-il un non ?
- TN/non réel = 50/60 = 0,83
- équivalent à 1 moins le taux de faux positifs
- également appelé « spécificité »
- Précision : Lorsqu’il prédit un oui, combien de fois est-il correct ?
- TP/prédit oui = 100/110 = 0,91
- Prévalence : Combien de fois la condition oui se produit-elle réellement dans notre échantillon ?
- oui réel/total = 105/165 = 0,64
D’autres termes méritent également d’être mentionnés :
- Taux d’erreur nul : Il s’agit de la fréquence à laquelle vous vous tromperiez si vous prédisiez toujours la classe majoritaire. (Dans notre exemple, le taux d’erreur nulle serait de 60/165=0,36 car si vous prédisiez toujours le oui, vous ne vous tromperiez que pour les 60 cas de » non « ). Cela peut être une mesure de base utile pour comparer votre classificateur. Cependant, le meilleur classificateur pour une application particulière aura parfois un taux d’erreur plus élevé que le taux d’erreur nul, comme le démontre le paradoxe de l’exactitude.
- Kappa de Cohen : Il s’agit essentiellement d’une mesure de la performance du classificateur par rapport à la performance qu’il aurait obtenue simplement par hasard. En d’autres termes, un modèle aura un score de Kappa élevé s’il y a une grande différence entre la précision et le taux d’erreur nul. (Plus de détails sur le Kappa de Cohen.)
- Score F : Il s’agit d’une moyenne pondérée du taux de vrais positifs (rappel) et de la précision. (Plus de détails sur le score F.)
- Courbe ROC : C’est un graphique couramment utilisé qui résume la performance d’un classificateur sur tous les seuils possibles. Il est généré en traçant le taux de vrais positifs (axe des y) par rapport au taux de faux positifs (axe des x) lorsque vous faites varier le seuil d’affectation des observations à une classe donnée. (Plus de détails sur les courbes ROC.)
Et enfin, pour ceux d’entre vous qui viennent du monde des statistiques bayésiennes, voici un résumé rapide de ces termes tirés de Applied Predictive Modeling:
En relation avec les statistiques bayésiennes, la sensibilité et la spécificité sont les probabilités conditionnelles, la prévalence est le préalable, et les valeurs prédites positives/négatives sont les probabilités postérieures.
Vous voulez en savoir plus ?
Dans ma nouvelle vidéo de 35 minutes, Making sense of the confusion matrix, j’explique ces concepts plus en profondeur et je couvre des sujets plus avancés :
- Comment calculer la précision et le rappel pour les problèmes multi-classes
- Comment analyser une matrice de confusion à 10 classes
- Comment choisir la bonne métrique d’évaluation pour votre problème
- Pourquoi la précision est souvent une métrique trompeuse
Faites-moi savoir si vous avez des questions !