Objectif d’apprentissage
1. Convertir d’une unité à une autre unité du même type.
Dans la section 2.2 « Exprimer les unités », nous avons montré quelques exemples de remplacement des unités initiales par d’autres unités du même type pour obtenir une valeur numérique plus facile à comprendre. Dans cette section, nous allons formaliser ce processus.
Considérez un exemple simple : combien de pieds y a-t-il dans 4 yards ? La plupart des gens répondront presque automatiquement qu’il y a 12 pieds dans 4 yards. Comment avez-vous fait cette détermination ? Eh bien, s’il y a 3 pieds dans 1 yard et qu’il y a 4 yards, alors il y a 4 × 3 = 12 pieds dans 4 yards.
C’est correct, bien sûr, mais c’est informel. Formalisons-le d’une manière qui puisse être appliquée plus généralement. Nous savons que 1 yard (yd) est égal à 3 pieds (ft) :
1 yd = 3 ft
En mathématiques, cette expression est appelée une égalité. Les règles de l’algèbre disent que vous pouvez modifier (c’est-à-dire multiplier ou diviser ou ajouter ou soustraire) l’égalité (tant que vous ne divisez pas par zéro) et la nouvelle expression sera toujours une égalité. Par exemple, si nous divisons les deux côtés par 2, nous obtenons
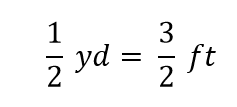
Nous voyons qu’une moitié de yard est égale à 3/2, ou un et demi, pieds-quelque chose que nous savons également être vrai, donc l’équation ci-dessus est toujours une égalité. Pour revenir à l’égalité initiale, supposons que nous divisions les deux côtés de l’équation par 1 yard (nombre et unité):
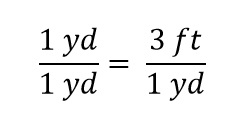
L’expression est toujours une égalité, selon les règles de l’algèbre. La fraction de gauche est égale à 1. Elle a la même quantité au numérateur et au dénominateur, donc elle doit être égale à 1. Les quantités dans le numérateur et le dénominateur s’annulent, à la fois le nombre et l’unité:
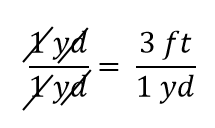
Quand tout s’annule dans une fraction, la fraction se réduit à 1:
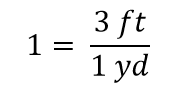
Nous avons une expression, 3 ft1 yd, qui est égale à 1. C’est une façon étrange d’écrire 1, mais c’est logique : 3 ft égalent 1 yd, donc les quantités du numérateur et du dénominateur sont la même quantité, juste exprimée avec des unités différentes. L’expression 3 ft1 yd est appelée facteur de conversion, et elle est utilisée pour changer formellement l’unité d’une quantité en une autre unité. (Le processus de conversion des unités de cette manière formelle est parfois appelé analyse dimensionnelle ou méthode de l’étiquette factorielle.)
Pour voir comment cela se produit, commençons par la quantité originale :
4 yd
Maintenant, multiplions cette quantité par 1. Lorsque vous multipliez quelque chose par 1, vous ne changez pas la valeur de la quantité. Plutôt que de multiplier par 1 seulement, écrivons 1 comme 3 ft1 yd:
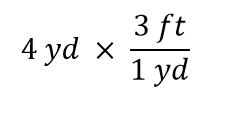
Le terme 4 yd peut être considéré comme 4 yd/1 ; c’est-à-dire qu’il peut être considéré comme une fraction avec 1 au dénominateur. Nous sommes essentiellement en train de multiplier des fractions. Si la même chose apparaît au numérateur et au dénominateur d’une fraction, elles s’annulent. Dans ce cas, ce qui s’annule est l’unité yard:
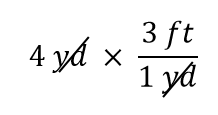
C’est tout ce que nous pouvons annuler. Maintenant, multipliez et divisez tous les nombres pour obtenir la réponse finale :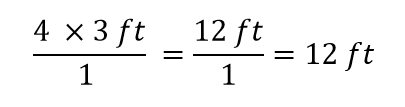
De nouveau, nous obtenons une réponse de 12 pi, tout comme nous l’avons fait à l’origine. Mais dans ce cas, nous avons utilisé une procédure plus formelle qui est applicable à une variété de problèmes.
Combien de millimètres y a-t-il dans 14,66 m ? Pour répondre à cette question, nous devons construire un facteur de conversion entre millimètres et mètres et l’appliquer correctement à la quantité initiale. Nous commençons par la définition d’un millimètre, qui est
1 mm = 1/1 000 m
Le 1/1 000 est ce que signifie le préfixe milli-. La plupart des gens sont plus à l’aise pour travailler sans fractions, nous allons donc réécrire cette équation en amenant le 1 000 dans le numérateur de l’autre côté de l’équation :
1 000 mm = 1 m
Nous construisons maintenant un facteur de conversion en divisant une quantité dans les deux côtés. Mais maintenant une question se pose : par quelle quantité devons-nous diviser ? Il s’avère que nous avons deux choix, et les deux choix nous donneront des facteurs de conversion différents, tous deux égaux à 1:
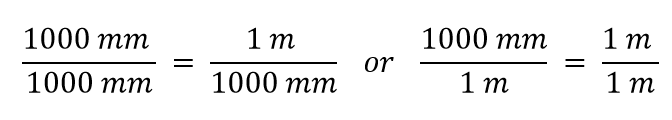
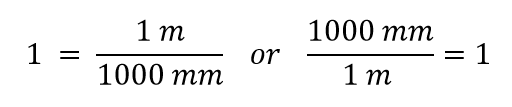
Quel facteur de conversion devons-nous utiliser ? La réponse est basée sur l’unité dont vous voulez vous débarrasser dans votre quantité initiale. L’unité d’origine de notre quantité est le mètre, que nous voulons convertir en millimètres. Comme l’unité d’origine est supposée être au numérateur, pour s’en débarrasser, nous voulons que l’unité de mètre soit au dénominateur ; ils s’annuleront alors. Par conséquent, nous utiliserons le deuxième facteur de conversion. En annulant les unités et en effectuant les mathématiques, nous obtenons
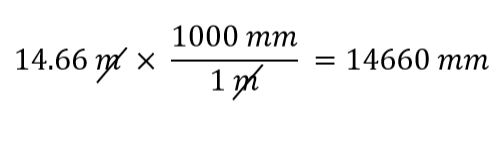
Notez comment m s’annule, laissant mm, qui est l’unité d’intérêt.
La capacité de construire et d’appliquer les facteurs de conversion appropriés est une technique mathématique très puissante en chimie. Vous devez maîtriser cette technique si vous voulez réussir dans ce cours et les suivants.
Exemple 7
- Convertir 35,9 kL en litres.
- Convertir 555 nm en mètres.
Solution
-
Nous allons utiliser le fait que 1 kL = 1 000 L. Parmi les deux facteurs de conversion qui peuvent être définis, celui qui fonctionnera est 1 000 L/1 kL. En appliquant ce facteur de conversion, nous obtenons
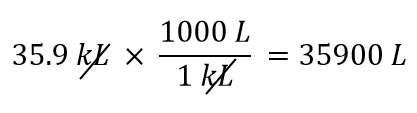
-
Nous allons utiliser le fait que 1 nm = 1/1 000 000 000 m, ce que nous réécrirons comme 1 000 000 000 nm = 1 m, ou 109 nm = 1 m. Des deux facteurs de conversion possibles, celui qui convient a l’unité nm au dénominateur : 1 m/109 nm. En appliquant ce facteur de conversion, nous obtenons
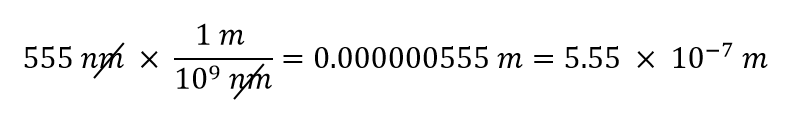
Dans la dernière étape, nous avons exprimé la réponse en notation scientifique.
Testez vous-même
- Convertissez 67.08 μL en litres.
- Convertir 56,8 m en kilomètres.
Réponses
- 6,708 × 10-5 L
- 5,68 × 10-2 km
Qu’en est-il si nous avons une unité dérivée qui est le produit de plus d’une unité, comme le m2 ? Supposons que nous voulions convertir des mètres carrés en centimètres carrés ? La clé est de se rappeler que m2 signifie m × m, ce qui signifie que nous avons deux unités de mètres dans notre unité dérivée. Cela signifie que nous devons inclure deux facteurs de conversion, un pour chaque unité. Par exemple, pour convertir 17,6 m2 en centimètres carrés, nous effectuons la conversion comme suit :
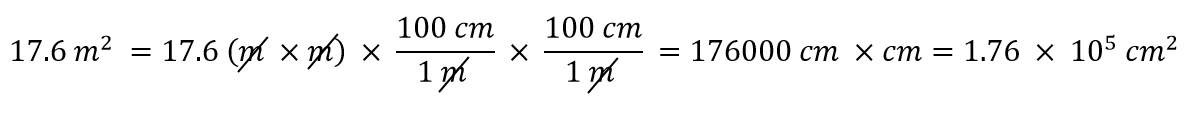
Exemple 8
Combien de centimètres cubes y a-t-il dans 0.883 m3?
Solution
Avec un exposant de 3, nous avons trois unités de longueur, donc par extension nous devons utiliser trois facteurs de conversion entre les mètres et les centimètres. Ainsi, nous avons
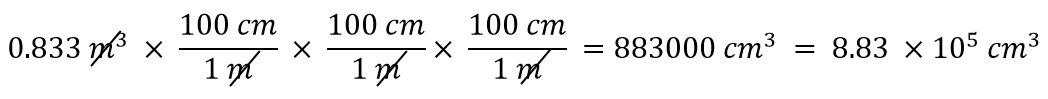
Vous devez vous démontrer que les trois unités de mètres s’annulent effectivement.
Testez vous-même
Combien de millimètres cubes sont présents dans 0,0923 m3 ?
Réponse
9,23 × 107 mm3
Supposons que l’unité que vous voulez convertir se trouve au dénominateur d’une unité dérivée ; que faire alors ? Alors, dans le facteur de conversion, l’unité que vous voulez supprimer doit être au numérateur. Cela annulera l’unité originale dans le dénominateur et introduira une nouvelle unité dans le dénominateur. L’exemple suivant illustre cette situation.
Exemple 9
Convertir 88,4 m/min en mètres/seconde.
Solution
Nous voulons changer l’unité dans le dénominateur de minutes en secondes. Comme il y a 60 secondes dans 1 minute (60 s = 1 min), nous construisons un facteur de conversion pour que l’unité que nous voulons supprimer, les minutes, soit au numérateur : 1 min/60 s. Appliquez et effectuez le calcul :
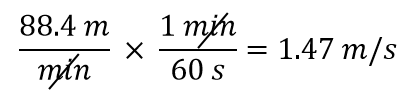
Notez comment le 88,4 va automatiquement dans le numérateur. C’est parce que tout nombre peut être considéré comme étant au numérateur d’une fraction divisée par 1.
Testez vous-même
Convertissez 0,203 m/min en mètres/seconde.
Réponse
0.00338 m/s ou 3,38 × 10-3 m/s
Figure 2.8 How Fast Is Fast?

Source : « Grapevine snail « par Jürgen Schonerisous licence Creative Commons Attribution-Share Alike 3.0 Unported.
.