Ce sont des processus d’apprentissage stochastiques ayant une structure récurrente et sont la base des premières techniques d’optimisation utilisées dans les ANN. La machine de Boltzmann a été inventée par Geoffrey Hinton et Terry Sejnowski en 1985. Plus de clarté peut être observée dans les mots de Hinton sur la machine de Boltzmann.
« Une caractéristique surprenante de ce réseau est qu’il n’utilise que les informations disponibles localement. Le changement de poids ne dépend que du comportement des deux unités qu’il relie, même si le changement optimise une mesure globale » – Ackley, Hinton 1985.
Quelques points importants sur la machine de Boltzmann –
-
Elles utilisent une structure récurrente.
-
Elles sont constituées de neurones stochastiques, qui ont un des deux états possibles, soit 1 ou 0.
-
Certains de ces neurones sont adaptatifs (état libre) et d’autres sont clampés (état figé).
-
Si l’on applique un recuit simulé sur le réseau Hopfield discret, alors il deviendra une machine de Boltzmann.
Objectif de la machine de Boltzmann
L’objectif principal de la machine de Boltzmann est d’optimiser la solution d’un problème. C’est le travail de la machine de Boltzmann d’optimiser les poids et la quantité liés à ce problème particulier.
Architecture
Le schéma suivant montre l’architecture de la machine de Boltzmann. Il est clair, d’après le diagramme, qu’il s’agit d’un tableau bidimensionnel d’unités. Ici, les poids des interconnexions entre les unités sont -p où p > 0. Les poids des auto-connexions sont donnés par b où b > 0.
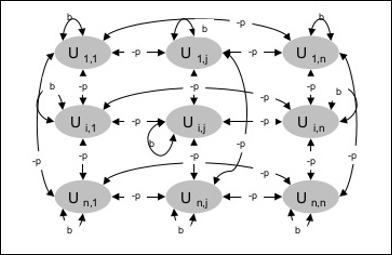
Algorithme d’entraînement
Comme nous savons que les machines de Boltzmann ont des poids fixes, donc il n’y aura pas d’algorithme d’entraînement car nous n’avons pas besoin de mettre à jour les poids du réseau. Cependant, pour tester le réseau, nous devons fixer les poids ainsi que trouver la fonction de consensus (CF).
La machine de Boltzmann possède un ensemble d’unités Ui et Uj et possède des connexions bidirectionnelles sur celles-ci.
-
Nous considérons le poids fixe dire wij.
-
wij ≠ 0 si Ui et Uj sont connectés.
-
Il existe aussi une symétrie dans l’interconnexion pondérée, c’est-à-dire.c’est-à-dire wij = wji.
-
Il existe aussi wii, c’est-à-dire qu’il y aurait l’auto-connexion entre les unités.
-
Pour toute unité Ui, son état ui serait soit 1 soit 0.
L’objectif principal de la machine de Boltzmann est de maximiser la fonction de consensus (FC) qui peut être donnée par la relation suivante
$CF\:=\:\displaystyle\sum\limits_{i}. \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$
Maintenant, lorsque l’état change de 1 à 0 ou de 0 à 1, alors le changement de consensus peut être donné par la relation suivante –
$Delta CF\\ :=\ :(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Here ui est l’état actuel de Ui.
La variation du coefficient (1 – 2ui) est donnée par la relation suivante –
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:is\:currently\ :off\\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
Généralement, l’unité Ui ne change pas d’état, mais si c’est le cas alors l’information résiderait localement à l’unité. Avec ce changement, il y aurait également une augmentation du consensus du réseau.
La probabilité que le réseau accepte le changement d’état de l’unité est donnée par la relation suivante –
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$
Ici, T est le paramètre de contrôle. Il diminuera lorsque CF atteindra la valeur maximale.
Algorithme de test
Etape 1 – Initialiser les éléments suivants pour commencer l’entraînement –
- Poids représentant la contrainte du problème
- Paramètre de contrôle T
Etape 2 – Continuer les étapes 3 à 8, lorsque la condition d’arrêt n’est pas vraie.
Etape 3 – Effectuer les étapes 4 à 7.
Etape 4 – Supposer qu’un des états a changé le poids et choisir les entiers I, J comme valeurs aléatoires entre 1 et n.
Etape 5 – Calculer le changement de consensus comme suit –
$$Delta CF\:=\ :(1\:-\:2u_{i})(w_{ij}\:+\ :\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Etape 6 – Calculer la probabilité que ce réseau accepte le changement d’état
$AF(i,T)\ :=\:\frac{1}{1\:+\:exp}$
Etape 7 – Accepter ou rejeter ce changement comme suit –
Cas I – si R < AF, accepter le changement.
Cas II – si R ≥ AF, rejeter le changement.
Ici, R est le nombre aléatoire entre 0 et 1.
Etape 8 – Réduire le paramètre de contrôle (température) comme suit –
T(nouveau) = 0.95T(old)
Étape 9 – Tester les conditions d’arrêt qui peuvent être les suivantes –
- La température atteint une valeur spécifiée
- Il n’y a pas de changement d’état pour un nombre spécifié d’itérations
.