Barikcentrikus koordináták

Szerző:
Geometria > Koordinátageometria >
Geometria > Síkgeometria > Háromszögek > Háromszögtulajdonságok >

A barikcentrikus koordináták számhármasok (t_1,t_2,t_3), amelyek a DeltaA_1A_2A_2A_3 referenciaháromszög csúcsain elhelyezett tömegeknek felelnek meg. Ezek a tömegek ezután meghatároznak egy P pontot, amely a három tömeg geometriai középpontja, és amelyet a (t_1,t_2,t_3) koordinátákkal azonosítunk. A háromszög csúcsait (1,0,0,0), (0,1,0) és (0,0,1) adja. A barycentrikus koordinátákat Möbius fedezte fel 1827-ben (Coxeter 1969, 217. o.; Fauvel et al. 1993).

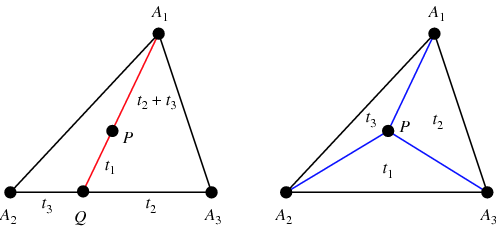
Barycentric

Egy tetszőleges P pont bicentrikus koordinátáinak megtalálásához a t_2 és t_3 pontból Q a A_1P egyenes és a A_2A_3 oldal metszéspontjában található koordinátákat kell megadni, majd határozzuk meg t_1 mint a A_1 pontban lévő t_2+t_3 tömeget, amely a Q pontban lévő P tömeget egyensúlyozza ki, így P lesz a középpont (bal oldali ábra). Továbbá a DeltaA_1A_2P, DeltaA_1A_3P és DeltaA_2A_3P háromszögek területe arányos a P t_3, t_2 és t_1 barycentrikus koordinátáival (jobb oldali ábra; Coxeter 1969, p. 217).

A baricentrikus koordináták homogének, tehát

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

for mu!=0.

Azokat a barycentrikus koordinátákat, amelyeket úgy normalizálunk, hogy a részszögek tényleges területeivé váljanak, homogén barycentrikus koordinátáknak nevezzük. Az olyan módon normalizált barycentrikus koordinátákat, hogy

t_1+t_2+t_3=1,
(2)

hogy a koordináták az eredeti háromszög területével normalizált részháromszögek területét adják, areális koordinátáknak nevezzük (Coxeter 1969, 218. o.). A barycentrikus és az areális koordináták különösen elegáns bizonyításai lehetnek olyan geometriai tételeknek, mint a Routh-tétel, a Ceva-tétel és a Menelaosz-tétel (Coxeter 1969, 219-221. o.).

(Nem feltétlenül homogén) barycentrikus koordináták számos gyakori középpontra a következő táblázatban vannak összefoglalva. A táblázatban a, b és c a háromszög oldalhosszai, s pedig a félperimétere.

háromszög középpontja barycentrikus koordináták
környékpont O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
excenter J_B (a,-b,c)
excenter J_C (a,b,-c)
Gergonne pont Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incentor I (a,b,c)
Nagel pont Na (s-a,s-b,s-c)
ortocentrum H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
szimmetriapont K (a^2,b^2,c^2)
háromszög középpontja G (1,1,1)

Barycentrikus koordinátákban egy egyenesnek lineáris homogén egyenlete van. Különösen a (r_1,r_2,r_3) és (s_1,s_2,s_3) pontokat összekötő egyenesnek

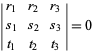|r_1 r_2 r_3 egyenlete van; s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 és 57; Coxeter 1969, 219. o.; Bottema 1982). Ha egy DeltaP_1P_2P_3 háromszög P_i csúcsai (x_i,y_i,z_i) barycentrikus koordinátákkal rendelkeznek, akkor a háromszög területe

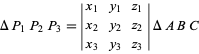DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Szólj hozzá!