Az ANN-ben használt korai optimalizálási technikák alapját képező sztochasztikus tanulási folyamatok rekurrens szerkezetűek. A Boltzmann-gépet Geoffrey Hinton és Terry Sejnowski találta fel 1985-ben. A Boltzmann-gépről Hinton szavaiból még világosabban kiolvasható:
“Ennek a hálózatnak meglepő tulajdonsága, hogy csak a helyileg rendelkezésre álló információt használja fel. A súlyváltozás csak az általa összekötött két egység viselkedésétől függ, még akkor is, ha a változás egy globális mértéket optimalizál.” – Ackley, Hinton 1985.
Néhány fontos pont a Boltzmann-gépről –
-
Rekurrens szerkezetet használnak.
-
Sztochasztikus neuronokból állnak, amelyeknek két lehetséges állapot közül az egyik, 1 vagy 0 lehet.
-
A neuronok egy része adaptív (szabad állapotú), más része pedig kapcsolt (befagyasztott állapotú).
-
Ha a diszkrét Hopfield-hálózatra szimulált lágyítást alkalmazunk, akkor Boltzmann-gép lesz belőle.
A Boltzmann-gép célja
A Boltzmann-gép fő célja egy probléma megoldásának optimalizálása. A Boltzmann-gép feladata az adott problémához kapcsolódó súlyok és mennyiségek optimalizálása.
Építészet
A következő ábra a Boltzmann-gép felépítését mutatja. Az ábrán jól látható, hogy egy kétdimenziós egységtömbről van szó. Itt az egységek közötti összeköttetések súlyai -p, ahol p > 0. Az önkapcsolatok súlyait b adja, ahol b > 0.
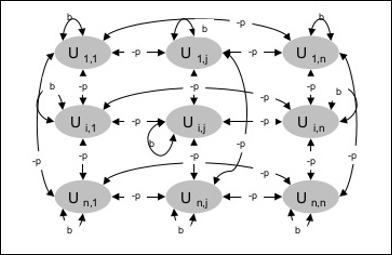
Tréningalgoritmus
Mivel tudjuk, hogy a Boltzmann-gépek súlyai rögzítettek, ezért nem lesz tréningalgoritmus, mivel nem kell frissítenünk a hálózat súlyait. A hálózat teszteléséhez azonban be kell állítanunk a súlyokat, valamint meg kell találnunk a konszenzusfüggvényt (CF).
A Boltzmann-gép Ui és Uj egységekből áll, és ezeken kétirányú kapcsolatok vannak.
-
Megfigyeljük a fix súlyt, mondjuk wij.
-
wij ≠ 0, ha Ui és Uj összekapcsolódik.
-
A súlyozott összekapcsolódásban is létezik egy szimmetria, i.azaz wij = wji.
-
wii is létezik, azaz az egységek között fennállna az önkapcsolás.
-
Minden Ui egység esetében az ui állapota vagy 1 vagy 0 lenne.
A Boltzmann-gép fő célja a konszenzusfüggvény (CF) maximalizálása, amely a következő összefüggéssel adható meg
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
Most, amikor az állapot 1-ről 0-ra vagy 0-ról 1-re változik, akkor a konszenzus változása a következő összefüggéssel adható meg –
$$\\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Itt ui az Ui aktuális állapota.
A (1 – 2ui) együtthatóváltozást a következő összefüggés adja –
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:is\:currently\:off\\\-1, & U_{i}\:is\:jelenleg\:on\end{esetek}$$
Az Ui egység általában nem változtatja meg az állapotát, de ha mégis, akkor az információ lokálisan az egységnél maradna. Ezzel a változással a hálózat konszenzusa is növekedne.
A hálózat valószínűségét, hogy elfogadja az egység állapotváltozását, a következő összefüggés adja –
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Itt T a vezérlő paraméter. Ez csökken, ahogy a CF eléri a maximális értéket.
Tesztalgoritmus
1. lépés – A képzés megkezdéséhez inicializáljuk a következőket –
- A probléma kényszerét reprezentáló súlyok
- Vezérlő paraméter T
2. lépés – A 3-8. lépés folytatása, ha a megállási feltétel nem igaz.
3. lépés – Végezzük el a 4-7. lépést.
4. lépés – Tegyük fel, hogy az egyik állapot súlya megváltozott, és válasszuk ki az I, J egész számokat 1 és n közötti véletlen értékként.
5. lépés – Számítsuk ki a konszenzus változását az alábbiak szerint –
$$$\\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$$
6. lépés – Számítsuk ki annak valószínűségét, hogy ez a hálózat elfogadja az állapotváltozást
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
7. lépés – Fogadjuk el vagy utasítsuk el ezt a változást az alábbiak szerint –
I. eset – ha R < AF, fogadjuk el a változást.
II. eset – ha R ≥ AF, utasítsuk el a módosítást.
Itt R a 0 és 1 közötti véletlen szám.
8. lépés – A szabályozási paraméter (hőmérséklet) csökkentése az alábbiak szerint –
T(új) = 0.95T(régi)
9. lépés – A megállási feltételek vizsgálata, amelyek a következők lehetnek –
- A hőmérséklet elér egy meghatározott értéket
- Nincs állapotváltozás egy meghatározott számú iteráción keresztül
.