Introduction
Az enzimek aktív helyei általában aminosavmaradványokból állnak; attól függően, hogy mely aminosavmaradványok vannak jelen, a szubsztrát specifitása nagyban változhat. A pH-szinttől függően az enzim fizikai tulajdonságai (főként elektromos töltése) megváltozhatnak. Az elektromos töltés változása megváltoztathatja az aktív hely aminosavmaradványai és a beérkező szubsztrát közötti kölcsönhatást. Ezzel együtt a szubsztrát hidrogénkötés vagy van der Waals-erők révén kötődhet az aktív helyhez. Amint a szubsztrát az aktív helyhez kötődik, enzim-szubsztrát komplexet képez, amely aztán további kémiai reakciókban vesz részt.
Hogy egy enzim aktív legyen, és energetikailag kedvező legyen ahhoz, hogy egy kémiai reakció előrehaladhasson, a szubsztrátnak az enzim “aktív helyéhez” kell kötődnie. Az aktív helyet úgy lehet elképzelni, mint egy zárat és a szubsztrátot, mint egy kulcsot; ez az úgynevezett zár és kulcs modell. A kulcsot (szubsztrát) be kell helyezni és el kell forgatni (kémiai reakció), majd a zár (enzim) kinyílik (termékek keletkezése). Megjegyzendő, hogy egy enzimnek egynél több aktív helye is lehet. Az aktív hely-szubsztrát kapcsolatra vonatkozó másik elmélet az indukált illeszkedés elmélete, amely teljesen ellentétes a zár és kulcs elmélettel (ahol az aktív hely látszólag rugalmatlan). Az indukált illeszkedés elméletében az enzim aktív helye nagyon rugalmas, és csak akkor változtatja meg a konformációját, amikor a szubsztrát kötődik hozzá.
Az enzimek katalizátorként úgy működnek, hogy csökkentik az enzim-szubsztrát komplex aktiválásának Gibbs-féle szabad energiáját. Az alábbi két ábra egy enzimes alapreakciót mutat be katalizátorral és katalizátor nélkül:
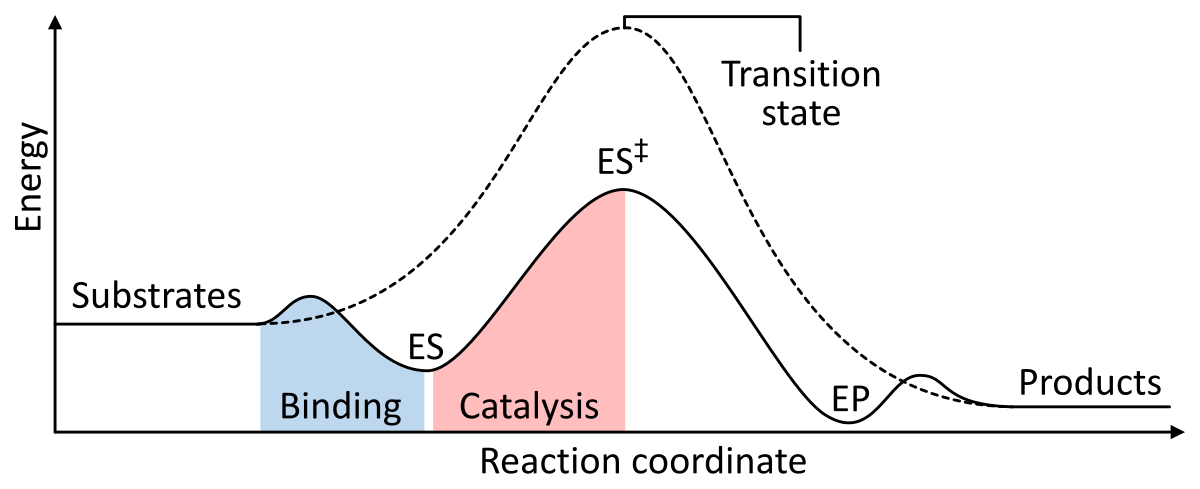
1. ábra: Egy kémiai reakció szakaszainak energiái. Katalizálatlanul (szaggatott vonal) a szubsztrátoknak sok aktiválási energiára van szükségük ahhoz, hogy elérjenek egy átmeneti állapotot, amely aztán alacsonyabb energiájú termékekké bomlik. Ha enzimkatalizált (folytonos vonal), az enzim megköti a szubsztrátokat (ES), majd stabilizálja az átmeneti állapotot (ES‡), hogy csökkentse a termékek (EP) keletkezéséhez szükséges aktiválási energiát, amelyek végül felszabadulnak. a Wikipédiából.
Az enzim hatékonysága a következőképpen határozható meg: tekintsünk egy egyszerű enzimatikus reakciót:
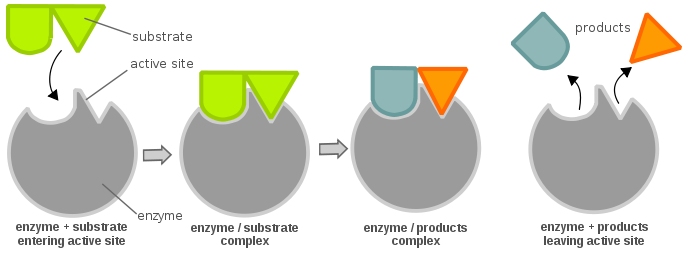
A német biokémikus Leonor Michaelis és a kanadai biokémikus Maud Menten levezette az ezt a rendszert leíró, később “Michaelis-Menten-egyenletként” ismert egyenletet, amely az alábbiakban látható:
\}{K_M + } \tag{1}\]
Ez az egyenlet megadja a reakció sebességét egy adott szubsztrátkoncentráció mellett, feltételezve egy ismert Vmax-ot, ami a reakció maximális sebessége, és KM-et, a Michaelis-állandót. A Michaelis-Menten gyakorlati alkalmazásakor azonban gyakran a V0-t mérik, és a Vmax-ot telítésként vagy platóként figyelik meg az adatdiagramon. Mivel a szubsztrátkoncentráció ismert, általában a KM az érdekes számított érték.
Az \(K_M\) esetében tegyük fel, hogy \(V_0= \dfrac{V_{max}}{2}\):
\}{K_M + } \tag{2}\]
\) \dfrac{V_{max}}{2} = V_{max} \tag{3}\]
\ = \dfrac{V_{max}}{\dfrac{V_{max}}{2}} \tag{4} \\]
\ = 2 \tag{5}\]
\ \tag{6}\]
A Michaelis-állandó úgy képzelhető el, mint az a sebesség, amellyel a szubsztrát az enzimről leválik, ami vagy a szubsztrát-enzim komplex termékké válásának, vagy a szubsztrátnak az enzimhez való leválásának eseményeiben következhet be. A KM egyenletként ábrázolható.
\
Ahol k-1 az a sebességi állandó, amelynél a szubsztrát az enzimhez nem kötődik, ami az enzim-szubsztrát komplex disszociációját eredményezi, k2 az a sebességi állandó, ahol a szubsztrát-enzim komplex eltűnik és termékké alakul, és K1 a szubsztrát-enzim komplex képződésének sebességi állandója. A KM tehát úgy tekinthető, mint a szubsztrát-enzim komplex eltűnésének sebessége osztva a szubsztrát-enzim komplex képződésének sebességével, ami azt a szintet jelenti, amikor a szubsztrát fele az enzimhez kötődik. A KM hasznos indikátora az inhibitor jelenlétének, mert megnézhetjük a KM változását, és összehasonlíthatjuk a kontrollunkkal (biológiai rendszerek, amelyekről tudjuk, hogy nulla inhibitor jelenléte van). A KM egy függő változó, és értéke számos ok miatt változhat, beleértve a rendszer pH-szintjét, a hőmérsékletet vagy bármely más olyan körülményt, amely befolyásolhatja a kémiai reakciót. A kis KM azt jelzi, hogy a szubsztrátnak nagy az affinitása az enzimhez.
A Michaelis-Menten-egyenlet akkor a leghasznosabb az enzim hatékonyságának mérésére, ha a v0-t a , ellenében ábrázoljuk az alábbiak szerint:
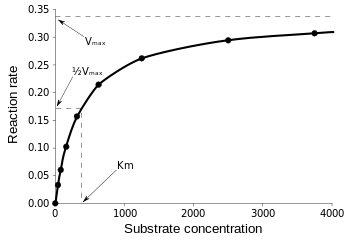
3. ábra: A reakciósebesség és a Michaelis-Menten-állandó diagramja. a Wikipédiából.
Vmax az a maximális sebesség, amellyel a reakció lefuthat, függetlenül a , ami azt jelenti, hogy még ha több szubsztrátot adunk is hozzá, a reakció nem mehet gyorsabban. Ez azért van így, mert a Vmax értéknél az enzim összes aktív helye foglalt. Az enzimkinetikai egyenletek különböző formáira vonatkozó magyarázatok után eljutottunk a katalitikus hatékonyságra vonatkozó következtetésünkhöz. Visszautalva a 3. ábrára, az alábbiakat kapjuk:
\_o}{\dfrac{k_{-1} + k_2}{k_1} + }\right) \tag{8}\]
Megjegyezzük, hogy \(k_2\) egy irreverzibilis reakciót ír le, szemben az egyensúlyi kifejezéssel, ha összehasonlítjuk a k-1 és k1 értékekkel. k2 itt kcat néven is ismert, az enzim katalitikus hatékonysága. Az előző tárgyalásból v0 a mért reakciósebesség, ami a termékképződést jelenti az idő múlásával, így arra következtethetünk, hogy az egyenlet a következőképpen nézne ki:
\}{dt} = k_2_0 \tag{9}\]
Ahol 0 az enzim teljes koncentrációja.
Azt is tudjuk, hogy VMax akkor figyelhető meg, amikor az összes enzim-szubsztrát komplex eltűnik és termékké alakul, így a következő feltételezést tehetjük:
\_0 \tag{10} \]
és átrendezés után ezt az egyenletet kapjuk:
\_0} \tag{11}\]
Ez a katalitikus hatékonyság kiszámítására szolgáló egyenlet, amelyet a kísérletekből származó adatok megszerzése és a Michaelis-Menten-egyenlet használata után kell használnunk. Nagyobb kcat esetén az enzim hatékony, mert kevesebb enzimre van szükség
.