A konfúziós mátrix egy olyan táblázat, amelyet gyakran használnak egy osztályozási modell (vagy “osztályozó”) teljesítményének leírására egy olyan tesztadathalmazon, amelynek valódi értékei ismertek. Maga a zavarmátrix viszonylag egyszerűen érthető, de a kapcsolódó terminológia zavaró lehet.
A zavarmátrix terminológiájához szerettem volna egy “gyors útmutatót” készíteni, mert nem találtam olyan meglévő forrást, amely megfelelt volna a követelményeimnek: kompakt megjelenítés, tetszőleges változók helyett számok használata, és mind képletekben, mind mondatokban történő magyarázat.
Kezdjük egy bináris osztályozóra vonatkozó példakonfúziós mátrixszal (bár könnyen kiterjeszthető kettőnél több osztály esetére is):
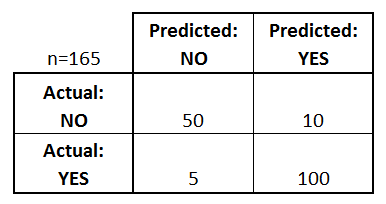
Mit tudhatunk meg ebből a mátrixból?
- Két lehetséges megjósolt osztály van: “igen” és “nem”. Ha például egy betegség jelenlétét jósolnánk meg, akkor az “igen” azt jelentené, hogy megvan a betegség, a “nem” pedig azt, hogy nincs meg a betegség.
- Az osztályozó összesen 165 jóslatot tett (pl., 165 beteget vizsgáltak az adott betegség jelenlétére).
- A 165 esetből az osztályozó 110 alkalommal “igen”-t, 55 alkalommal pedig “nem”-et jósolt.
- A valóságban a mintában 105 betegnek van a betegség, 60 betegnek pedig nincs.
Meghatározzuk most a legalapvetőbb kifejezéseket, amelyek egész számok (nem arányok):
- igaz pozitívak (true positive, TP):
- igaz negatívok (TN): Nemet jósoltunk, és nincs meg a betegségük.
- hamis pozitív esetek (FP): Igent jósoltunk, de valójában nincs meg a betegségük. (Más néven “I. típusú hiba”.)
- hamis negatív (FN): Nemet jósoltunk, de valójában megvan a betegség. (Más néven “II. típusú hiba”.)
Ezeket a kifejezéseket hozzáadtam a zavarmátrixhoz, és hozzáadtam a sor- és oszlopösszegeket is:
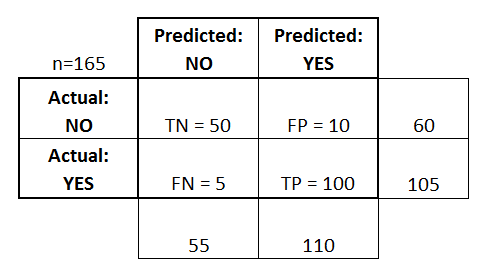
Ez egy lista a bináris osztályozó zavarmátrixából gyakran kiszámított arányokról:
- Pontosság:
- (TP+TN)/összesen = (100+50)/165 = 0,91
- Téves osztályozási arány: Összességében milyen gyakran hibázik?
- (FP+FN)/összesen = (10+5)/165 = 0,09
- egyenértékű 1 mínusz pontosság
- más néven “hibaarány”
- Igaz pozitív arány:
- TP/tényleges igen = 100/105 = 0,95
- mint “érzékenység” vagy “visszahívás”
- Hamis pozitív arány:
- FP/tényleges nem = 10/60 = 0,17
- True Negative Rate:
- TN/tényleges nem = 50/60 = 0,83
- egyenértékű 1 mínusz hamis pozitív arány
- más néven “specificitás”
- precizitás:
- TP/előrejelzett igen = 100/110 = 0,91
- Prevalencia: Milyen gyakran fordul elő ténylegesen az igen állapot a mintánkban?
- tényleges igen/összességében = 105/165 = 0,64
Egy pár másik kifejezést is érdemes megemlíteni:
- Null Error Rate: Ez az, hogy milyen gyakran tévednél, ha mindig a többségi osztályt jósolnád meg. (Példánkban a null hibaarány 60/165=0,36 lenne, mert ha mindig igent jósolnál, akkor csak a 60 “nem” esetben tévednél). Ez egy hasznos alapszintű mérőszám lehet, amellyel összehasonlíthatja az osztályozóját. Azonban egy adott alkalmazáshoz a legjobb osztályozó néha magasabb hibaaránnyal fog rendelkezni, mint a nullhibaarány, amint azt a pontossági paradoxon is mutatja.
- Cohen Kappa: Ez lényegében annak a mérőszáma, hogy az osztályozó mennyire jól teljesített ahhoz képest, hogy milyen jól teljesített volna pusztán a véletlen alapján. Más szóval, egy modellnek magas Kappa pontszáma lesz, ha nagy a különbség a pontosság és a nullhibaarány között. (További részletek a Cohen Kappáról.)
- F-pontszám: Ez a valódi pozitív arány (recall) és a pontosság súlyozott átlaga. (További részletek az F-pontszámról.)
- ROC-görbe: Ez egy általánosan használt grafikon, amely összefoglalja egy osztályozó teljesítményét az összes lehetséges küszöbértékre vonatkozóan. Úgy jön létre, hogy a True Positive Rate (y-tengely) és a False Positive Rate (x-tengely) arányát ábrázoljuk, ahogy a megfigyelések adott osztályba sorolásának küszöbértékét változtatjuk. (További részletek a ROC-görbékről.)
Végezetül pedig azoknak, akik a Bayes-statisztika világából érkeztek, íme egy gyors összefoglaló ezekről a kifejezésekről az Alkalmazott prediktív modellezésből:
A Bayes-statisztikával kapcsolatban az érzékenység és a specificitás a feltételes valószínűségek, a prevalencia az előzetes, a pozitív/negatív előrejelzett értékek pedig az utólagos valószínűségek.
Még többet szeretne megtudni?
Az új, 35 perces, Making sense of the confusion matrix című videómban mélyebben elmagyarázom ezeket a fogalmakat, és több haladó témával is foglalkozom:
- Hogyan számítsuk ki a pontosságot és a visszahívást többosztályos problémák esetén
- Hogyan elemezzünk egy 10 osztályos zavarmátrixot
- Hogyan válasszuk ki a megfelelő értékelési metrikát a problémánkhoz
- Miért a pontosság gyakran félrevezető metrika
Mondja el, ha bármilyen kérdése van!