Lineráris egyenletrendszer
A lineáris egyenletek aluldeterminált rendszere több ismeretlent tartalmaz, mint egyenletet, és általában végtelen számú megoldással rendelkezik. Az alábbi ábra egy ilyen egyenletrendszert y = D x {\displaystyle \mathbf {y} =D\mathbf {x} }

ahol x-re szeretnénk megoldást találni {\displaystyle \mathbf {x} }

.
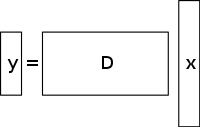
Egy ilyen rendszer megoldásának kiválasztásához szükség szerint további megkötéseket vagy feltételeket (például simaságot) kell szabnunk. A tömörített érzékelésben a ritkasági megkötést adjuk hozzá, amely csak olyan megoldásokat enged meg, amelyek kis számú nem nulla együtthatóval rendelkeznek. Nem minden aluldeterminált lineáris egyenletrendszer rendelkezik ritka megoldással. Ha azonban az aluldeterminált rendszernek van egyedi ritka megoldása, akkor a tömörített érzékelési keretrendszer lehetővé teszi ennek a megoldásnak a visszanyerését.
Megoldási / rekonstrukciós módszer

A tömörített érzékelés kihasználja a sok érdekes jel redundanciáját – ezek nem tiszta zajok. Különösen sok jel ritka, azaz sok olyan együtthatót tartalmaz, amely valamely tartományban ábrázolva közel vagy egyenlő nullával. Ez ugyanaz a felismerés, amelyet a veszteséges tömörítés számos formája használ.
A tömörített érzékelés általában úgy kezdődik, hogy a minták súlyozott lineáris kombinációját, amelyet tömörítő méréseknek is neveznek, olyan alapon végezzük, amely eltér attól az alaptól, amelyben a jelről ismert, hogy ritka. Az Emmanuel Candès, Justin Romberg, Terence Tao és David Donoho által talált eredmények azt mutatták, hogy ezeknek a tömörítő méréseknek a száma kicsi lehet, és mégis tartalmazhatja szinte az összes hasznos információt. Ezért a kép visszaalakítása a tervezett tartományba egy aluldeterminált mátrixegyenlet megoldását jelenti, mivel a felvett tömörítő mérések száma kisebb, mint a teljes kép pixeleinek száma. Ha azonban hozzáadjuk azt a megkötést, hogy a kezdeti jel ritka legyen, akkor megoldható ez az aluldeterminált lineáris egyenletrendszer.
Az ilyen problémák legkisebb négyzetek szerinti megoldása az L 2 {\displaystyle L^{2}}

normát – vagyis a rendszerben lévő energia mennyiségének minimalizálását. Ez matematikailag általában egyszerű (csak egy mátrixszorzást igényel a mintavételezett bázis pszeudoinverzével). Ez azonban számos olyan gyakorlati alkalmazás esetében, ahol az ismeretlen együtthatók nem nulla energiával rendelkeznek, rossz eredményekhez vezet.
A ritkasági megkötés érvényesítésére az aluldeterminált lineáris egyenletrendszer megoldása során minimalizálhatjuk a megoldás nem nulla összetevőinek számát. A vektor nem nulla összetevőinek számát számláló függvényt L 0 {\displaystyle L^{0}}

“normának” nevezte David Donoho.
Candès és társai bebizonyították, hogy sok probléma esetén valószínű, hogy az L 1 {\displaystyle L^{1}}

norma egyenértékű az L 0 {\displaystyle L^{0}}

normával, technikai értelemben: Ez az ekvivalenciaeredmény lehetővé teszi az L 1 {\displaystyle L^{1}}

problémát, ami egyszerűbb, mint az L 0 {\displaystyle L^{0}}

problem. A legkisebb L 1 {\displaystyle L^{1}}

normát viszonylag könnyen kifejezhető lineáris programként, amelyre már léteznek hatékony megoldási módszerek. Ha a mérések véges mennyiségű zajt tartalmazhatnak, akkor a lineáris programozással szemben előnyben részesítjük a báziskövetéses zajmentesítést, mivel ez megőrzi a ritkaságot a zajjal szemben, és gyorsabban megoldható, mint egy egzakt lineáris program.
Teljes variáción alapuló CS-rekonstrukció
Motiváció és alkalmazások
A TV regularizáció szerepe
A totálvariáció tekinthető egy nemnegatív valós értékű függvénynek, amelyet a valós értékű függvények terében (egyváltozós függvények esetén) vagy az integrálható függvények terében (többváltozós függvények esetén) definiálunk. Különösen jelek esetén a teljes variáció a jel abszolút gradiensének integráljára utal. A jel- és képrekonstrukcióban totálvariációs regularizációként alkalmazzák, ahol az alapelv az, hogy a túlzott részleteket tartalmazó jelek nagy totálvariációval rendelkeznek, és hogy ezen részletek eltávolítása – a fontos információk, például az élek megtartása mellett – csökkenti a jel totálvariációját, és a jel tárgya közelebb kerül a probléma eredeti jeléhez.
A jel- és képrekonstrukció céljából l 1 {\displaystyle l1}

minimalizálási modelleket használnak. Más megközelítések közé tartozik a legkisebb négyzetek is, ahogyan azt már korábban tárgyaltuk ebben a cikkben. Ezek a módszerek rendkívül lassúak, és a jel nem túl tökéletes rekonstrukcióját adják vissza. A jelenlegi CS regularizációs modellek úgy próbálják kezelni ezt a problémát, hogy az eredeti kép ritkasági priorait beépítik, amelyek közül az egyik a teljes variáció (TV). A hagyományos TV-megközelítéseket úgy tervezték, hogy darabonként állandó megoldásokat adjanak. Ezek közül néhány (az előbbiekben tárgyaltak szerint) – korlátozott l1-minimalizálás, amely iteratív sémát használ. Ez a módszer, bár gyors, később az élek túlsimításához vezet, ami elmosódott képszéleket eredményez. A képeken a nagy gradiensérték-magnitúdók hatásának csökkentésére iteratív újrasúlyozással ellátott TV-módszereket alkalmaztak. Ezt a komputertomográfiás (CT) rekonstrukcióban használták az élmegőrző teljes variáció néven ismert módszerként. Mivel azonban a gradiensnagyságokat az adathűség és a regularizációs kifejezések közötti relatív büntetősúlyok becslésére használják, ez a módszer nem robusztus a zajjal és a műalkotásokkal szemben, és nem elég pontos a CS-kép/jel rekonstrukciójához, ezért nem képes megőrizni a kisebb struktúrákat.
A legújabb előrelépés ebben a problémában egy iteratív irányított TV finomítás használata a CS rekonstrukcióhoz. Ez a módszer 2 szakaszból állna: az első szakasz megbecsülné és finomítaná a kezdeti orientációs mezőt – amelyet az adott kép zajos, pontonkénti kezdeti becslésként definiálnak, az élek felismerésén keresztül. A második szakaszban a CS rekonstrukciós modell az irányított TV-szabályozó felhasználásával kerül bemutatásra. Ezekről a TV-alapú megközelítésekről – az iteratívan újrasúlyozott l1 minimalizálásról, az élmegőrző TV-ről és az irányított orientációs mezőt és TV-t használó iteratív modellről – az alábbiakban találhatók további részletek.
Létező megközelítések
Iteratívan újrasúlyozott l 1 {\displaystyle l_{1}}


minimalizálás

A CS rekonstrukciós modellekben a korlátozott l 1 {\displaystyle l_{1}}}

minimalizálása során a nagyobb együtthatókat erősen büntetik az l 1 {\displaystyle l_{1}}

norm. Javasolták az l 1 {\displaystyle l_{1}} súlyozott megfogalmazását.

minimalizálását, amelynek célja a nem nulla együtthatók demokratikusabb büntetése. A megfelelő súlyok megkonstruálására iteratív algoritmust alkalmazunk. Minden egyes iteráció során egy l 1 {\displaystyle l_{1}}

minimalizálási feladatot egy olyan konkáv büntetőfüggvény lokális minimumának megtalálásával, amely jobban hasonlít az l 0 {\displaystyle l_{0}}

norm. Egy további paramétert, általában a büntetőfüggvény görbéjének éles átmeneteit elkerülendő, az iterációs egyenletbe bevezetünk a stabilitás biztosítása érdekében, és azért, hogy az egyik iterációban adott nulla becslés ne feltétlenül vezessen nulla becsléshez a következő iterációban. A módszer lényegében az aktuális megoldás felhasználásával számítja ki a következő iterációban használandó súlyokat.
Hátrányok és előnyök
A korai iterációkban pontatlan mintabecsléseket találhatunk, azonban ez a módszer egy későbbi szakaszban ezeket lemintavételezi, hogy nagyobb súlyt adjon a kisebb, nem nulla jelbecsléseknek. Az egyik hátránya, hogy szükség van egy érvényes kezdőpont meghatározására, mivel a függvény konkávsága miatt nem biztos, hogy minden alkalommal globális minimumot kapunk. Egy másik hátrány, hogy ez a módszer hajlamos a kép gradiensét egységesen büntetni, függetlenül az alapul szolgáló képi struktúráktól. Ez az élek túlzott simítását okozza, különösen az alacsony kontrasztú régiókban, ami az alacsony kontrasztú információk elvesztéséhez vezet. E módszer előnyei közé tartozik: a mintavételi sebesség csökkentése ritka jelek esetén; a kép rekonstrukciója, miközben robusztus a zaj és más artefaktumok eltávolításával szemben; és nagyon kevés iteráció használata. Ez segíthet a ritka gradiensű képek helyreállításában is.
Az alábbi ábrán látható P1 az iteratív rekonstrukciós folyamat első lépésére, a legyezősugár geometria P vetületi mátrixára utal, amelyet az adathűség kifejezés korlátoz. Ez tartalmazhat zajt és artefaktumokat, mivel nem történik regularizáció. A P1 minimalizálását a konjugált gradiens legkisebb négyzetek módszerével oldjuk meg. A P2 az iteratív rekonstrukciós folyamat második lépésére utal, amelyben az élmegőrző teljes variációs regularizációs kifejezést használja a zaj és a műtárgyak eltávolítására, és ezáltal a rekonstruált kép/jel minőségének javítására. A P2 minimalizálása egyszerű gradiens süllyedéses módszerrel történik. A konvergenciát úgy határozzuk meg, hogy minden egyes iteráció után megvizsgáljuk a kép pozitivitását, ellenőrizve, hogy f k – 1 = 0 {\displaystyle f^{k-1}=0}

arra az esetre, ha f k – 1 < 0 {\displaystyle f^{k-1}<0}

(Megjegyzendő, hogy f {\displaystyle f}

a betegkép különböző voxeleinél mért különböző lineáris röntgensugárzási együtthatókra utal).
Széleket megőrző teljes variáció (TV) alapú tömörített érzékelés

Ez egy iteratív CT-rekonstrukciós algoritmus széleket megőrző TV regularizációval a CT-képek rekonstruálására alacsony dózisú CT-n kapott, erősen alulmintavételezett adatokból alacsony áramszintek (milliamper) révén. A képalkotó dózis csökkentése érdekében az egyik alkalmazott megközelítés a szkenner detektorai által felvett röntgensugaras vetületek számának csökkentése. A CT-kép rekonstruálásához használt elégtelen vetületi adatok azonban csíkos műtermékeket okozhatnak. Továbbá, ha ezeket az elégtelen vetületeket a szabványos TV-algoritmusokban használják, a probléma aluldeterminálttá válik, és így végtelen sok lehetséges megoldáshoz vezet. Ebben a módszerben az eredeti TV-normához egy további büntető súlyozott függvényt rendelünk. Ez lehetővé teszi az éles intenzitásbeli megszakítások könnyebb felismerését a képeken, és ezáltal a súly kiigazítását a visszanyert élinformáció tárolására a jel/kép rekonstrukciós folyamat során. A σ paraméter \displaystyle \sigma }

szabályozza a széleken lévő pixelekre alkalmazott simítás mértékét, hogy megkülönböztesse őket a nem széleken lévő pixelektől. A σ {\displaystyle \sigma } értéke

értékét a gradiens nagyságának hisztogramja alapján adaptívan változtatja úgy, hogy a pixelek bizonyos százalékában a gradiens értéke nagyobb legyen, mint σ {\displaystyle \sigma }

. Az élt megőrző teljes variációs kifejezés így ritkábbá válik, és ez felgyorsítja a megvalósítást. Egy kétlépéses iterációs eljárást, az úgynevezett előre-hátra osztó algoritmust használjuk. Az optimalizálási problémát két részproblémára bontjuk, amelyeket a konjugált gradiens legkisebb négyzetek módszerével, illetve az egyszerű gradiens süllyedés módszerével oldunk meg. A módszer akkor áll le, ha a kívánt konvergencia elérte a kívánt konvergenciát, vagy ha az iterációk maximális számát elérte.
Hátrányok és hátrányok
A módszer hátrányai közé tartozik a kisebb struktúrák hiánya a rekonstruált képen és a képfelbontás romlása. Ez az élmegőrző TV-algoritmus azonban kevesebb iterációt igényel, mint a hagyományos TV-algoritmus. A rekonstruált képek vízszintes és függőleges intenzitásprofilját elemezve látható, hogy a perempontokon éles ugrások, a nem perempontokon pedig elhanyagolható, kisebb ingadozás tapasztalható. Így ez a módszer a TV-módszerhez képest alacsony relatív hibához és magasabb korrelációhoz vezet. Emellett hatékonyan elnyomja és eltávolítja a képzaj minden formáját és a képi leleteket, például a csíkozódást.
Iteratív modell irányított orientációs mező és irányított teljes variáció felhasználásával
Az élek és a textúra részleteinek túlzott simításának megakadályozására, valamint a zajjal és leletekkel szemben pontos és robusztus rekonstruált CS-kép előállítására ezt a módszert alkalmazzuk. Először a kép I {\displaystyle I} zajos pontonkénti orientációs mezejének kezdeti becslése

, d ^ {\displaystyle {\hat {d}}}

, kapjuk. Ezt a zajos orientációs mezőt úgy határozzuk meg, hogy egy későbbi fázisban finomítható legyen az orientációs mező becslésére gyakorolt zajhatások csökkentése érdekében. Ezután egy durva orientációs mezőbecslést vezetünk be a struktúra tenzor alapján, amelyet a következőképpen fogalmazunk meg: J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 12 J 22 ) {\displaystyle J_{\rho }(\nabla I_{\sigma })=G_{\rho }*(\nabla I_{\sigma }\szor \nabla I_{\sigma })={\begin{pmatrix}J_{11}&J_{12}\\\J_{12}&J_{22}\end{pmatrix}}}

. Itt J ρ {\displaystyle J_{\rho}}

a kép (i,j) képpontjához tartozó struktúra tenzorra utal, amelynek standard eltérése ρ {\displaystyle \rho }

. G {\displaystyle G}

a Gauss-kernel ( 0 , ρ 2 ) {\displaystyle (0,\rho ^{2})}

standard eltéréssel ρ {\displaystyle \rho }

. σ {\displaystyle \sigma } .

az I {\displaystyle I} kép kézzel meghatározott paraméterére utal.

, amely alatt az élérzékelés érzéketlen a zajra. ∇ I σ {\displaystyle \nabla I_{\sigma }}

a kép gradiensére utal I {\displaystyle I}

és ( ∇ I σ ⊗ ∇ I σ ) {\displaystyle (\nabla I_{\sigma }\otimes \nabla I_{\sigma })}

az e gradiens felhasználásával kapott tenzorproduktumra utal.
A kapott szerkezeti tenzort egy G {\displaystyle G} Gaussi kernellel konvolváljuk.

az orientációs becslés pontosságának javítása érdekében σ {\displaystyle \sigma }

nagy értékekre van beállítva az ismeretlen zajszintek figyelembevétele érdekében. A kép minden egyes (i,j) pixelére a J struktúra-tenzor egy szimmetrikus és pozitív féldefinit mátrix. A kép összes pixelének konvolválása G {\displaystyle G}

, a J {\displaystyle J} ortonormális ω és υ sajátvektorait adja.

mátrixot. ω a legnagyobb kontraszttal rendelkező domináns orientáció irányába mutat, υ pedig a legkisebb kontraszttal rendelkező szerkezeti orientáció irányába. Az orientációs mező durva kezdeti becslése d ^ {\displaystyle {\hat {d}}}

a d ^ {\displaystyle {\hat {d}}}

= υ. Ez a becslés erős élek esetén pontos. Gyenge éleknél vagy zajos régiókban azonban csökken a megbízhatósága.
E hátrány leküzdésére egy finomított orientációs modellt definiálunk, amelyben az adattétel csökkenti a zaj hatását és javítja a pontosságot, míg a második büntetőtétel az L2-normával egy hűségtétel, amely biztosítja a kezdeti durva becslés pontosságát.
Ezt az orientációs mezőt az egyenleten keresztül vezetjük be a CS-rekonstrukció irányított teljes variáció optimalizálási modelljébe: m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}

. X {\displaystyle \mathrm {X} }

az objektív jel, amelyet vissza kell nyerni. Y a megfelelő mérési vektor, d az iteratívan finomított orientációs mező és Φ {\displaystyle \Phi }

a CS mérési mátrix. Ez a módszer néhány iteráción megy keresztül, ami végül konvergenciához vezet. d ^ {\displaystyle {\hat {d}}}

a rekonstruált kép X k – 1 {\displaystyle X^{k-1}} orientációs mezőjének közelítő becslése.

az előző iterációból (a konvergencia és a későbbi optikai teljesítmény ellenőrzéséhez az előző iterációt használjuk). Az X {\displaystyle \mathrm {X} } által reprezentált két vektormezőre vonatkozóan

és d {\displaystyle d}

, X ∙ d {\displaystyle \mathrm {X} \bullet d}

az X {\displaystyle \mathrm {X} } megfelelő vízszintes és függőleges vektorelemeinek szorzatára utal.

és d {\displaystyle d}

, majd ezek utólagos összeadása. Ezeket az egyenleteket konvex minimalizálási problémák sorozatára redukáljuk, amelyeket aztán a változófelosztás és a kiterjesztett Lagrange-féle (FFT-alapú gyors megoldó zárt formájú megoldással) módszerek kombinációjával oldunk meg. Ez (Augmented Lagrangian) egyenértékűnek tekinthető az osztott Bregman-iterációval, amely biztosítja e módszer konvergenciáját. A d orientációs mezőt úgy definiáljuk, hogy egyenlő ( d h , d v ) {\displaystyle (d_{h},d_{v})}

, ahol d h , d v {\displaystyle d_{h}},d_{v}}}

határozzák meg a d {\displaystyle d} vízszintes és függőleges becslését.

.

A kiterjesztett Lagrange-módszer az orientációs mezőre, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}}\ \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}}

, magában foglalja a d h , d v , H , V {\displaystyle d_{h},d_{v},H,V} inicializálását.

, majd az L 1 {\displaystyle L_{1}} közelítő minimalizálójának megtalálása.

ezen változók tekintetében. Ezután a Lagrange-szorzókat frissítjük, és az iteratív folyamatot leállítjuk, ha konvergenciát értünk el. Az iteratív irányított teljes variációfinomítási modell esetében a kiterjesztett Lagrange-módszer az X , P , Q , λ P , λ Q {\displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}} inicializálását jelenti.

.
Itt, H , V , P , Q {\displaystyle H,V,P,Q}

újonnan bevezetett változók, ahol H {\displaystyle H}

= ∇ d h {\displaystyle \nabla d_{h}}

, V {\displaystyle V}

= ∇ d v {\displaystyle \nabla d_{v}}

, P {\displaystyle P}

= ∇ X {\displaystyle \nabla \mathrm {X} }

, és Q {\displaystyle Q}

= P ∙ d {\displaystyle P\bullet d}

. λ H , λ V , λ P , λ Q {\displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}}

a H , V , P , Q {\displaystyle H,V,P,Q}} Lagrange szorzói.

. Minden egyes iterációhoz az L 2 közelítő minimalizálója {\displaystyle L_{2}}

a változók ( X , P , Q {\displaystyle \mathrm {X} ,P,Q}} tekintetében.

) kiszámítása. És ahogy a mezőfinomítási modellben is, a Lagrange-szorzókat frissítjük, és az iteratív folyamatot leállítjuk, ha konvergenciát értünk el.
Az orientációs mező finomítási modell esetében a Lagrange-szorzókat az iteratív folyamat során az alábbiak szerint frissítjük:
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) {\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {\displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k})}

Az iteratív irányított teljes variáció finomítási modell esetében a Lagrange-szorzókat a következőképpen frissítjük:
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}(P^{k}-\nabla (\mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) {\displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}\bullet d)}

Itt, γ H , γ V , γ P , γ Q {\displaystyle \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}

pozitív konstansok.
Előnyei és hátrányai
A teljesítmény teszteléséhez használt csúcsjel-zaj arány (PSNR) és strukturális hasonlósági index (SSIM) metrikák, valamint ismert alaptörvény-képek alapján megállapítható, hogy az iteratív irányított teljes variáció jobb rekonstrukciós teljesítményt nyújt az él- és textúraterületek megőrzésében, mint a nem iteratív módszerek. Az orientációs mező finomítási modellje nagy szerepet játszik ebben a teljesítményjavulásban, mivel növeli az irány nélküli pixelek számát a sík területen, miközben fokozza az orientációs mező konzisztenciáját az élekkel rendelkező régiókban.