Sűríthetőségi tényező (gázok)

Szerző:
A Knowino
Ez az oldal ellenőrzött változata

Ugrás ide:

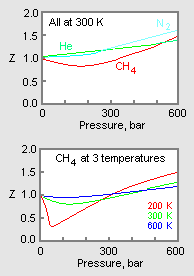
1. ábra: A gázok összenyomhatósági tényezőinek példadiagramjai

Az összenyomhatósági tényező (Z) hasznos termodinamikai tulajdonság az ideális gáztörvény módosítására, hogy figyelembe vegye a valós gázok viselkedését. Azt méri, hogy egy valós gáz termodinamikai tulajdonságai mennyire térnek el az ideális gáztól elvártaktól. Úgy lehet elképzelni, mint a valós gáz tényleges térfogatának és az ideális gáz által a tényleges térfogattal azonos hőmérsékleten és nyomáson megjósolt térfogatnak az arányát.

Az ideális gáz esetében a Z értéke mindig 1. A valós gázok esetében az érték pozitív vagy negatív irányban is eltérhet, a gáz intermolekuláris erőinek hatásától függően. Minél közelebb van egy valós gáz a kritikus pontjához vagy a telítési pontjához, annál nagyobbak a gáz eltérései az ideális viselkedéstől.

Az 1. ábra felső ábrája azt mutatja, hogyan változik a kompresszibilitási tényező különböző gázok esetében azonos hőmérsékleten és nyomáson. Az alsó grafikon azt szemlélteti, hogyan változik egy gáz (például metán) összenyomhatósági tényezője adott nyomáson a hőmérséklet függvényében.

Ez a cikk csak a gázok összenyomhatósági tényezőjével foglalkozik, és nem tér ki a folyadékok vagy gőz-folyadék keverékek összenyomhatóságára.

  • 1 A gázok összenyomhatósági értékeinek meghatározása
    • 1.1 Általánosított összenyomhatósági tényező grafikonok tiszta gázokra
    • 1.2 Általánosított összenyomhatósági tényező grafikonok gázkeverékekre
    • 1.3 A van der Waals-egyenlet
      • 1.3.1 A van der Waals-egyenlet módosított változatai
        • 1.3.1.1 Redlich-Kwong
        • 1.3.1.2 Soave-Redlich-Kwong
        • 1.3.1.3 Peng-Robinson
    • 1.4 Viriális állapotegyenlet
    • 1.5 Egyéb állapotegyenletek
    • 1.6 A gázállandó jelölése
  • 2 Hivatkozások

Gázok összenyomhatósági értékeinek meghatározása

Az ideális gáztörvényt a következőképpen határozzuk meg:

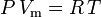
P\,V_\mathrm{m} = R\,T

és a nem-idealitással korrigált ideális gáztörvény meghatározása:

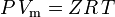
P\,V_\mathrm{m} = ZR\,T

hol:
P = nyomás
Vm = a gáz moláris térfogata
Z =. összenyomhatósági tényező
R = egyetemes gázállandó
T = hőmérséklet

és így:

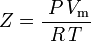
Z = \frac{\;P\,V_\mathrm{m}}{R\,T}

ami a legegyszerűbb és legszélesebb körben használt valós gázállapotegyenlet (EOS). Ennek az állapotegyenletnek a fő korlátja, hogy a gáz összenyomhatósági tényezője, Z, nem állandó, hanem gázonként, valamint a vizsgált gáz hőmérsékletével és nyomásával változik. Kísérleti úton kell meghatározni.

Ahol kísérleti adatok állnak rendelkezésre bizonyos gázokra vonatkozóan, ezek az adatok felhasználhatók a Z és a nyomás függvényében állandó hőmérsékleten, vagy a Z és a nyomás függvényében különböző hőmérsékleteken az adott gázokra vonatkozó grafikonok készítéséhez (mint például az 1. ábrán). Az ilyen grafikonok hasznosak ahhoz, hogy könnyen megkapjuk a Z interpolált értékeit a kísérletileg meghatározott értékek között.

A kompresszibilitási tényező, mint már említettük, a következőképpen is kifejezhető:

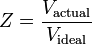
Z = \frac{V_\mathrm{tényleges}}{V_\mathrm{ideális}}

A kompresszibilitási tényezőt három rezsim befolyásolja:

  1. a Z értéke 1 felé tendál, ahogy a gáznyomás közelít a 0-hoz, ahol minden gáz az ideális viselkedés felé tendál
  2. a Z értéke köztes nyomáson kisebb, mint 1, mert a molekulák közötti vonzóerők miatt a tényleges térfogatok kisebbek, mint az ideális értékek
  3. a Z értéke nagyobb, mint 1, és végül a végtelen felé tendál. nagy nyomáson azért, mert a molekulák közötti taszítóerők miatt a tényleges térfogatok nagyobbak az ideális értékeknél

Tiszta gázok általánosított összenyomhatósági tényező grafikonjai

Az összenyomhatósági tényező és a redukált hőmérséklet közötti egyedi összefüggés, Tr, és a redukált nyomás, Pr, közötti kapcsolatot először van der Waals ismerte fel 1873-ban, és a megfelelő állapotok kétparaméteres elve néven ismert. A megfelelő állapotok elve azt az általánosítást fejezi ki, hogy egy gáznak a molekulák közötti erőktől függő tulajdonságai univerzális módon kapcsolódnak a gáz kritikus tulajdonságaihoz. Ez biztosítja a legfontosabb alapot a molekuláris tulajdonságok összefüggéseinek kidolgozásához.

A gázok összenyomhatóságát illetően a megfelelő állapotok elve azt jelzi, hogy bármely tiszta gáznak azonos csökkentett hőmérsékleten, Tr, és azonos csökkentett nyomáson, Pr, azonos összenyomhatósági tényezővel kell rendelkeznie.

A redukált hőmérsékletet és nyomást a következőképpen határozzuk meg:

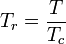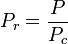
T_r = \frac{T}{T_c}ésP_r = \frac{P}{P_c}

Tc és Pc a gáz kritikus hőmérsékletének és kritikus nyomásának nevezzük. Ezek az egyes gázok jellemzői: Tc az a hőmérséklet, amely felett nem lehet egy adott gázt cseppfolyósítani, Pc pedig az a minimális nyomás, amely egy adott gáz cseppfolyósításához szükséges a kritikus hőmérsékleten. Együttesen határozzák meg egy folyadék kritikus pontját, amely felett az adott folyadék különböző folyékony és gázfázisai nem léteznek.

A valós gázok nyomás-térfogat-hőmérséklet (PVT) adatai tiszta gázonként eltérőek. Ha azonban a különböző egykomponensű gázok összenyomhatósági tényezőit a nyomás függvényében ábrázoljuk a hőmérséklet-izotermákkal együtt (ahogy az 1. ábra alsó ábráján a metán esetében látható), sok grafikon hasonló izoterma-alakot mutat.

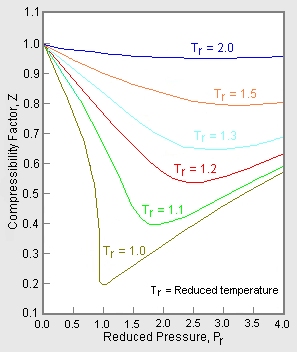
2. ábra: Példa egy általánosított összenyomhatósági tényező grafikonra

Azért, hogy egy olyan általánosított grafikont kapjunk, amely sok különböző gáz esetében használható, a csökkentett nyomást és hőmérsékletet, Pr és Tr, használjuk az összenyomhatósági tényező adatainak normalizálására. A 2. ábra egy példa 10 tiszta gáz, nevezetesen metán, etán, etilén, propán, n-bután, i-pentán, n-hexán, nitrogén, szén-dioxid és gőz több száz kísérleti P-V-T adatpontjából levezetett általánosított összenyomhatósági tényező grafikonjára.

Léteznek részletesebb, általánosított, akár 25 vagy több különböző tiszta gázon alapuló összenyomhatósági tényező grafikonok, mint például a Nelson-Obert grafikonok. Az ilyen grafikonok pontossága állítólag 1-2 százalékon belül van 0,6-nál nagyobb Z értékek esetén, és 4-6 százalékon belül 0,3-0,6 Z értékek esetén.

Az általánosított összenyomhatósági tényező grafikonok jelentősen hibásak lehetnek az erősen poláris gázok esetében, amelyek olyan gázok, amelyeknél a pozitív és negatív töltésközpontok nem esnek egybe. Ilyen esetekben a Z becslése akár 15-20 százalékkal is hibás lehet.

A hidrogén, a hélium és a neon kvantumgázok nem felelnek meg a megfelelő állapotok viselkedésének, és e három gáz redukált nyomását és hőmérsékletét a következő módon kell újra meghatározni, hogy az általánosított grafikonok használata esetén javuljon a kompresszibilitási tényezőik előrejelzésének pontossága:

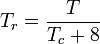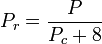
T_r = \frac{T}{T_c + 8}ésP_r = \frac{P}{P_c + 8}

ahol a hőmérsékleteket Kelvin fokban, a nyomásokat pedig atmoszférában adjuk meg.

Általánosított összenyomhatósági tényező grafikonok gázkeverékekre

A tiszta gázokra vonatkozó általánosított összenyomhatósági tényező grafikonok (mint például a 2. ábra vagy a Nelson-Obert grafikonok) gázkeverékekre is használhatók a W. B. Kay által 1936-ban javasolt Kay-szabály alkalmazásával. Ez a szabály egy gázkeverék P-V-T viselkedését úgy jósolja meg, hogy meghatározza a gázkeverék összenyomhatósági tényezőjét csökkentett hőmérsékleten és csökkentett nyomáson, amelyet az álkritikus hőmérséklet, Tpc és az álkritikus nyomás, Ppc alapján határoznak meg, amelyeket a következőképpen határoznak meg:

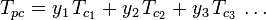
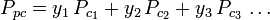
T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_2} + y_3\,T_{c_3}\,\dotsP_{pc} = y_1\,P_{c_1} + y_2\,P_{c_2} + y_3\,P_{c_3}\,\dots

.

hol:
Tpc = a gázelegy pszeudokritikus hőmérséklete
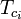T_{c_i} = a gázelegy valamely komponensének kritikus hőmérséklete
Ppc = a pszeudokritikus hőmérséklet. gázelegy nyomása
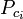P_{c_i} = a gáz egyik komponensének kritikus hőmérséklete
yi = a gáz egyik komponensének mol (vagy térfogat) hányadosa

A pszeudoredukált hőmérséklet, Tpr, és az álredukált nyomás, Ppr, a tiszta gázok általános kompresszibilitási tényezőjének grafikonjaihoz a következők:

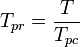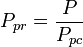
T_{pr} = \frac{T}{T_{pc}}}ésP_{pr} = \frac{P}{P_{pc}}}

A földgázra (amely szénhidrogén és más gázok keveréke) vonatkozó összenyomhatósági tényező grafikon az interneten elérhető pszeudoredukált hőmérséklet és nyomás használatával.

A van der Waals-egyenlet

A van der Waals-egyenletet 1873-ban dolgozták ki, és a következőképpen fejezhető ki:

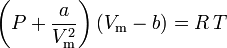
\left(P + \frac{a}{V_\mathrm{m}^2}\right)\left(V_\mathrm{m} - b\right) = R\,T

hol:

a a gázmolekulák közötti vonzás erősségének mértékegysége b a gázmolekulák által elfoglalt térfogatot veszi figyelembe, ami csökkenti a rendelkezésre álló nyitott térfogatot

A van der Waals-egyenlet átrendezhető a következőképpen:

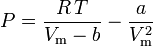
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}

és az összenyomhatósági tényező a következőképpen írható fel:

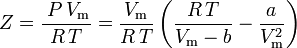
Z = \frac{\;P\,V_\mathrm{m}}{R\,T} = \frac{V_\mathrm{m}}{R\,T}\left(\frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2}\right)

és most már van egy egyenletünk Z meghatározására az a és b van der Waals paraméterek segítségével:

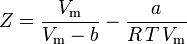
Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}

Bár a-t és b-t “Van der Waals-állandónak” nevezzük, ezek nem valódi állandók, mert gázonként változnak; viszont függetlenek a P, V és T értékektől. Más szóval, a vizsgált gázra nézve állandóak. Egy adott gáz kritikus hőmérsékletének és nyomásának ismeretében a és b az adott gázra az alábbi egyenletekből kapható:

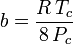
a = \frac{27\, R^2\, T_c^2}{64\, P_c}ésb = \frac{R\, T_c}{8\, P_c}

Például az etán kritikus nyomása 4-es.884 MPa, a kritikus hőmérséklet pedig 305,43 K (32,3˚C). Az R 8,3145 Pa m3 K-1 mol-1 egyetemes gázállandóval számolva a fenti egyenletekből a = 0,557 m6 Pa mol-2 és b = 6,500×10-5 m3 mol-1.

Az a és b táblázatos értékei különböző gázokra az említett hivatkozásokban, valamint a szakirodalom számos más forrásában megtalálhatók.

A van der Waals-egyenlet módosított változatai

A kompresszibilitási tényezőknek a van der Waals-állapotegyenlet segítségével történő meghatározása előrelépés az általánosított kompresszibilitási táblázatok használatával szemben. Vannak azonban a van der Waals-állapotegyenletnek olyan módosított változatai, amelyek még nagyobb javulást biztosítanak. A kőolaj-finomítás, a petrolkémiai termelés, a földgázfeldolgozás, a kriogén desztilláció és a kapcsolódó iparágak területén dolgozó mérnökök által talán leggyakrabban használt állapotegyenletek a következők: az 1949-ben kifejlesztett Redlich-Kwong-egyenlet, az 1972-ben kifejlesztett Soave-Redlich-Kwong-egyenlet és az 1976-ban kifejlesztett Peng-Robinson-egyenlet. Ez a három egyenlet lényegében a van der Waals-egyenlet módosított változata. Az összehasonlító egyenletek a következők:

Redlich-Kwong

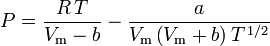
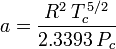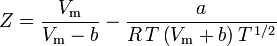
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)T^{\,1/2}}}a = \frac{R^2\, T_c^{\,5/2}}{2.3393\, P_c}ésb = \frac{R\, T_c}{11.5420\, P_c}Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{\,1/2}}

Soave-Redlich-Kwong

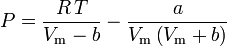
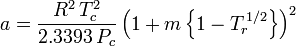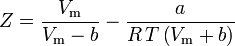
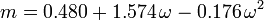
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)}a = \frac{R^2\,T_c^2}{2.3393\,P_c}\, \Big(1 + m\, \Big\{1 - T_r^{\,1/2} \Big\} \Big)^2ésb = \frac{R\, T_c}{11.5420\, P_c}Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)}m = 0.480 + 1,574\, \omega - 0,176\, \omega^2

A Soave-Redlich-Kwong és a Peng-Robinson egyenletekben paraméterként használt akcentrikus tényezőt, ω-t először Pitzer és társai vezették be 1955-ben. A következőképpen fejezhető ki:

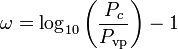
\omega = \log_{10} \left(\frac{P_c}{P_\mathrm{vp}}}\right) - 1

ahol Pvp a gáz telített gőznyomása 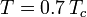T = 0,7\, T_c hőmérsékleten.

Peng-Robinson

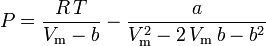
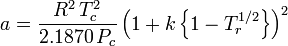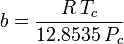
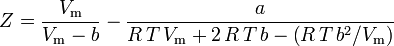
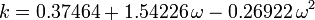
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}\, b - b^2}a = \frac{R^2\,T_c^2}{2.1870\,P_c}\, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big)^2ésb = \frac{R\, T_c}{12.8535\, P_c}Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}} + 2\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)}k = 0,37464 + 1,54226\, \omega - 0,26922\, \omega^2

Viriális állapotegyenlet

A legalapvetőbb állapotegyenlet , mivel a legmegalapozottabb elméleti alapokkal rendelkezik, a viriális állapotegyenlet:

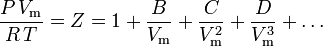
\frac{P\,V_\mathrm{m}}{R\,T} = Z = 1 + \frac{B}{V_\mathrm{m}} + \frac{C}{V_\mathrm{m}^2} + \frac{D}{V_\mathrm{m}^3} + \dots

Először 1885-ben Thiesen javasolta empirikus alapon, majd 1901-ben Kamerlingh-Onnes fejlesztette tovább. A B-re vonatkozó statisztikai-mechanikai kifejezést először Ornstein vezette le doktori disszertációjában. Az egyenletet később 1927-ben H.D. Ursell fejlesztette tovább a molekulák közötti erők statisztikai-mechanikai (klaszteres) elemzéséből származó elméleti alapon.

A B, C és D paramétereket második, harmadik és negyedik viriális együtthatónak nevezzük. Az együtthatók nem konstansok, mivel gázonként, valamint a vizsgált gáz hőmérsékletétől függően változnak. Néha B(T), C(T) és D(T) alakban írjuk őket, hogy jelezzük, hogy a hőmérséklet függvényei. Az együtthatók számszerű értékét kísérletileg kell meghatározni.

A második viriális együttható adja a gáz nem ideális viselkedésére vonatkozó korrekció legnagyobb részét. Emiatt a virialis egyenletet néha a második együtthatót tartalmazó kifejezés után csonkolják. Ha azonban a harmadik együttható is rendelkezésre áll, az egyenletet általában a harmadik együtthatót tartalmazó kifejezés után vágják le. A negyedik együttható ritkán áll rendelkezésre.

A tiszta gázokra és gázkeverékekre vonatkozó viriális együtthatók átfogó összeállítását a korábban a Texas A&M University, College Station, Texas, jelenleg pedig a National Institute of Standards and Technology (NIST), Boulder, Colorado székhelyén működő Termodinamikai Kutatóközpont viriális együttható adatbázisából készítették el. Ennek az összeállításnak a legutóbbi változatát 2003-ban tették közzé. A NIST megvásárolható egy szoftverprogram is, a NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), amely tartalmazza a második és harmadik viriális együtthatókat, valamint számos más termodinamikai tulajdonságot.

Egyéb állapotegyenletek

A valós gázok viselkedésének előrejelzésére számos más állapotegyenlet is létezik. Talán a legismertebbek az 1929-ben kidolgozott Beattie-Bridgeman-egyenlet és az 1940-ben kidolgozott Benedict-Rubin-Webb-egyenlet. Ezek általában bonyolultabbak, mint a fent tárgyalt egyenletek.

A gázállandó jelölése

Az ebben a cikkben használt gázállandó az univerzális gázállandó, R, amely minden gázra érvényes. Létezik egy fajlagos gázállandó is, amelyet Rs-ként jelölhetünk, és a következő módon definiálható: Rs = R / M, ahol M a molekulatömeg.

Sajnos a szakirodalomban sok szerző néha az R-t használja fajlagos gázállandóként anélkül, hogy ezt így jelölné, vagy jelezné, hogy ez a fajlagos gázállandó. Ez félreértéshez vezethet és vezet is.

  1. 1,0 1,1 1,2 1,3 1,4 McQuarrie, Donald A. és Simon, John D. (1999). Molekuláris termodinamika. University Science Books. ISBN 1-891389-05-X.
  2. 2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal és Robert H. Turner (2004). A termál-áramlástan alapjai, 2. kiadás. McGraw-Hill Professional. ISBN 0-07-245426-1.
  3. 3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Bevezetés a vegyészmérnöki termodinamikába, hetedik kiadás. McGraw Hill. ISBN 0-07-310445-0.
  4. 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Vegyészmérnöki termodinamika. Universities Press (India). ISBN 81-7371-048-1.
  5. 5.0 5.1 Gáztörvények (M.J. Mombourquette professzor előadása a kanadai Queens Egyetemen)
  6. Hong Wei Xiang (2005). A megfelelő állapotok elve és annak gyakorlata: Folyadékok termodinamikai, transzport és felületi tulajdonságai. Elsevier. ISBN 0-444-52062-7.
  7. IUPAC Goldbook
  8. Gouq-Jen Su (1946). “A megfelelő állapotok módosított törvénye”. Ipari & Mérnöki kémia 38 (8): 803-806. ISSN 0096-4484.
  9. 9.0 9.1 Állapotegyenletek (Lyes Kadem professzor, Concordia Egyetem, Kanada)
  10. 10.0 10.1 Állapotegyenletek (Sanford Klein professzor előadásának anyaga, Wisconsin-Madison Egyetem, USA)
  11. Richard W. Miller (1996). Áramlásmérési mérnöki kézikönyv, 3. kiadás. McGraw-Hill. ISBN 0-07-042366-0. (Lásd a G-1 ábrát a G.145. oldalon)
  12. Kai-Fui Vincent Wong (2000). Termodinamika mérnököknek, 1. kiadás. CRC Press. ISBN 0-8493-0232-3. (Lásd A-2. ábra, 278. oldal}
  13. Nelson-Obert általánosított összenyomhatósági diagramok (Az interneten elérhető diagramok, a San Diego State University, U.S. honlapjáról)
  14. W.B.Kay (1936). “Gázok és gőzök magas hőmérsékleten és nyomáson – A szénhidrogén sűrűsége”. Industrial Engineering & Chemistry 28:1014. ISSN 0096-4484.
  15. Yunus A. Çengal és Michael A. Bowes (2005). Termodinamika: An Engineering Approach, 5. kiadás. McGraw-Hill. ISBN 0-07-2884959.
  16. Valódi gázok (R.M. Price professzor előadásának anyaga a Christian Brothers University-n, U.S.A.)
  17. A természetes gázok tulajdonságai (Jon Steiner Gudmandsson professzor, Norvég Tudományos és Technológiai Egyetem)
  18. Robert C. Weast (szerkesztő) (1975). A kémia és fizika kézikönyve, 56. kiadás. CRC Press. ISBN 0-87819-455-X.
  19. 19.0 19.1 19.2 Chapter 3: Equations of State (pages 6-8 of 65 pdf pages) (Part of PhD dissertation by Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)
  20. 20.0 20.1 20.2 Jean Vidal (2003). Termodinamika: Alkalmazások a vegyiparban és a kőolajiparban. Editions Technip. ISBN 2-7108-0800-5.
  21. Zakia Nasri és Housam Binous (2007). “A Soave-Redlich-Kwong állapotegyenlet alkalmazásai a Mathematica segítségével”. Journal of Chemical Engineering of Japan 40 (6): 534-538. Letölthető innen.
  22. K.S. Pitzer et al (1955). “A folyadékok térfogati és termodinamikai tulajdonságai”. Journal of the American Chemical Society 77: 3427-3440.
  23. Francis S. Manning és Richard E. Thompson (1991). A kőolaj olajmezei feldolgozása. Pennwell Books. ISBN 0-87814-343-2.
  24. Acentric Factor Definition (Physical Property Sources Index, PPSI, of the Swiss Federal Institute of Technology Zurich)
  25. Max F. Thiesen (1885). “Vizsgálatok az állapotegyenletről”. Annalen der Physik und Chemie (24): 467-492.
  26. Heike Kamerlingh-Onnes (1901). “A gázok és folyadékok állapotegyenletének kifejezése sorozatok segítségével”. Commun. Phys. Lab. Leiden (71).
  27. S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Gibbs statisztikai mechanikájának alkalmazása molekulaelméleti problémákra), Leiden
  28. H. D. Ursell (1927). “A Gibbs-féle fázisintegrál kiértékelése tökéletlen gázok esetében” (23): 685.
  29. J. D. Dymond és R. C. Wilhoit (szerzők), K. N. Marsch és M. Fenkel (szerkesztők) (2003). Tiszta gázok és keverékek viriális együtthatói, 1. kiadás. Springer. ISBN 3-540-44340-1.
  30. NIST Standard Reference Database 23
  31. J.A. Beattie és O.C. Bridgeman (1929). “A New Equation of State for Fluids” (Egy új állapotegyenlet a folyadékokra). Proc. Amer. Acad. Arts Sci. (63): 229-305.
  32. M. Benedict, G.B. Webb és L.C. Rubin (1940). “An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures”. J. Chem. Phys. 8: 334-335.
Information.svg Az oldal egyes tartalmai korábban már megjelentek a Citizendiumon.
Az “http://knowino.org/wiki/Compressibility_factor_(gases)”
kategóriából letöltve: Fizika

Kategória: Fizika

Szólj hozzá!