A cellás automata “színes” cellák gyűjteménye egy meghatározott alakú rácson, amely a szomszédos cellák állapotán alapuló szabályrendszer szerint diszkrét időlépéseken keresztül fejlődik. A szabályokat aztán iteratív módon, tetszőleges számú időlépésre alkalmazzuk. von Neumann volt az egyik első, aki ilyen modellel foglalkozott, és cellás modellt épített be az “univerzális konstruktorába”. A sejtautomatákat az 1950-es évek elején tanulmányozták a biológiai rendszerek lehetséges modelljeként (Wolfram 2002, 48. o.). A celluláris automaták átfogó tanulmányozását az 1980-as évektől kezdve S. Wolfram végezte, és Wolfram alapvető kutatásai ezen a területen A New Kind of Science (Wolfram 2002) című könyvének megjelenésében csúcsosodtak ki, amelyben Wolfram az automatákkal kapcsolatos eredmények gigantikus gyűjteményét mutatja be, amelyek között számos úttörő új felfedezés található.
A NUMB3RS című televíziós bűnügyi dráma 2. évadának “Fogadó vagy rosszabb” című epizódja (2006) említi az egydimenziós celluláris automatákat.
A celluláris automatáknak számos formája és fajtája létezik. A cellás automaták egyik legalapvetőbb tulajdonsága az, hogy milyen típusú rácson számolnak. A legegyszerűbb ilyen “rács” egy egydimenziós vonal. Két dimenzióban négyzet, háromszög és hatszög alakú rácsok is szóba jöhetnek. A cellás automaták tetszőleges számú dimenziójú kartéziánus rácsokon is konstruálhatók, a 
dimenziós egész számok rácsa a legelterjedtebb választás. A 
-dimenziós egész számrácson lévő celluláris automatákat a Wolfram Nyelvben CellularAutomaton néven implementálják.
A színek (vagy különböző állapotok) 
számát is meg kell adni, amit egy celluláris automata felvehet. Ez a szám jellemzően egész szám, a 
(bináris) a legegyszerűbb választás. Egy bináris automata esetében a 0 színt általában “fehérnek”, az 1 színt pedig “feketének” nevezik. Azonban a lehetséges értékek folytonos tartományával rendelkező cellás automaták is szóba jöhetnek.
Amellett, hogy milyen rácson él egy cellás automata, és milyen színeket vehetnek fel a cellái, azt a szomszédságot is meg kell adni, amelyben a cellák egymásra hatnak. A legegyszerűbb választás a “legközelebbi szomszédok”, amelyben minden egyes időlépésnél csak az adott cellával közvetlenül szomszédos cellák lehetnek hatással. Két gyakori szomszédság egy négyzetrácson álló kétdimenziós cellás automata esetében az úgynevezett Moore-negyed (négyzet alakú szomszédság) és a von Neumann-negyed (rombusz alakú szomszédság).
A cellás automaták legegyszerűbb típusa a bináris, legközelebbi szomszédos, egydimenziós automata. Az ilyen automatákat S. Wolfram “elemi celluláris automatáknak” nevezte el, aki részletesen tanulmányozta csodálatos tulajdonságaikat (Wolfram 1983; 2002, 57. o.). 256 ilyen automata létezik, amelyek mindegyike egy egyedi bináris számmal indexelhető, amelynek decimális ábrázolása az adott automata “szabályaként” ismert. A 30-as szabály illusztrációja a fenti ábrán látható az általa egyetlen fekete cellából kiindulva 15 lépés után létrehozott evolúcióval együtt.
A cellás automaták egy kissé bonyolultabb osztálya a legközelebbi szomszédos, 
színű, egydimenziós totalisztikus cellás automaták. Az ilyen automatákban a szomszédos cellák átlaga határozza meg a fejlődést, és a legegyszerűbb nem triviális példák 
színűek. Az ilyen automaták esetében a viselkedést leíró szabályok halmaza kódolható egy 
-jegyű 
-jegyű számként, úgynevezett “kódként”. A terner (
) kódú 912-es automata szabályai és 300 lépése a fenti ábrán látható.
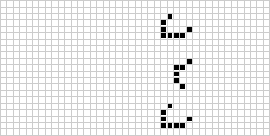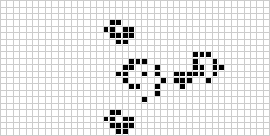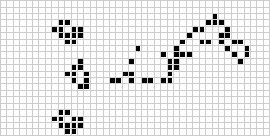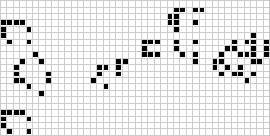
Két dimenzióban a legismertebb cellás automata a Conway-féle életjáték, amelyet J. H. Conway fedezett fel 1970-ben, és Martin Gardner a Scientific American hasábjain népszerűsített. Az élet játéka egy bináris (
) totalisztikus cellás automata, amelynek Moore-környéke 
tartományú. Bár az életjáték egymást követő generációinak kiszámítását eredetileg kézzel végezték, a számítógépes forradalom hamarosan megérkezett, és lehetővé tette a kiterjedtebb minták tanulmányozását és szaporítását. A puffer train néven ismert életjáték-konstrukció animációja a fenti ábrán látható.
A WireWorld egy másik elterjedt kétdimenziós cellás automata.
A cellás automaták elmélete rendkívül gazdag, mivel egyszerű szabályok és struktúrák is képesek váratlan viselkedések nagy változatosságát produkálni. Léteznek például univerzális cellás automaták, amelyek képesek bármely más cellás automata vagy Turing-gép viselkedését szimulálni. Gacs (2001) még azt is bebizonyította, hogy léteznek hibatűrő univerzális cellás automaták, amelyeknek más cellás automaták szimulálására való képességét nem akadályozzák véletlenszerű perturbációk, feltéve, hogy az ilyen perturbációk kellően ritkák.