Barycentrische Coördinaten

door
Meetkunde > CoördinatenGeometrie >
Meetkunde > Vlakke Meetkunde > Driehoeken > Driehoekseigenschappen >

Barycentrische coördinaten zijn drievoudige getallen (t_1,t_2,t_3) corresponderend met massa’s geplaatst op de hoekpunten van een referentiedriehoek DeltaA_1A_2A_3. Deze massa’s bepalen dan een punt P, dat het meetkundig zwaartepunt is van de drie massa’s en dat geïdentificeerd wordt met coördinaten (t_1,t_2,t_3). De hoekpunten van de driehoek zijn gegeven door (1,0,0), (0,1,0), en (0,0,1). Barycentrische coördinaten werden in 1827 door Möbius ontdekt (Coxeter 1969, blz. 217; Fauvel et al. 1993).

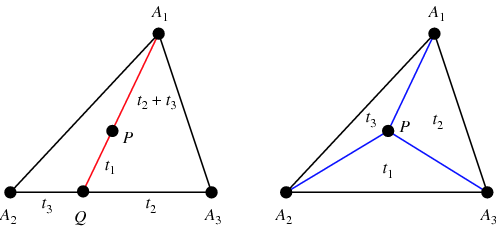
Barycentric

Om de barycentrische coördinaten te vinden voor een willekeurig punt P, vindt men t_2 en t_3 vanaf het punt Q op het snijpunt van de lijn A_1P met de zijde A_2A_3, en bepaal dan t_1 als de massa op A_1 die een massa t_2+t_3 op Q in evenwicht zal brengen, waardoor P het zwaartepunt wordt (linker figuur). Verder zijn de oppervlakten van de driehoeken DeltaA_1A_2P, DeltaA_1A_3P, en DeltaA_2A_3P evenredig met de barycentrische coördinaten t_3, t_2, en t_1 van P (rechter figuur; Coxeter 1969, p. 217).

Barycentrische coördinaten zijn homogeen, dus

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

voor mu!=0.

Barycentrische coördinaten die zo genormaliseerd zijn dat ze de werkelijke oppervlakten van de deelhoeken worden, worden homogene barycentrische coördinaten genoemd. Barycentrische coördinaten genormaliseerd zodat

t_1+t_2+t_3=1,
(2)

zodat de coördinaten de oppervlakten van de subtriangels geven genormaliseerd naar de oppervlakte van de oorspronkelijke driehoek heten areale coördinaten (Coxeter 1969, p. 218). Barycentrische en areale coördinaten kunnen bijzonder elegante bewijzen opleveren van meetkundige stellingen zoals de stelling van Routh, de stelling van Ceva en de stelling van Menelaus (Coxeter 1969, pp. 219-221).

(Niet noodzakelijk homogene) barycentrische coördinaten voor een aantal veel voorkomende middelpunten zijn samengevat in de volgende tabel. In de tabel zijn a, b, en c de zijlengtes van de driehoek en s de halve omtrek.

driehoeksmiddelpunt barycentrische coördinaten
omtreksmiddelpunt O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
excenter J_B (a,-b,c)
excenter J_C (a,b,-c)
Gergonne punt Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incenter I (a,b,c)
Nagel punt Na (s-a,s-b,s-c)
orthocentrum H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
symmediaans punt K (a^2,b^2,c^2)
driehoekszwaartepunt G (1,1,1)

In barycentrische coördinaten heeft een lijn een lineaire homogene vergelijking. In het bijzonder, de rechte tussen de punten (r_1,r_2,r_3) en (s_1,s_2,s_3) heeft vergelijking

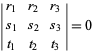|r_1 r_2 r_3; s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 en 57; Coxeter 1969, p. 219; Bottema 1982). Als de hoekpunten P_i van een driehoek DeltaP_1P_2P_3 barycentrische coördinaten (x_i,y_i,z_i) hebben, dan is de oppervlakte van de driehoek

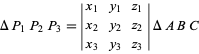DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Plaats een reactie