Dit zijn stochastische leerprocessen met recurrente structuur en liggen aan de basis van de vroege optimalisatietechnieken die in ANN worden gebruikt. De Boltzmann Machine werd in 1985 uitgevonden door Geoffrey Hinton en Terry Sejnowski. Meer duidelijkheid kan worden waargenomen in de woorden van Hinton over de Boltzmann Machine.
“Een verrassend kenmerk van dit netwerk is dat het alleen lokaal beschikbare informatie gebruikt. De verandering van het gewicht hangt alleen af van het gedrag van de twee eenheden die het verbindt, ook al optimaliseert de verandering een globale maatstaf” – Ackley, Hinton 1985.
Enkele belangrijke punten over Boltzmann Machine –
-
Zij maken gebruik van recurrente structuur.
-
Zij bestaan uit stochastische neuronen, die een van de twee mogelijke toestanden hebben, ofwel 1 of 0.
-
Enkele van de neuronen in dit netwerk zijn adaptief (vrije toestand) en andere zijn geklemd (bevroren toestand).
-
Als we gesimuleerde annealing toepassen op discreet Hopfield-netwerk, dan zou het een Boltzmann-machine worden.
Doel van de Boltzmann-machine
Het belangrijkste doel van de Boltzmann-machine is het optimaliseren van de oplossing van een probleem. Het is het werk van Boltzmann Machine om de gewichten en de hoeveelheid met betrekking tot dat bepaalde probleem te optimaliseren.
Architectuur
Het volgende diagram toont de architectuur van Boltzmann machine. Uit het diagram blijkt duidelijk, dat het een tweedimensionale array van eenheden is. Hier zijn de gewichten van de onderlinge verbindingen tussen de eenheden -p, waarbij p > 0. De gewichten van de zelfverbindingen worden gegeven door b, waarbij b > 0.
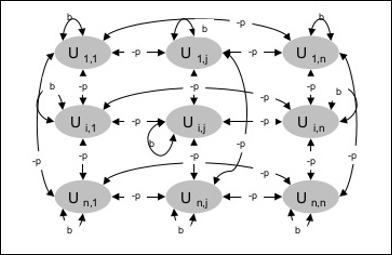
Trainingsalgoritme
Zoals we weten hebben Boltzmann-machines vaste gewichten, zodat er geen trainingsalgoritme is, omdat we de gewichten in het netwerk niet hoeven bij te werken. Om het netwerk te testen moeten we echter de gewichten instellen en de consensusfunctie (CF) vinden.
De Boltzmann-machine heeft een verzameling eenheden Ui en Uj en heeft tweerichtingsverbindingen op deze eenheden.
-
We beschouwen het vaste gewicht zeg wij.
-
wij ≠ 0 als Ui en Uj verbonden zijn.
-
Er bestaat ook een symmetrie in de gewogen interconnectie, d.w.z.d.w.z. wij = wji.
-
wii bestaat ook, d.w.z. er zou de zelfconnectie tussen eenheden zijn.
-
Voor elke eenheid Ui zou haar toestand ui ofwel 1 ofwel 0 zijn.
Het hoofddoel van de Boltzmann-machine is het maximaliseren van de consensusfunctie (CF), die kan worden gegeven door de volgende relatie
$$CF:=:\displaystyle\sum_limits_{i} \displaystyle\sum_limits_{jj} w_{ij}u_{i}u_{j}$$
Nu, wanneer de toestand verandert van 1 in 0 of van 0 in 1, dan kan de verandering in consensus worden gegeven door de volgende relatie –
$\Delta CF:=(1:-2u_{i})(w_{ij}:+:vertoningsstijl_sum_limieten_{jj} u_{i} w_{ij})$$
Hierbij is ui de huidige toestand van Ui.
De variatie in de coëfficiënt (1 – 2ui) wordt gegeven door de volgende relatie –
$$(1:-:2u_{i})†:=begin{gevallen}+1, & U_{i}:is:op dit moment:U_{i}:is:momenteel:einde{gevallen}$$
In het algemeen verandert eenheid Ui niet van toestand, maar als zij dat wel doet dan zou de informatie lokaal bij de eenheid blijven. Met die verandering zou ook de consensus van het netwerk toenemen.
De waarschijnlijkheid dat het netwerk de verandering in de toestand van de eenheid aanvaardt, wordt gegeven door de volgende relatie –
$$AF(i,T)\:=:\frac{1}{1:+:exp}$$
Hierbij is T de sturende parameter. Deze neemt af naarmate CF de maximumwaarde bereikt.
Test-algoritme
Stap 1 – Initialiseer het volgende om de training te starten –
- Gewichten die de beperking van het probleem voorstellen
- Controleparameter T
Stap 2 – Ga verder met stap 3-8, wanneer de stopvoorwaarde niet waar is.
Stap 3 – Voer de stappen 4-7 uit.
Stap 4 – Veronderstel dat een van de toestanden het gewicht heeft gewijzigd en kies het gehele getal I, J als willekeurige waarden tussen 1 en n.
Stap 5 – Bereken de verandering in de consensus als volgt –
$$Delta CF:=(1:-:2u_{i})(w_{ij}:+:\displaystyle\sum_limits_{j\neq i} u_{i} w_{ij})$$
Step 6 – Bereken de kans dat dit netwerk de verandering in toestand zou accepteren
$AF(i,T)\:=:\frac{1}{1:+:exp}$$
Stap 7 – Accepteer of weiger deze verandering als volgt –
Geval I – als R < AF, accepteer de verandering.
Geval II – als R ≥ AF, de wijziging verwerpen.
Hierbij is R een willekeurig getal tussen 0 en 1.
Stap 8 – Verlaag de regelparameter (temperatuur) als volgt –
T(nieuw) = 0.95T(oud)
Stap 9 – Test voor de stopcondities die als volgt kunnen zijn –
- De temperatuur bereikt een gespecificeerde waarde
- Er is geen verandering in de toestand gedurende een gespecificeerd aantal iteraties